Возможные ловушки и проблемы: нужно учесть, что основание системы счисления должно быть больше любой цифры числа, поэтому делитель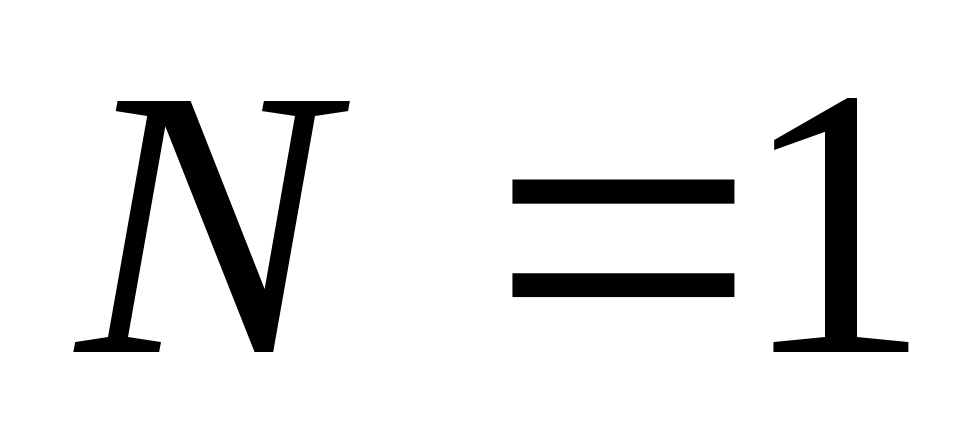 не подходит (должно быть ) числа нужно записывать в ответе в порядке возрастания, как требуется по условию

Решение (программа на Python, А.Н. Носкин):

1. 
   можно решить задачу с помощью программы:
   

for i in range(3,50):# перебираем возможные основания

x = 23 # число по условию

x_N = ''

while x > 0:# перевод в N-ю систему

if x%i>9:break # пропускаем цифры в виде букв

else: x_N += str(x%i)

x //= i

x_N = x_N[::-1]# разворот числа

if x_N == '': pass

elif x_N[-1]== "2":

print(i, end=",")

2. 
   Ответ: 3, 7, 21.
   

Решение (программа на Python, Б.С. Михлин):

3. 
   полная программа:
   

for x in range(3, 22): # x - основание от 3 до 21

# (дальше перебирать нет смысла)

if 23 % x == 2:

print( x, end = ',' )

4. 
   Ответ: 3, 7, 21.
   

---

Еще пример задания:

Р-9. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 11.

Общий подход:

• 
  неизвестно основание системы счисления, мы обозначим его через
  
• 
  пока будем считать, что запись числа 31 в системе с основанием состоит из трех цифр, причем две младшие (11) нам даны, а одну (обозначим ее через ) нужно найти:
  

2 1 0 ← разряды

31 = k 1 1_N = k·N² + N¹ + N⁰ = k·N² + N + 1

• 
  можно показать, что при большем количестве разрядов эта формула также верна, то есть, число 31 можно представить как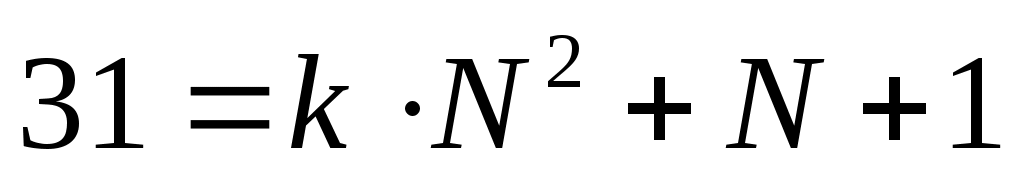 при некотором целом ; например, для числа с пятью разрядами получаем:
  

4 3 2 1 0 ← разряды

31 = k₄ k₃ k₂ 1 1_N = k₄·N⁴ + k₃·N³ + k₂·N² + N¹ + N⁰

= k·N² + N + 1

для (из первых трех слагаемых вынесли общий множитель )

Решение:

1. 
   итак, нужно найти все целые числа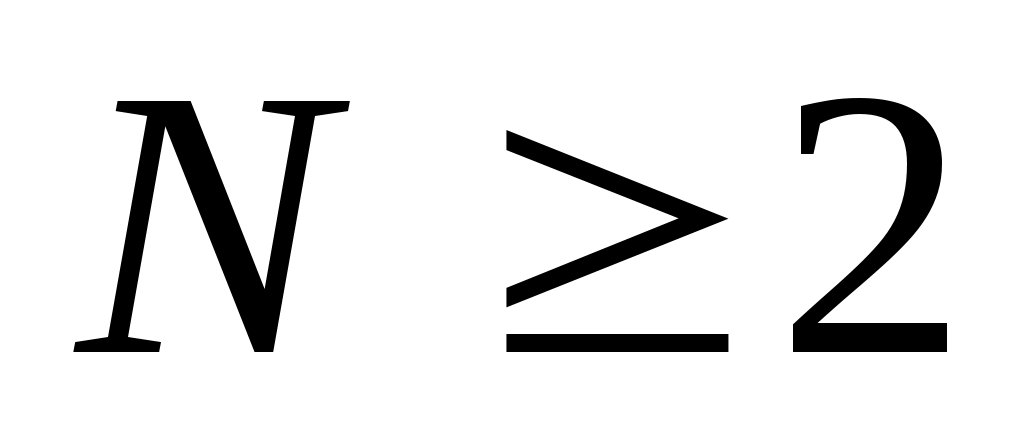 , такие что
   

(**)

где – целое неотрицательное число (0, 1, 2, …);

2. 
   сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
   
3. 
   из формулы (**) получаем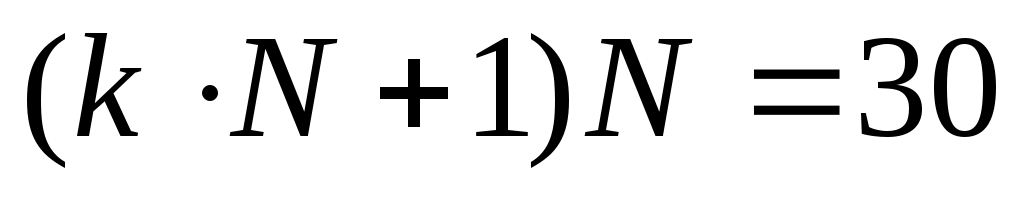 , так что задача сводится к тому, чтобы найти все делители числа 30 и отобрать только те из них, для которых уравнение (**) разрешимо при целом , то есть, 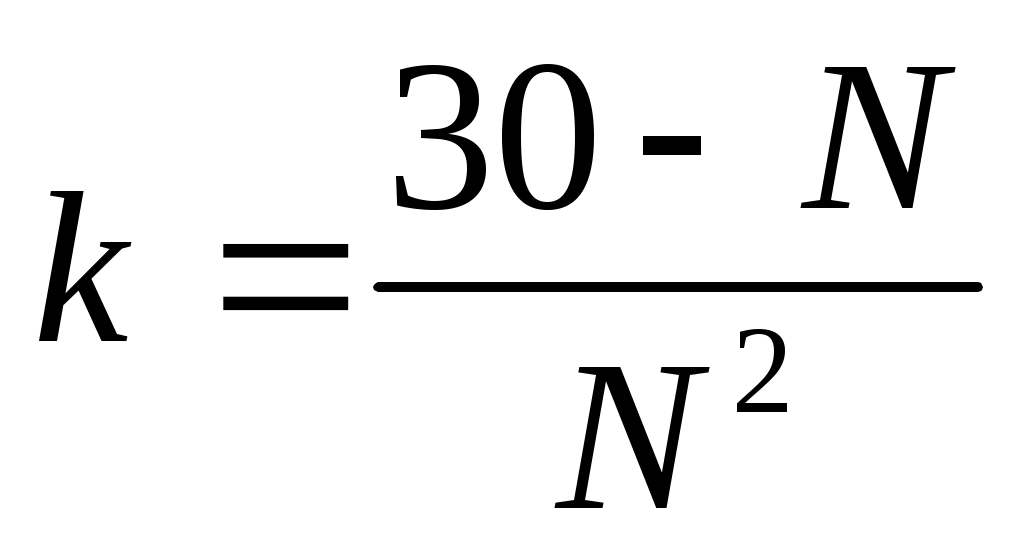– целое число
   
4. 
   выпишем все делители числа 30, большие или равные 2: 2, 3, 5, 6, 10, 15, 30
   
5. 
   из всех этих делителей только для 2, 3, 5 и 30 значение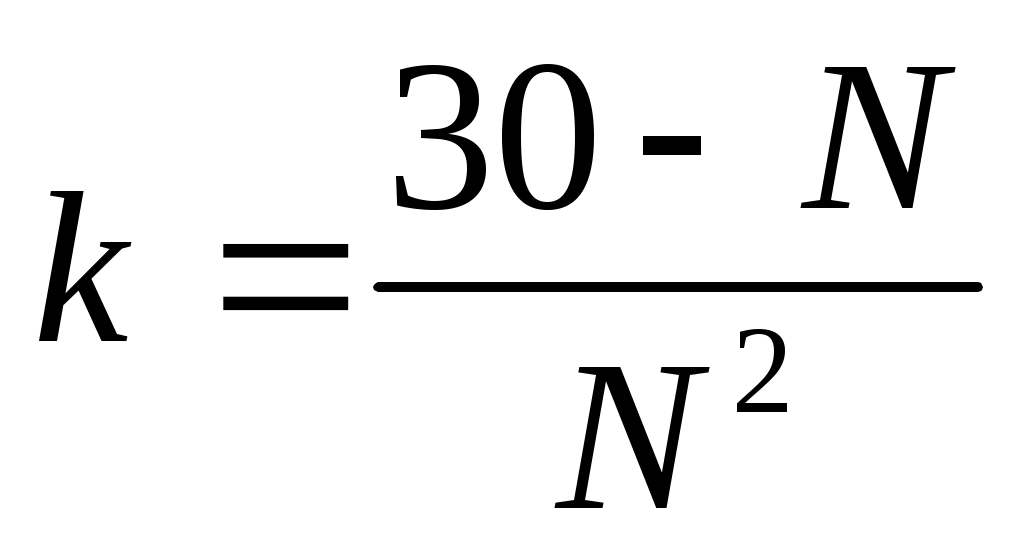 – целое число (оно равно соответственно 7, 3, 1 и 0)
   
6. 
   таким образом, верный ответ – 2, 3, 5, 30.
   

---

Решение (программа на Python, А.Н. Носкин):

1. 
   можно решить задачу с помощью программы:
   

for i in range(3,50):# перебираем возможные основания

x = 23 # число по условию

x_N = ''

while x > 0:# перевод в N-ю систему

if x%i>9:break # пропускаем цифры в виде букв

else: x_N += str(x%i)

x //= i

x_N = x_N[::-1]# разворот числа

if x_N == '': pass

elif x_N[-1]== "2":

print(i, end=",")

2. 
   ответ: 2, 3, 5, 30.
   

Решение (программа на Python, Б.С. Михлин):

5. 
   полная программа:
   

for x in range(2, 101): # x - основание

# справа число 11 переведено в 10-ую систему

if 31 % (x*x) == x + 1:

print( x, end = ',' )

6. 
   Ответ: 2, 3, 5, 30.
   

Еще пример задания:

Р-8. Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12, …, 17 в системе счисления с основанием 5.

Решение (вариант 1):

1. 
   запишем первое и последнее число в заданном диапазоне в системе счисления с основанием 5:
   

10 = 20₅, 17 = 32₅ .

2. 
   заметим, что оба они содержат цифру 2, так что, 2 цифры мы уже нашли
   
3. 
   между 20₅ и 32₅ есть еще числа
   

21₅, 22₅, 23₅, 24₅, 30₅, 31₅.

4. 
   в них 5 цифр 2 (в числе 22₅ – сразу две двойки), поэтому всего цифра 2 встречается 7 раз
   
5. 
   таким образом, верный ответ – 7.
   

Возможные ловушки и проблемы: нужно не забыть, что в системе счисления с основанием 5 старшая цифра – 4, то есть, вслед за 245 следует 305 помните, что нужно определить не количество чисел, в которых есть двойка, а количество самих двоек можно не обратить внимание на то, что в числе 225 цифра 2 встречается 2 раза

Решение (вариант 2):

1. 
   переведем все указанные числа в систему счисления с основанием 5:
   

10 = 20₅, 11 = 21₅, 12 = 22₅, 13 = 23₅, 14 = 24₅, 15 = 30₅, 16 = 31₅, 17 = 32₅ .

2. 
   считаем цифры 2 – получается 7 штук
   
3. 
   таким образом, верный ответ – 7 .
   

Решение (программа на

---

Python, А.Н. Носкин):

1. 
   можно решить задачу с помощью программы:
   

k = 0

for i in range(10,17+1):

x = i

x5 = ''

while x > 0:# перевод в 5-ю систему

x5 += str(x%5)

x //= 5

x5 = x5[::-1]# разворот числа

k += x5.count("2")

print(k)

2. 
   ответ: 7.
   

Решение (программа на Python, Б.С. Михлин):

1. 
   ещё одна программа:
   

k = 0 # счетчик цифр 2

for x in range(10,17+1):

xw = x # xw - рабочая (work) копия x

while xw:

if xw % 5 == 2: # считаем цифры 2 в 5-ой системе

k += 1

xw //= 5

print( k )

2. 
   ответ: 7.
   

Еще пример задания:

Р-7. Укажите наименьшее основание системы счисления, в которой запись числа 30 трехзначна.

Решение:

1. 
   обозначим через неизвестное основание системы счисления, тогда запись числа 30 в этой системе имеет вид
   

2. 
   вспомним алгоритм перевода числа из системы счисления с основанием в десятичную систему: расставляем сверху номера разрядов и умножаем каждую цифру на основание в степени, равной разряду:
   

3. 
   поскольку запись трехзначная,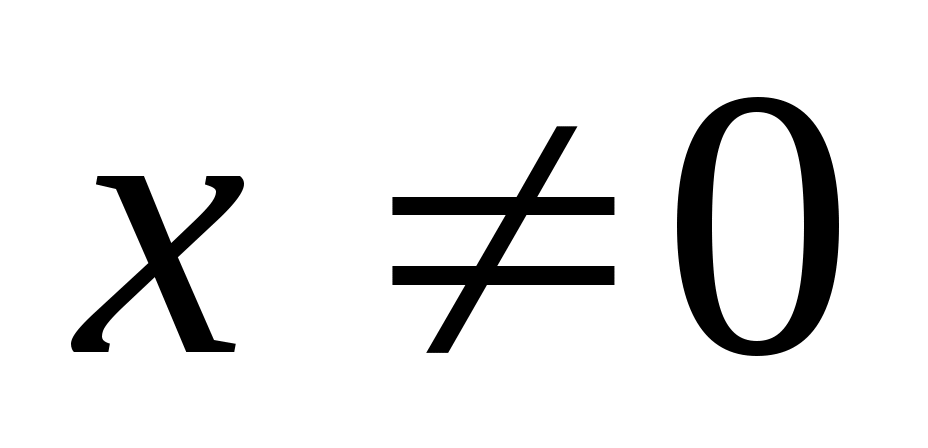 , поэтому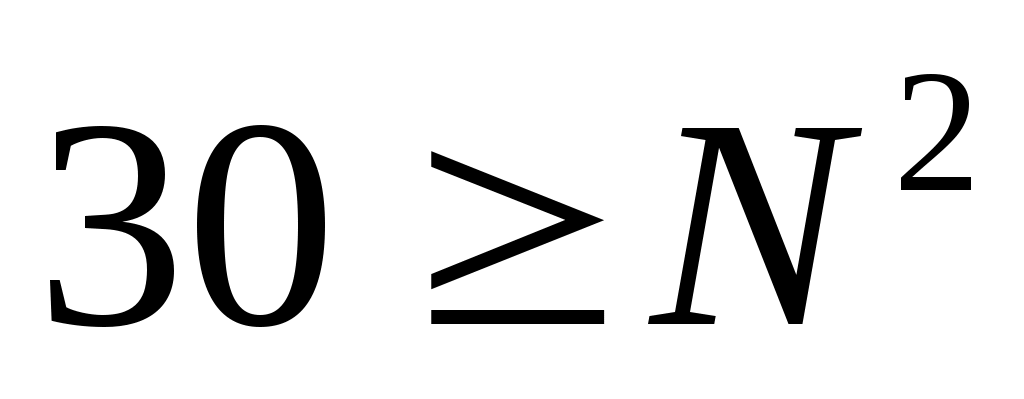
   
4. 
   с другой стороны, четвертой цифры нет, то есть, в третьем разряде – ноль, поэтому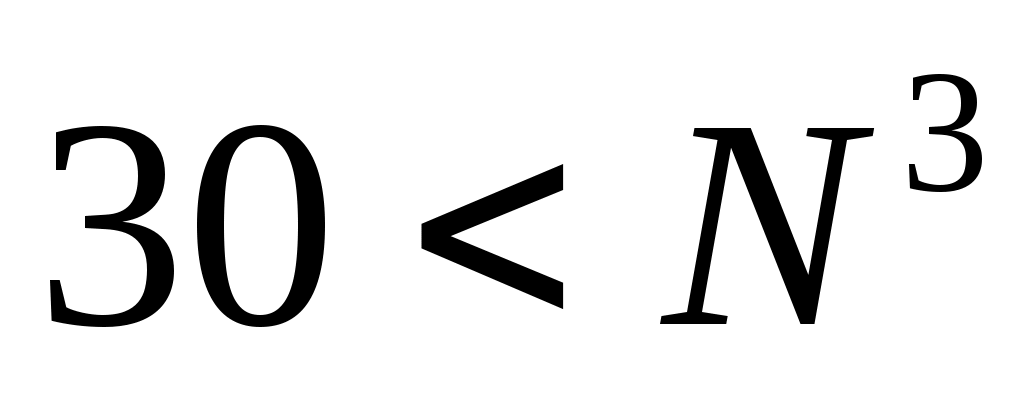
   
5. 
   объединяя последние два условия, получаем, что искомое основание удовлетворяет двойному неравенству
   

6. 
   учитывая, что – целое число, методом подбора находим целые решения этого неравенства; их два – 4 и 5:
   

---

7. 
   минимальное из этих значений – 4
   
8. 
   таким образом, верный ответ – 4 .
   

Решение (без подбора):

1. 
   выполним п.1-4 так же, как и в предыдущем варианте решения
   
2. 
   найдем первое целое число, куб которого больше 30; это 4, так как
   

3. 
   проверяем второе неравенство: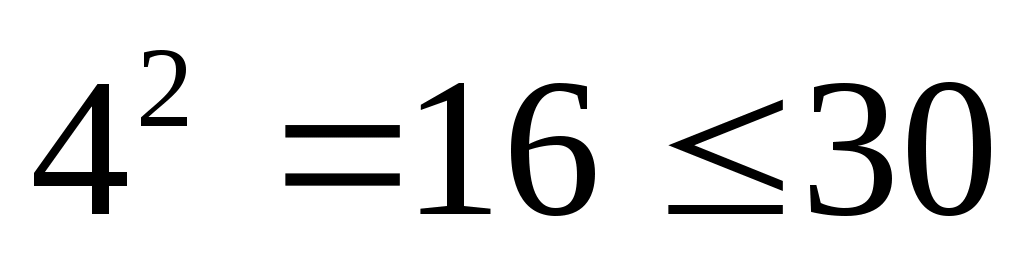 , поэтому в системе счисления с основанием 4 запись числа 30 трехзначна
   
4. 
   таким образом, верный ответ – 4 .
   

Решение (программа на Python, А.Н. Носкин):

1. 
   можно решить задачу с помощью программы:
   

for i in range(2,100):# перебираем возможные основания

x = 30 # число по условию

x_N = ''

while x > 0:# перевод в N-ю систему

x_N += str(x%i)

x //= i

x_N = x_N[::-1]# разворот числа

if len(x_N)== 3:

print(i)

break

2. 
   ответ: 4.
   

Решение (программа на Python, Б.С. Михлин):

7. 
   полная программа:
   

for N in range(2, 10): # проверять основание N >=10 нет смысла

# (будет два или один разряд)

if N ** 2 <= 30 < N ** 3: # проверка на трёхзначность

print(N)

break

8. 
   Ответ: 4.
   

Еще пример задания:

Р-6. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 начинается на 3?

Решение (вариант 1):

1. 
   нас интересуют числа от 1 до 30
   
2. 
   сначала определим, сколько цифр может быть в этих числах, записанных в системе счисления с основанием 5
   
3. 
   поскольку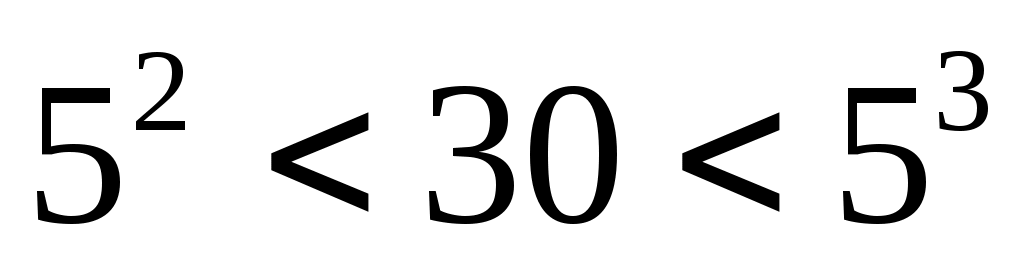 , в интересующих нас числах может быть от 1 до 3 цифр
   
4. 
   рассмотрим трехзначные числа, начинающиеся на 3 в системе с основанием 5:
   

все они заведомо не меньше , поэтому в наш диапазон не попадают;

5. 
   таким образом, остается рассмотреть только однозначные и двухзначные числа
   
6. 
   есть всего одно однозначное число, начинающееся на 3, это 3
   
7. 
   общий вид всех двузначных чисел, начинающихся на 3 в системе с основанием 5:
   

---

Смотрите также файлы

• Дневник производственной практики пм. 04 Выполнение работ по профессии Младшая медицинская сестра по уходу за больными.docx

• Немного предыстории и истории Power bi.pdf

• Противодействие коррупции любых стран.docx

• Сценарий 9 мая 2023 года.docx

• Методические рекомендации по организации выполнения и защиты дипломного проекта (работы) по программам подготовки специалистов среднего звена.docx