ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 1054
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
где
-
используя эту формулу, находим интересующие нас двузначные числа – 15, 16, 17, 18 и 19 -
таким образом, верный ответ – 3, 15, 16, 17, 18, 19 .
Решение (вариант 2, предложен Сенькиной Т.С., г. Комсомольск-на-Амуре ):
-
нас интересуют числа от 1 до 30; сначала определим, сколько цифр может быть в пятеричной записи эти чисел -
поскольку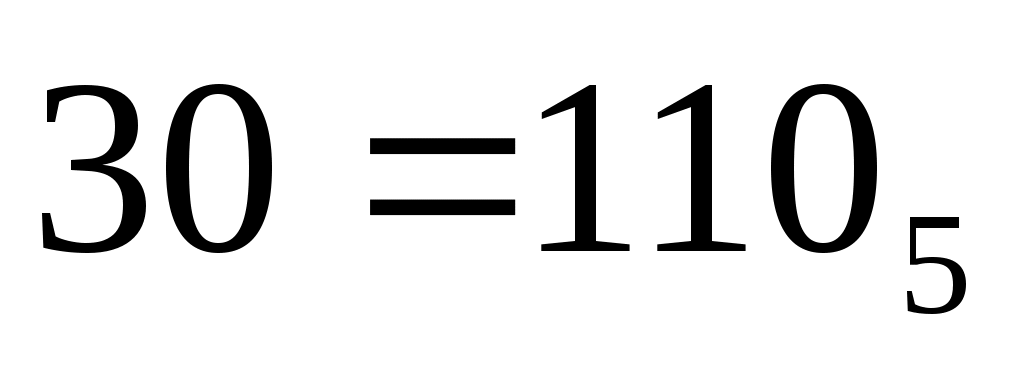 , в интересующих нас числах может быть не более 2 цифр (все трехзначные пятеричные числа, начинающиеся с 3, больше 30)
, в интересующих нас числах может быть не более 2 цифр (все трехзначные пятеричные числа, начинающиеся с 3, больше 30) -
есть всего одно однозначное число, начинающееся на 3, это 3 -
выпишем все пятеричные двузначные числа, которые начинаются с 3, и переведем их в десятичную систему: 305 = 15, 315 = 16, 325 = 17, 335 = 18 и 345 = 19 -
таким образом, верный ответ – 3, 15, 16, 17, 18, 19 .
Решение (программа на Python, А.Н. Носкин):
-
можно решить задачу с помощью программы:
for i in range(1,31):# перебираем ответы
x = i
x5 = ''
while x > 0:# перевод в 5-ю систему
x5 += str(x%5)
x //= 5
x5 = x5[::-1]# разворот числа
if x5[0]== "3":
print(i, end=",")
-
ответ: 3, 15, 16, 17, 18, 19.
Еще пример задания:
Р-05. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.
Решение (1 способ):
-
Если число в системе с основанием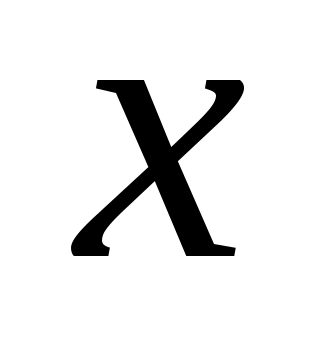 оканчивается на 13, то
оканчивается на 13, то-
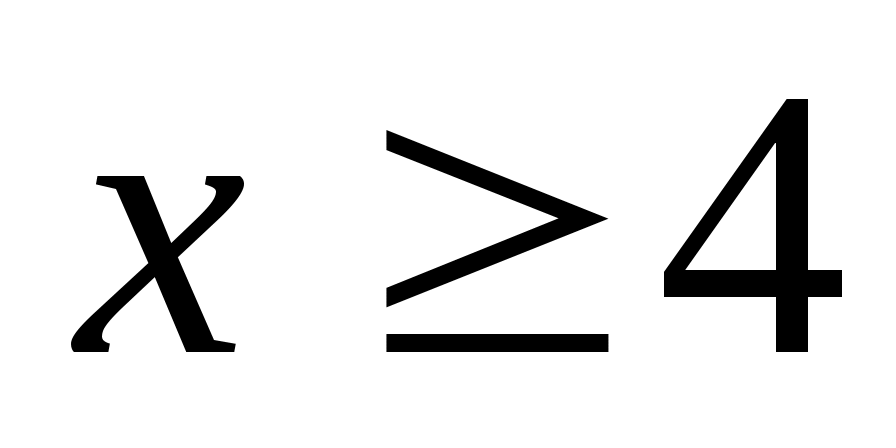 , потому что в системах с меньшим основанием нет цифры 3
, потому что в системах с меньшим основанием нет цифры 3 -
это число можно представить в виде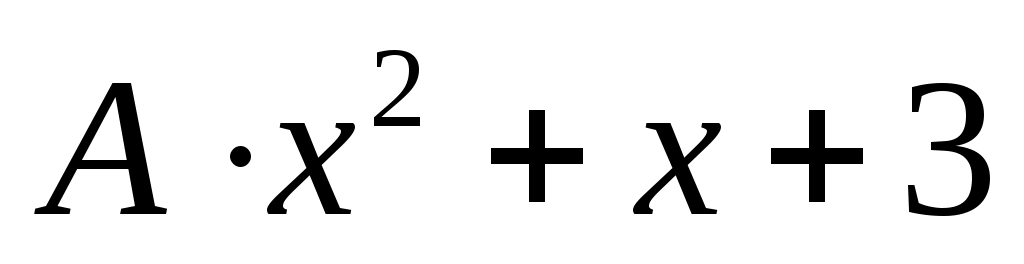 , где
, где  – целое неотрицательное число
– целое неотрицательное число
-
-
определим наибольшее возможное с учетом условия
с учетом условия 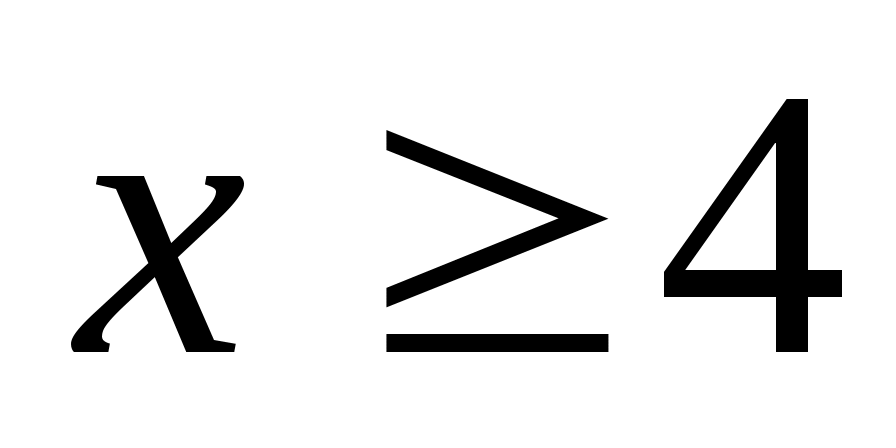 . Из уравнения
. Из уравнения 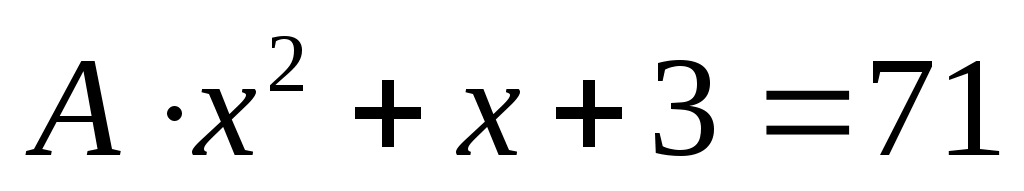 следует
следует 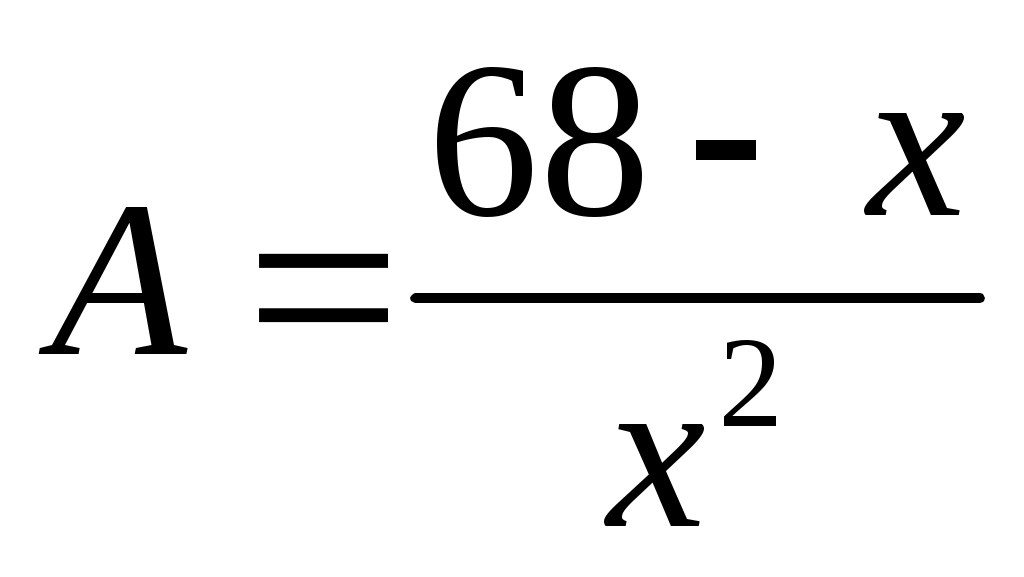 .
. -
очевидно, что чем меньше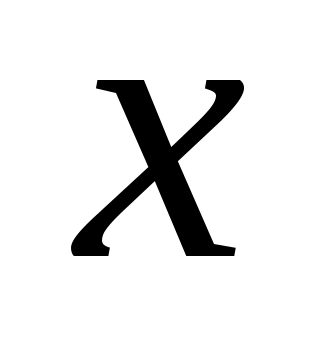 , тем больше
, тем больше  , поэтому значение
, поэтому значение  не превышает
не превышает 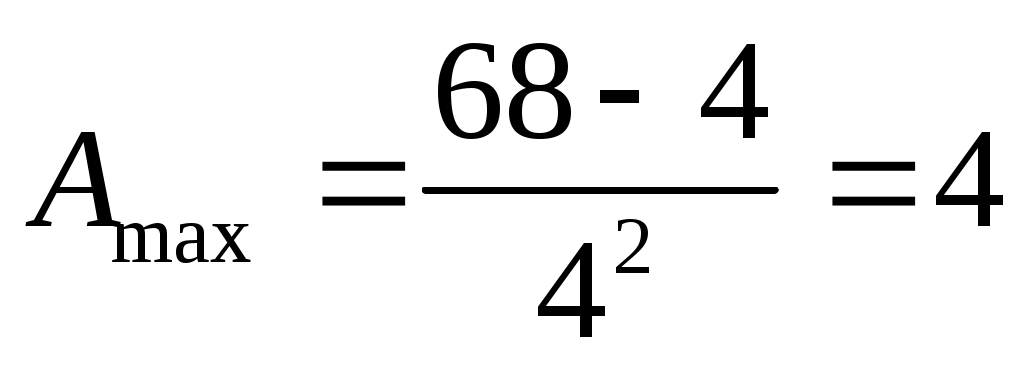
здесь мы подставили
-
остается перебрать все допустимые значения (от 0 до
(от 0 до 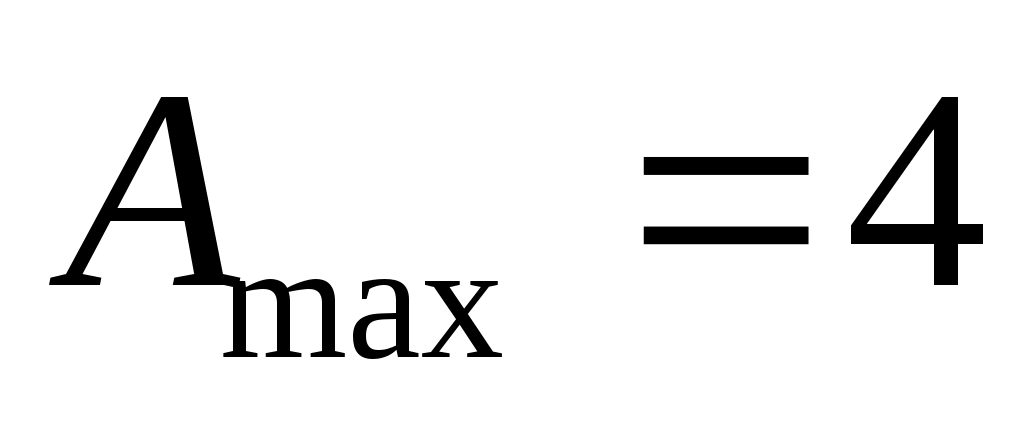 ), решая для каждого из них уравнение
), решая для каждого из них уравнение
относительно
-
получаем-
при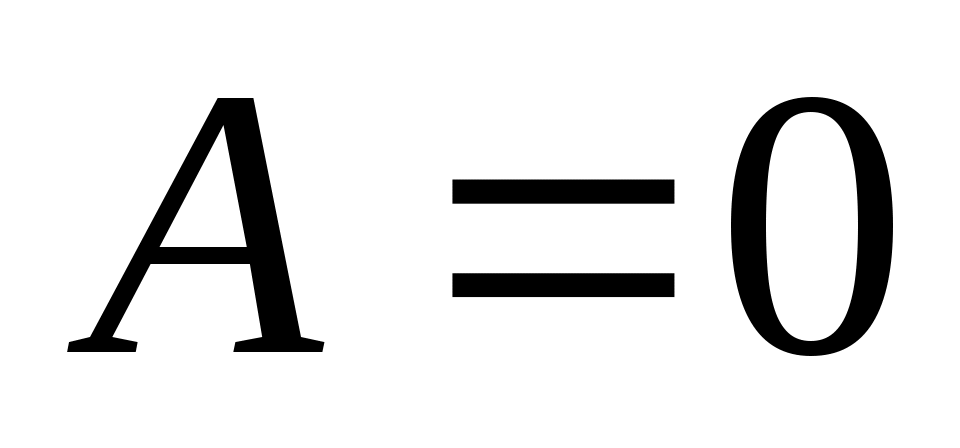 :
: 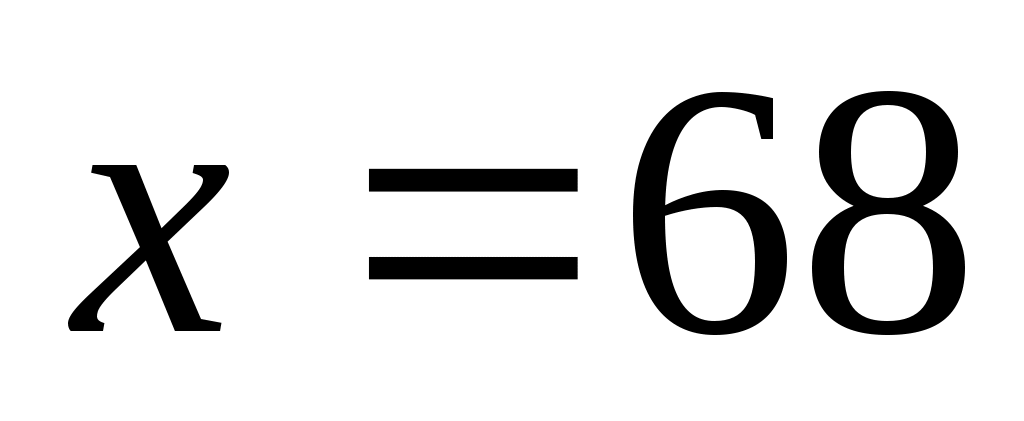
-
при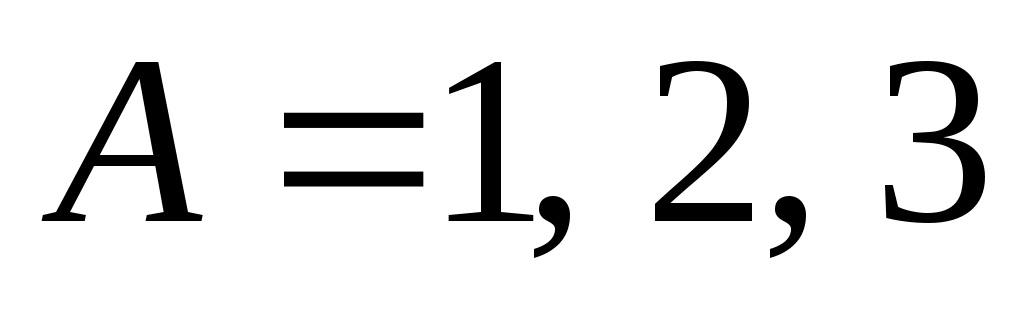 : решения – не целые числа
: решения – не целые числа -
при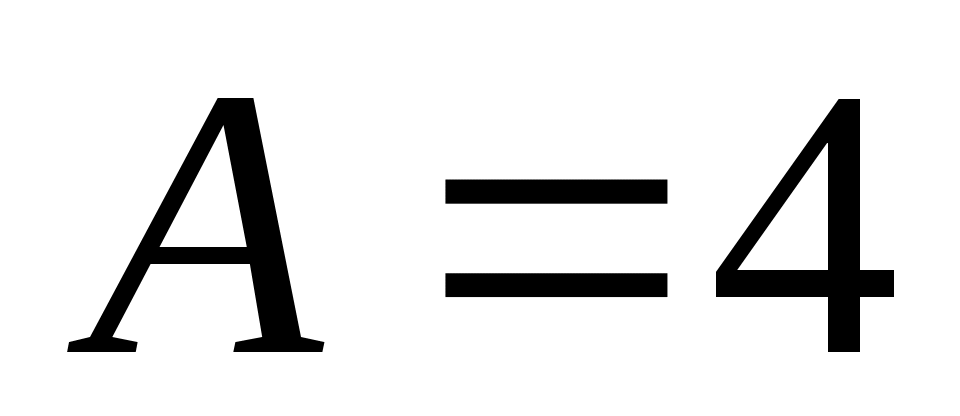 :
: 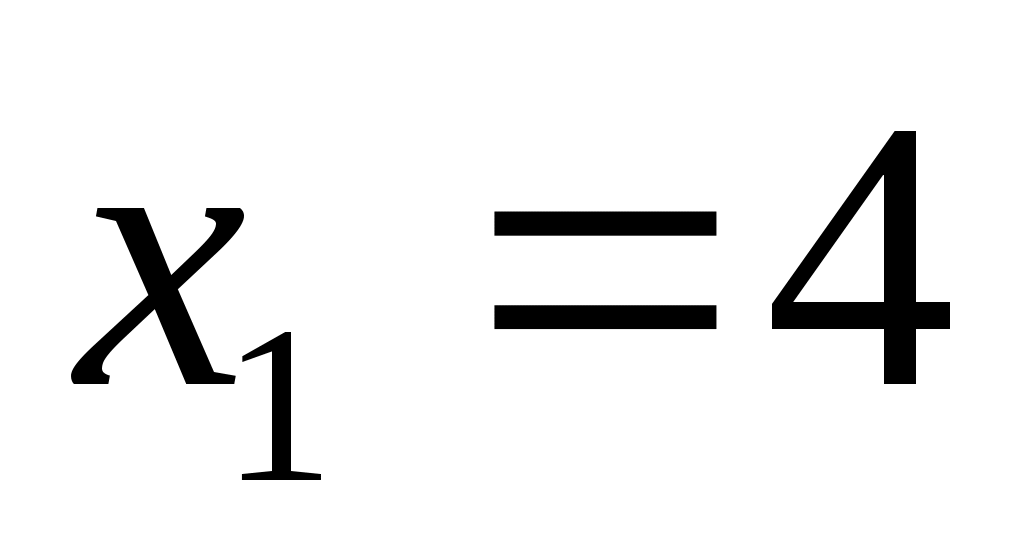 и
и 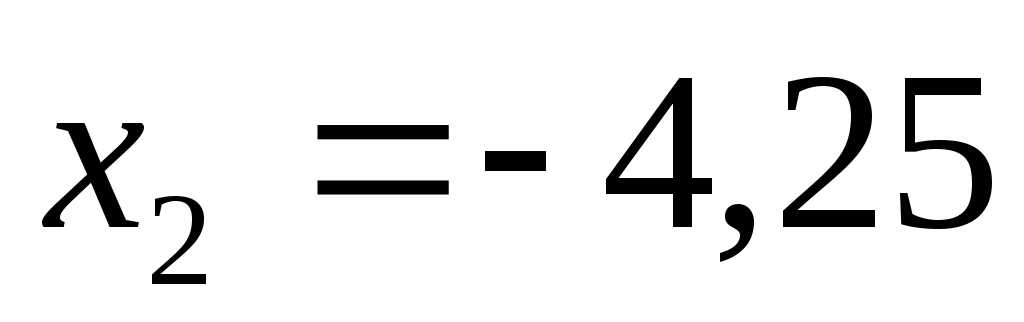 , второе решение не подходит
, второе решение не подходит
-
-
таким образом, верный ответ: 4, 68.
Решение (2 способ, М.В. Кузнецова и её ученики):
-
запись числа71 в системе с основанием оканчивается на 13, т.е. в разряде единиц – 3, это значит, что остаток от деления 71 на
оканчивается на 13, т.е. в разряде единиц – 3, это значит, что остаток от деления 71 на  равен 3, то есть для некоторого целого
равен 3, то есть для некоторого целого имеем
имеем
-
таким образом, искомые основания – делители числа 68; остается выбрать из них те, которые соответствуют другим условиям задачи -
среди чисел, оканчивающихся на 13 в системе счисления с основанием ,минимальное – это само число
,минимальное – это само число 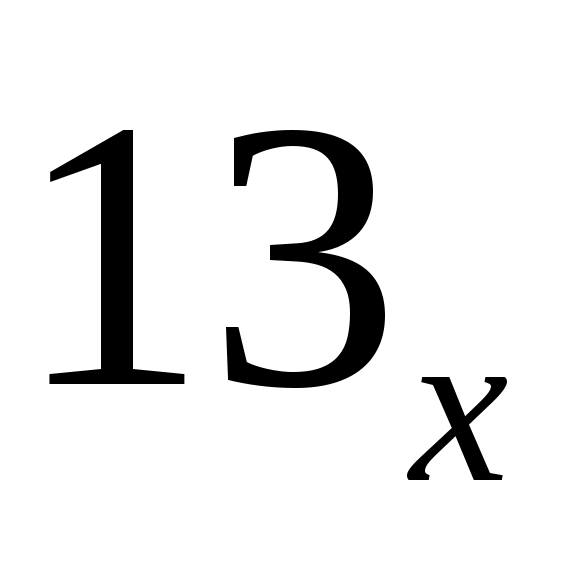 ; отсюда найдем максимальное основание:
; отсюда найдем максимальное основание:
так что первый ответ: 68.
-
остальные числа, окачивающиеся в этой системе на 13, имеют не менее 3-х знаков (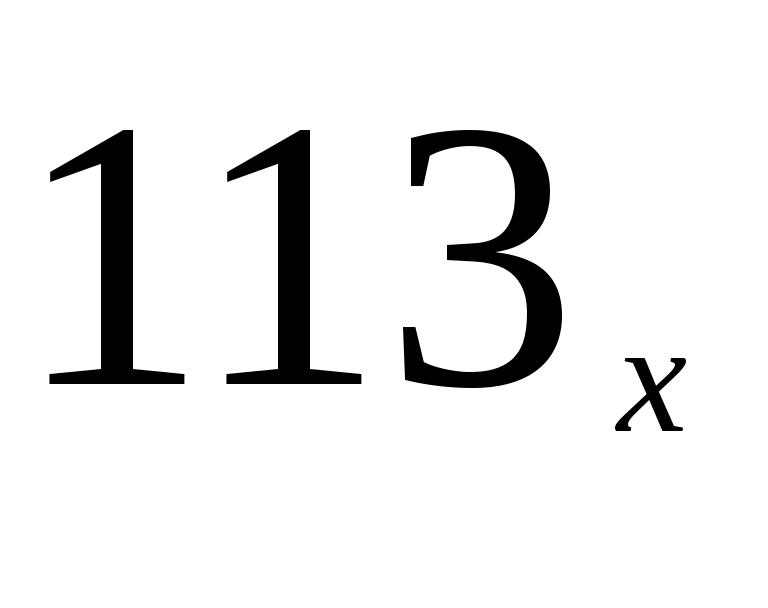 ,
,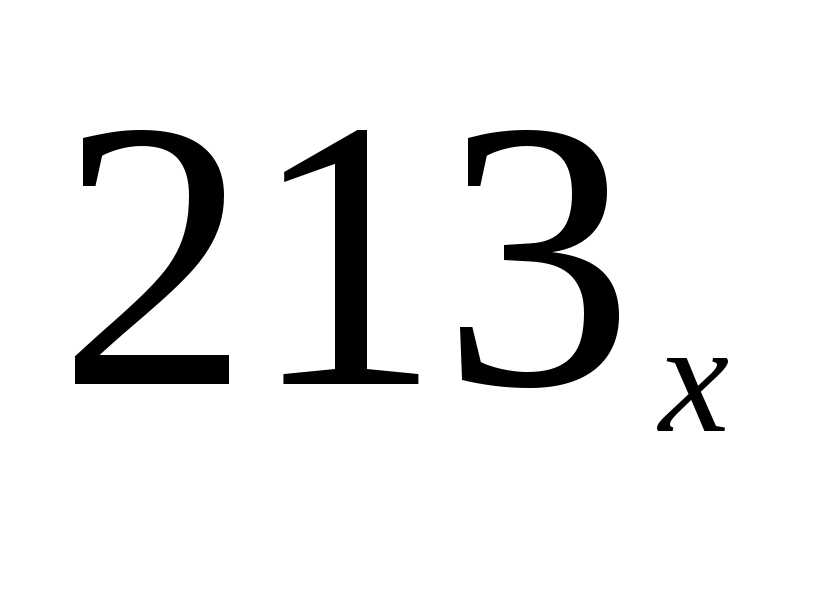 …), т.е. все они больше
…), т.е. все они больше 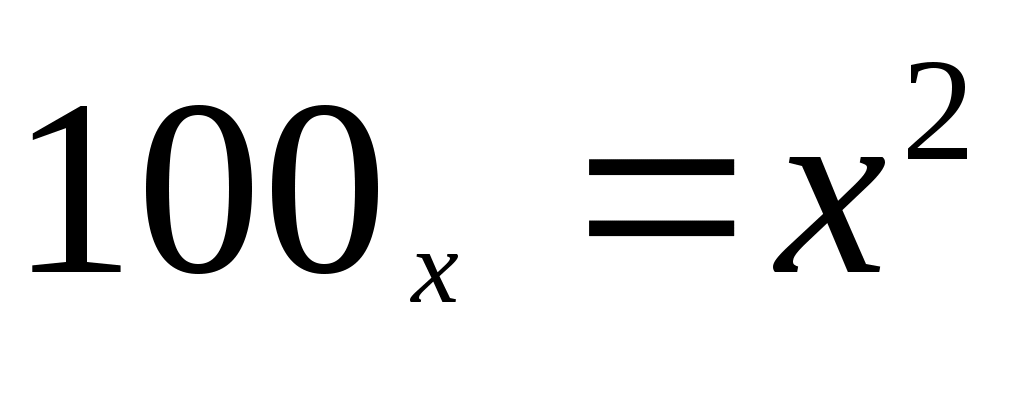
-
поэтому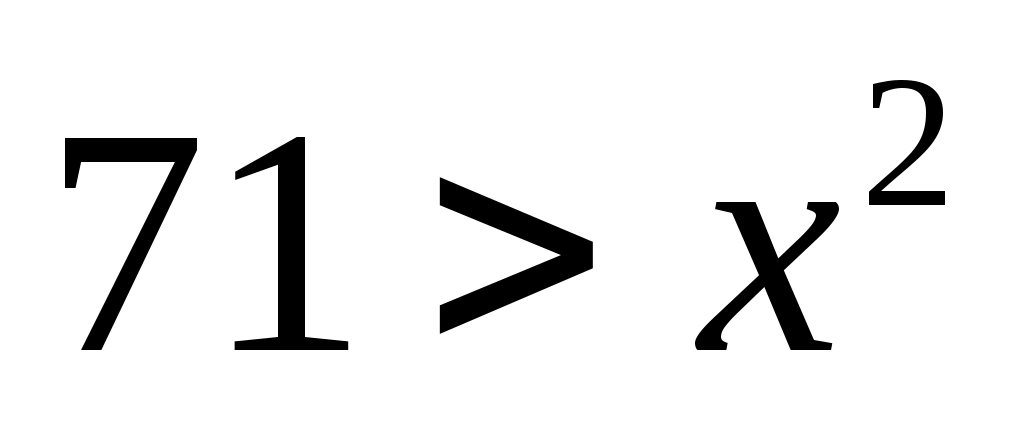 , следовательно,
, следовательно, 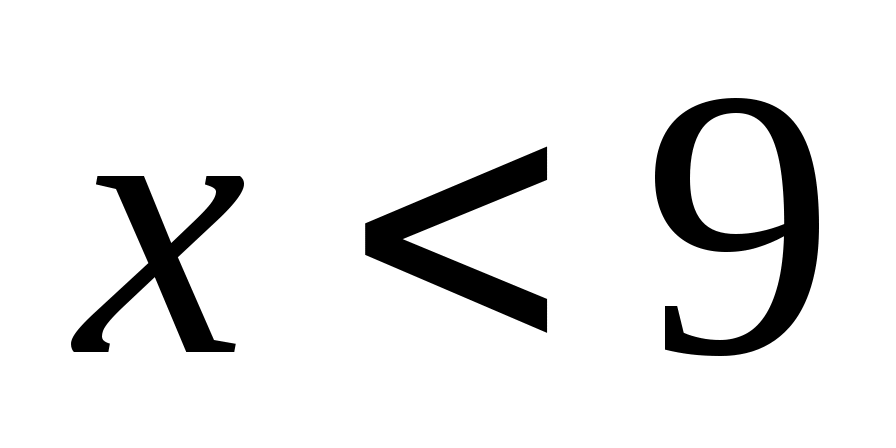
-
по условию в записи числа есть цифра 3, поэтому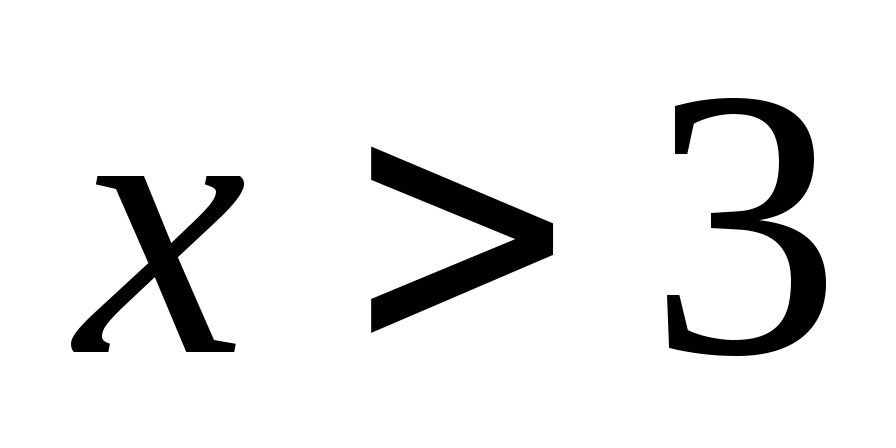 (в системах с основанием 3 цифры 3 нет)
(в системах с основанием 3 цифры 3 нет) -
итак: , и при этом
, и при этом  – делитель 68; единственное возможное значение
– делитель 68; единственное возможное значение 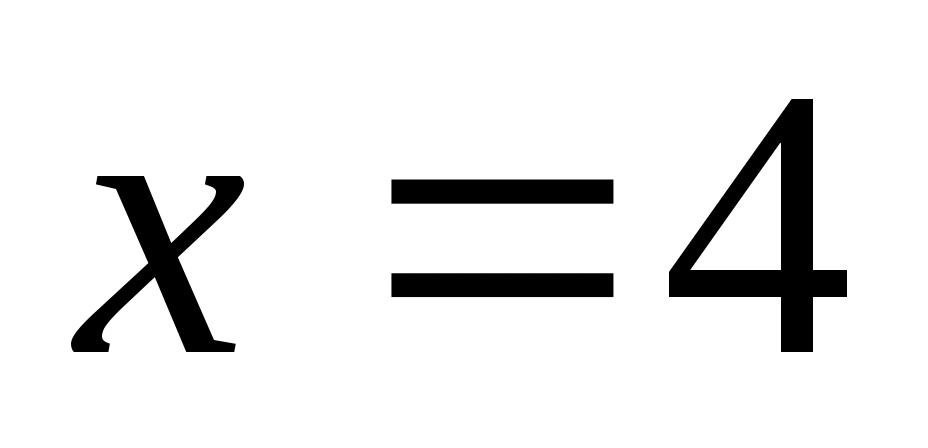 (на 5,6,7 и 8 число 68 не делится)
(на 5,6,7 и 8 число 68 не делится) -
таким образом, верный ответ: 4, 68.
-
Возможные ловушки и проблемы:-
на шаге 1 нужно вычесть из числа только число единиц, то есть младшую из двух заданных цифр (в примере – 3) -
можно забыть рассмотреть двузначное число, записанное заданными в условии цифрами (в примере – 13x ), и пропустить максимальное основание -
нужно помнить, что
-
максимальная цифра на 1 меньше основания системы счисления -
100 в системе с основанием p равно p2
-
Решение (программа на Python, А.Н. Носкин):
-
можно решить задачу с помощью программы:
for i in range(4,100):# перебираем возможные основания
x = 71 # число по условию
x_N = ''
while x > 0:# перевод в N-ю систему
if x%i>9:break # пропускаем цифры в виде букв
else: x_N += str(x%i)
x //= i
x_N = x_N[::-1]# разворот числа
if x_N[-2:]== "13":
print(i, end=",")
-
ответ: 4, 68.
Решение (программа на
Python, Б.С. Михлин):
-
полная программа:
for x in range(4, 72): # x - основание от 4 до 71
# (дальше перебирать нет смысла)
# справа число 13 переведено в 10-ую систему
if 71 % (x*x) == x + 3:
print( x, end = ',' )
-
Ответ: 4, 68.
Еще пример задания:
Р-04. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 86 оканчивается на 22.
Решение (1 способ):
-
Если число в системе с основанием оканчивается на 22, то
оканчивается на 22, то-
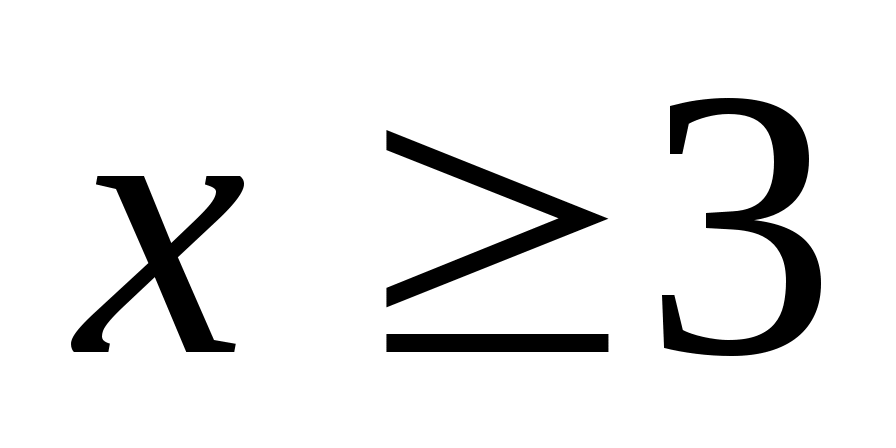 , потому что в системах с меньшим основанием нет цифры 2
, потому что в системах с меньшим основанием нет цифры 2 -
это число можно представить в виде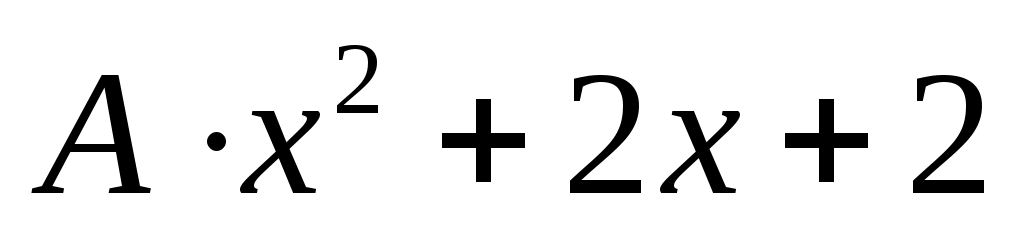 , где
, где  – целое неотрицательное число
– целое неотрицательное число
-
-
определим наибольшее возможное с учетом условия
с учетом условия 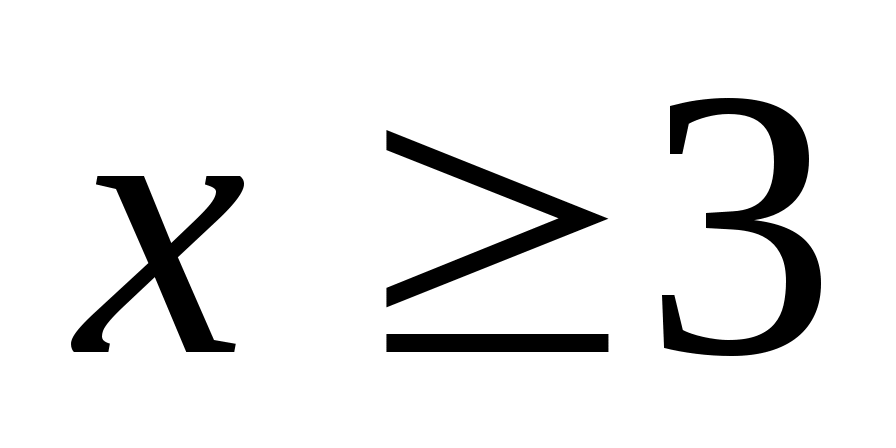 . Из уравнения
. Из уравнения 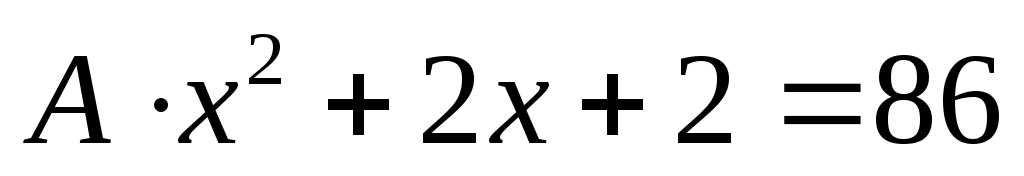 следует
следует 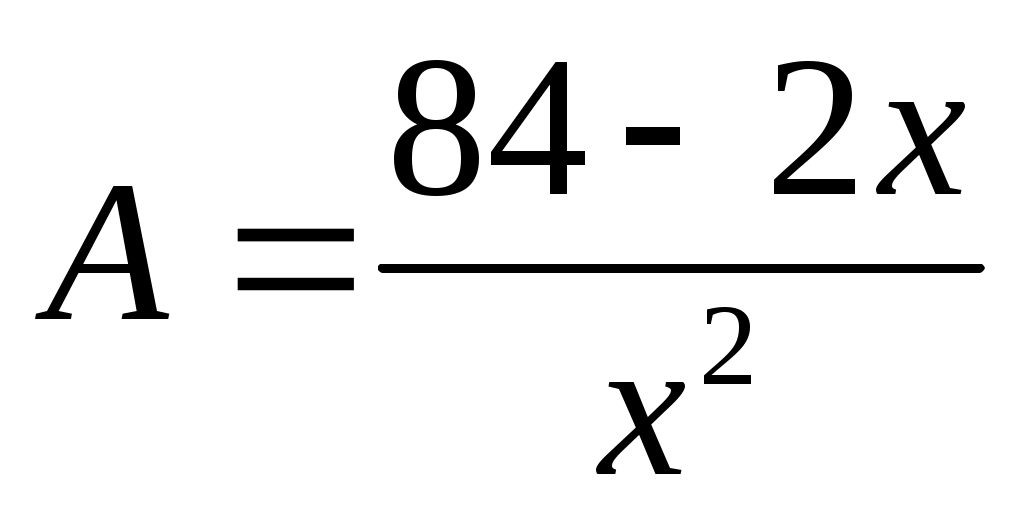 .
. -
очевидно, что чем меньше , тем больше
, тем больше  , поэтому значение
, поэтому значение  не превышает
не превышает 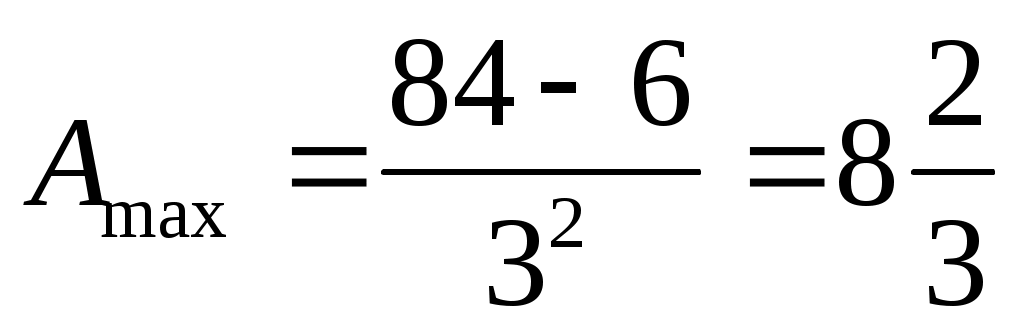
здесь мы подставили
-
остается перебрать все допустимые значения (от 0 до
(от 0 до 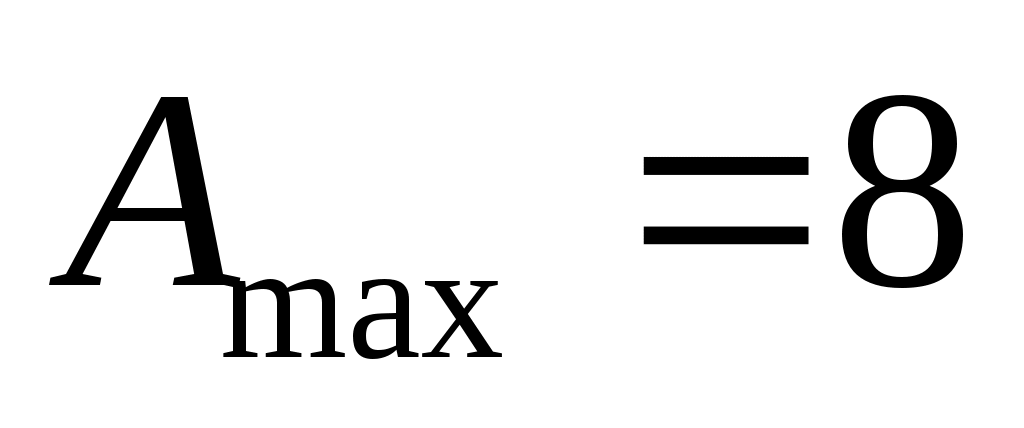 ), решая для каждого из них уравнение
), решая для каждого из них уравнение
относительно
-
получаем-
при :
: 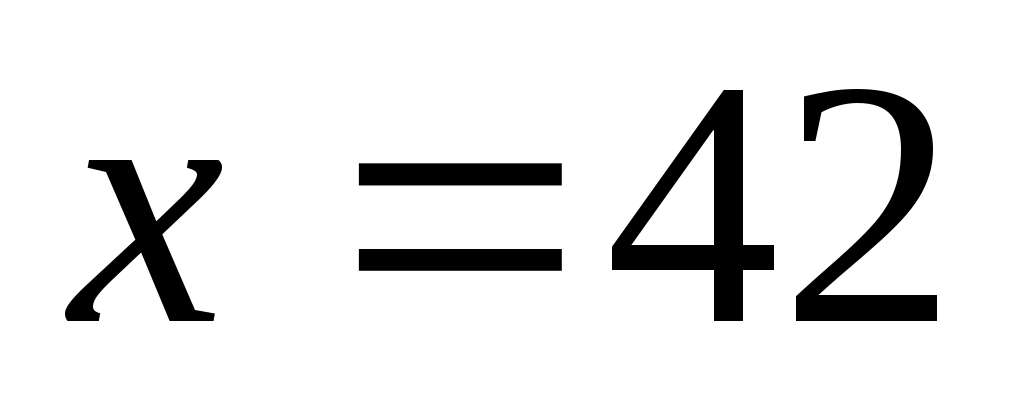
-
при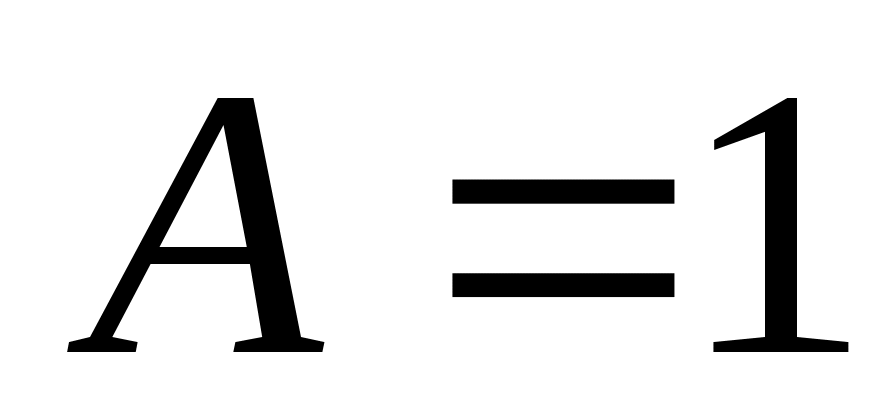 : решения – не целые числа
: решения – не целые числа -
при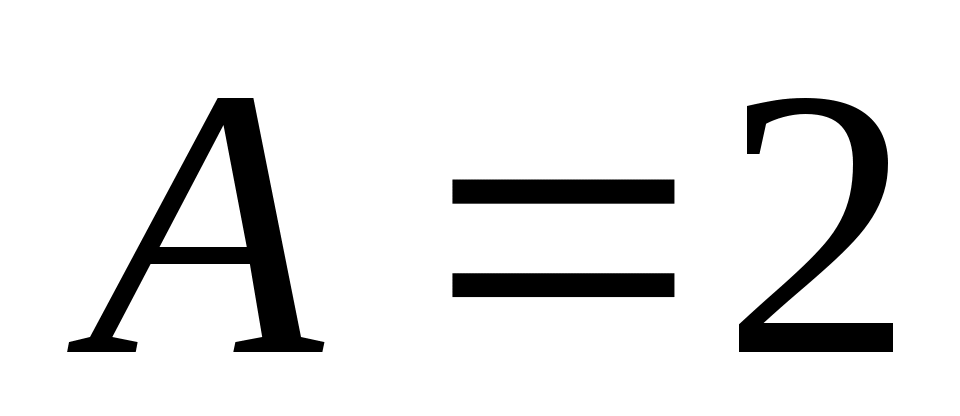 :
: 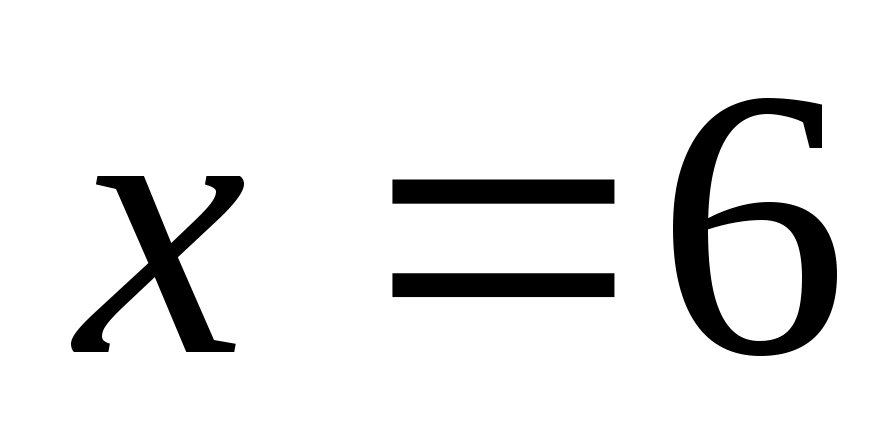 и
и 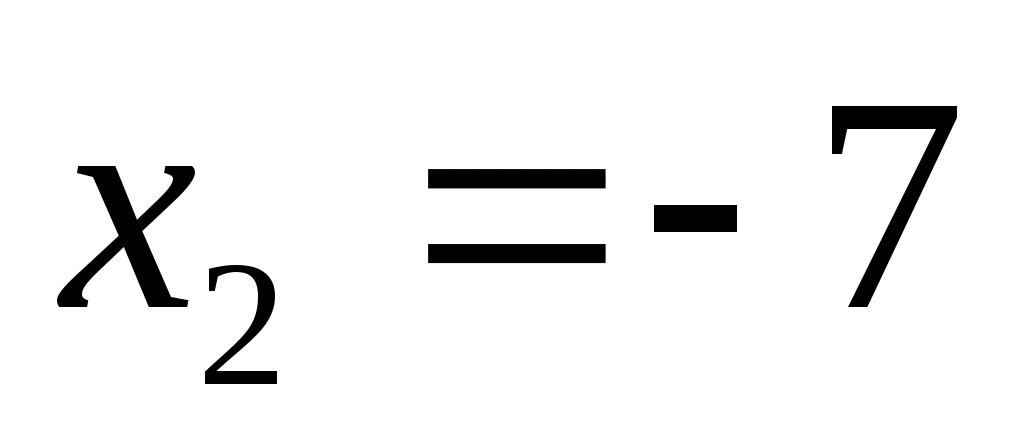 , второе решение не подходит
, второе решение не подходит -
при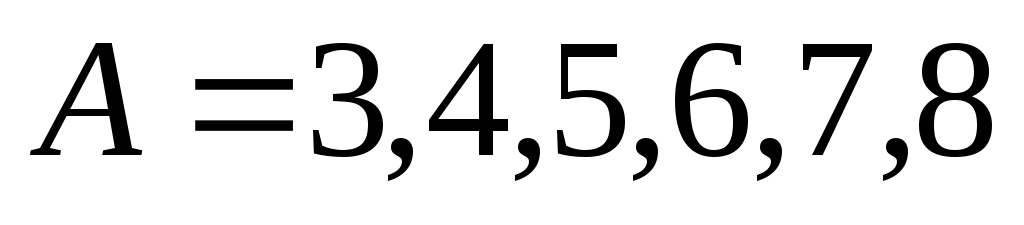 : решения – не целые числа
: решения – не целые числа
-
-
таким образом, верный ответ: 6, 42.
Решение (2 способ, М.В. Кузнецова и её ученики):
-
запись числа 86 в системе с основанием оканчивается на 22, т.е. в разряде единиц – 2, это значит, что остаток от деления 86 на
оканчивается на 22, т.е. в разряде единиц – 2, это значит, что остаток от деления 86 на  равен 2, то есть для некоторого целого
равен 2, то есть для некоторого целого имеем
имеем
-
таким образом, искомые основания – делители числа 84; остается выбрать из них те, которые соответствуют другим условиям задачи -
среди чисел, оканчивающихся на 22 в системе счисления с основанием ,минимальное – это само число
,минимальное – это само число 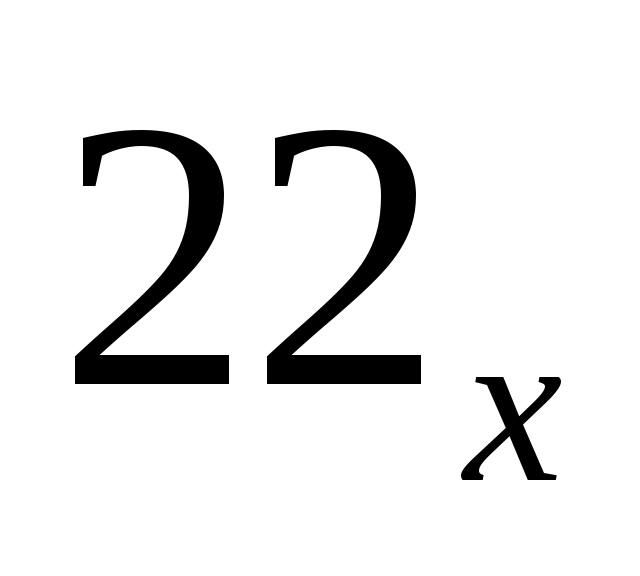 ; отсюда найдем максимальное основание:
; отсюда найдем максимальное основание:
так что первый ответ: 42.
-
остальные числа, окачивающиеся в этой системе на 22, имеют не менее 3-х знаков (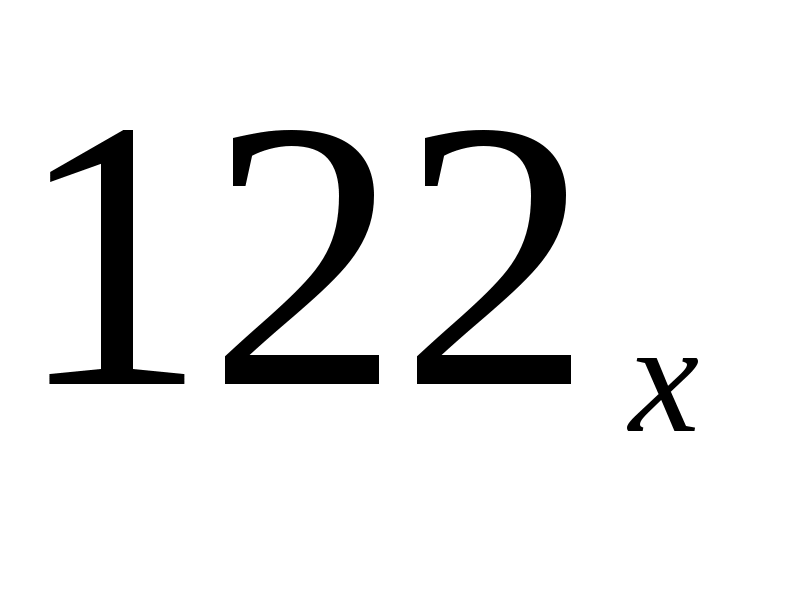 ,
,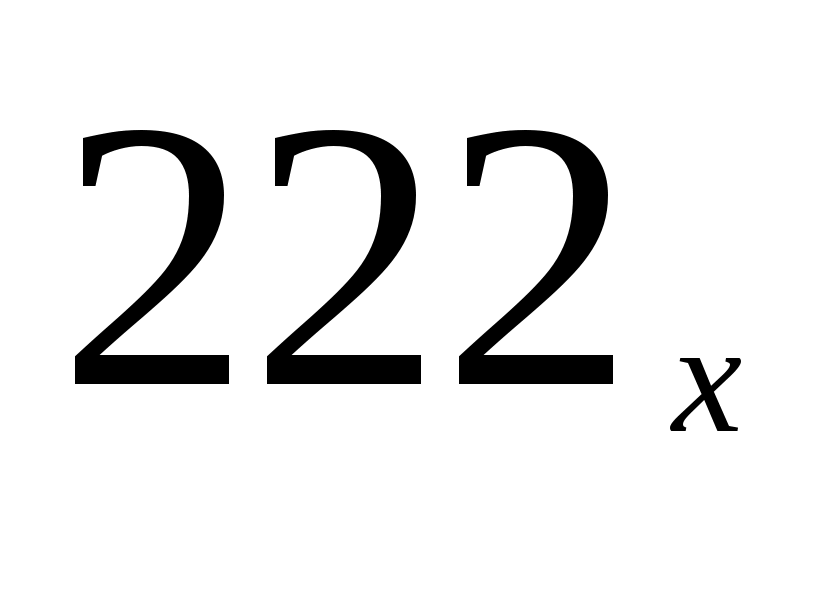 …), т.е. все они больше
…), т.е. все они больше 
-
поэтому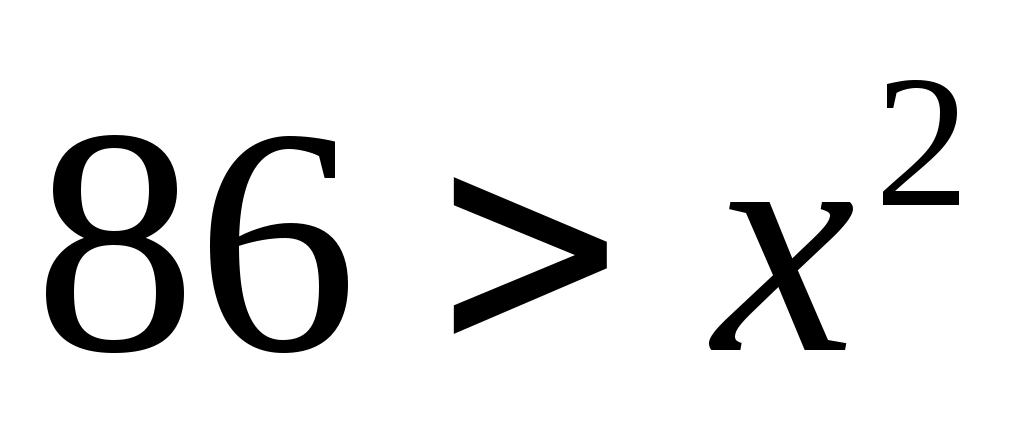 , следовательно,
, следовательно, 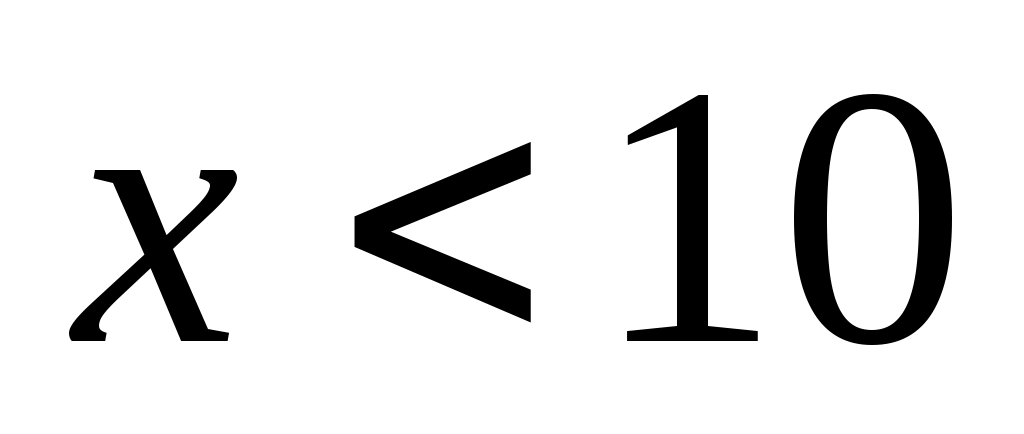
-
по условию в записи числа есть цифра 2, поэтому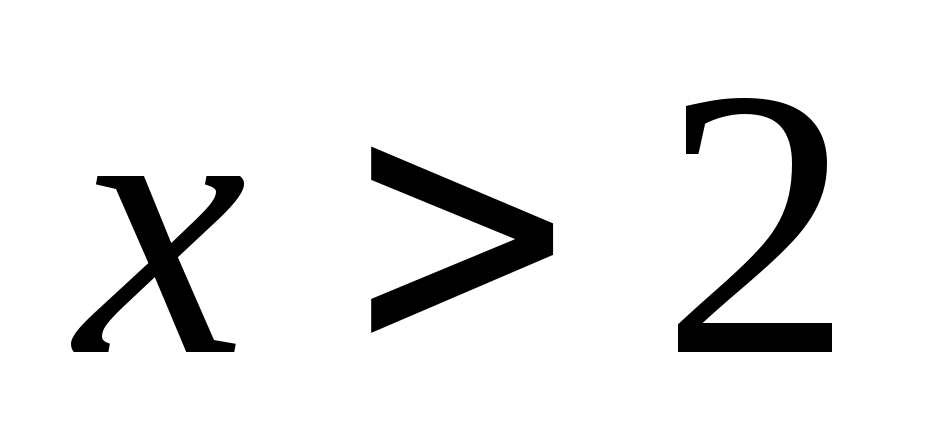
-
итак: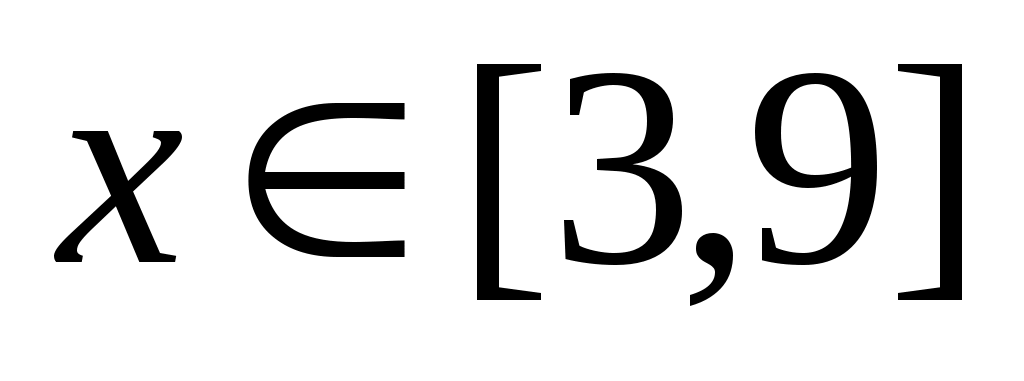 , и при этом
, и при этом  – делитель 84; возможные значения
– делитель 84; возможные значения 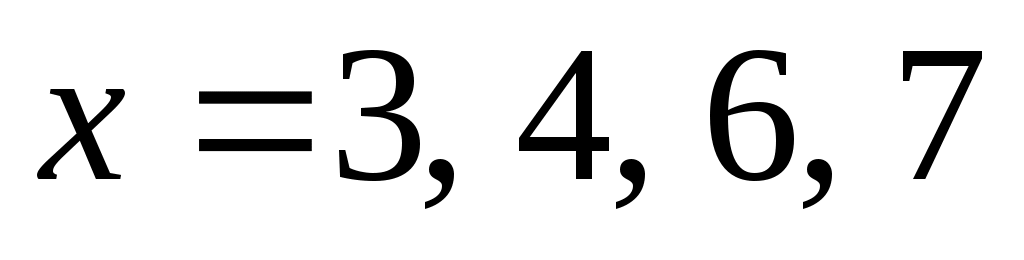 (на 5,8 и 9 число 84 не делится)
(на 5,8 и 9 число 84 не делится) -
переводя число 86 в системы счисления с основаниями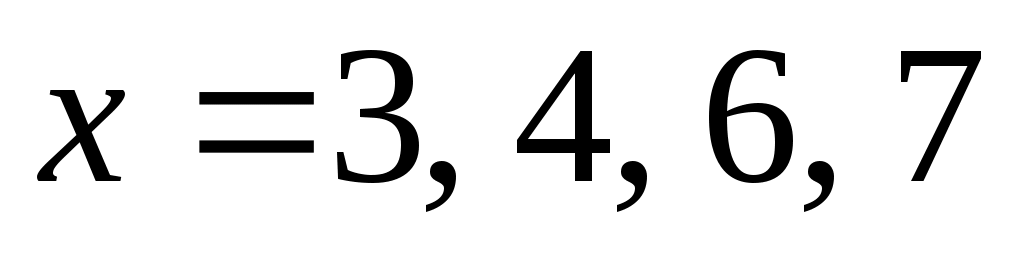 , находим, что только для основания 6 запись числа оканчивается на 22 (при делении на 3, 4 и 7 «вторые» остатки не равны 2):
, находим, что только для основания 6 запись числа оканчивается на 22 (при делении на 3, 4 и 7 «вторые» остатки не равны 2):
8
6
3
Дальше делить
нет смысла
8
6
4
8
6
6
8
6
7
8
4
2
8
3
8
4
2
1
4
8
4
1
4
6
8
4
1
2
7
2
2
7
9…
2
2
0
5…
2
1
2
2
2
7
1
1
1
2
5
-
таким образом, верный ответ: 6, 42.