ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 1052
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение (программа на Python, А.Н. Носкин):
-
можно решить задачу с помощью программы:
for i in range(3,100):# перебираем возможные основания
x = 86 # число по условию
x_N = ''
while x > 0:# перевод в N-ю систему
if x%i>9:break # пропускаем цифры в виде букв
else: x_N += str(x%i)
x //= i
x_N = x_N[::-1]# разворот числа
if x_N[-2:]== "22":
print(i, end=",")
-
ответ: 6, 42.
Решение (программа на Python, Б.С. Михлин):
-
полная программа:
for x in range(3, 86): # x - основание от 3 до 85
# (дальше перебирать нет смысла)
# справа число 22 переведено в 10-ую систему
if 86 % (x * x) == 2 * x + 2:
print( x, end = ',' )
-
Ответ: 6, 42.
Еще пример задания:
Р-03. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 94 начинается на 23.
Решение:
-
Из условия сразу видно, что искомое основание не меньше 4 (в записи есть цифра 3). -
Если запись числа 94 в некоторой системе счисления с основанием двузначна (94 = 23x), то справедливо равенство
двузначна (94 = 23x), то справедливо равенство 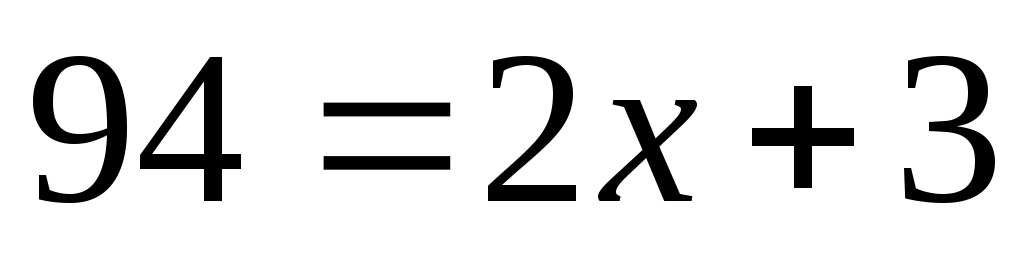 ; нас интересуют натуральные решения этого уравнения, такие что
; нас интересуют натуральные решения этого уравнения, такие что  , таких решений нет.
, таких решений нет. -
Предположим, что число четырехзначное. Минимальное допустимое четырехзначное число – 2300x, где . При минимальном основании (
. При минимальном основании ( ) оно равно
) оно равно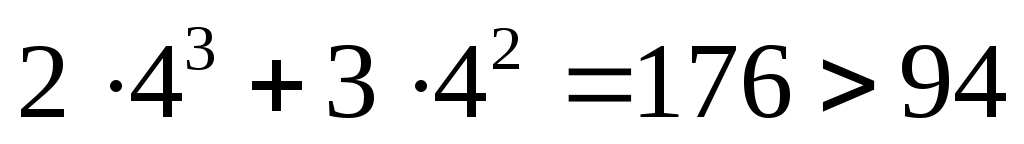 , поэтому запись нужного нам числа имеет не больше трех знаков.
, поэтому запись нужного нам числа имеет не больше трех знаков. -
На основании (2) и (3) делаем вывод, что число трехзначное, то есть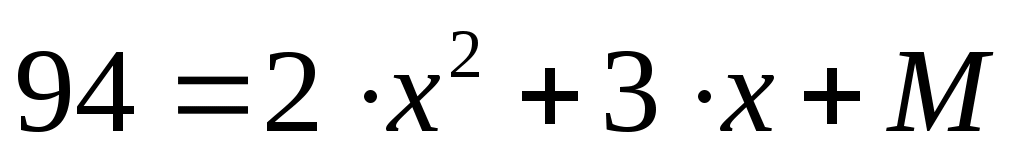 , где
, где 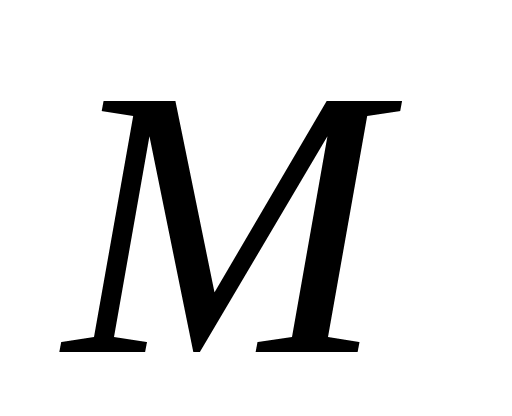 – целое неотрицательное число, такое что
– целое неотрицательное число, такое что 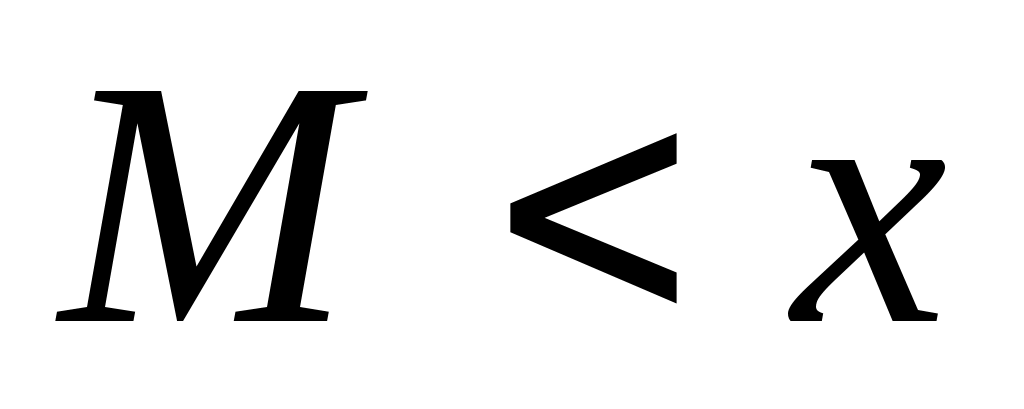 .
. -
Максимальное можно определить как решение уравнения
можно определить как решение уравнения 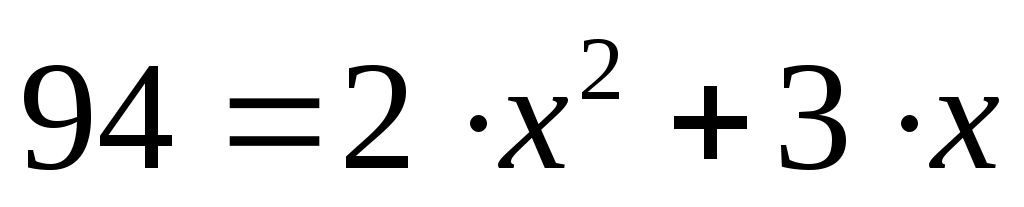 (при
(при 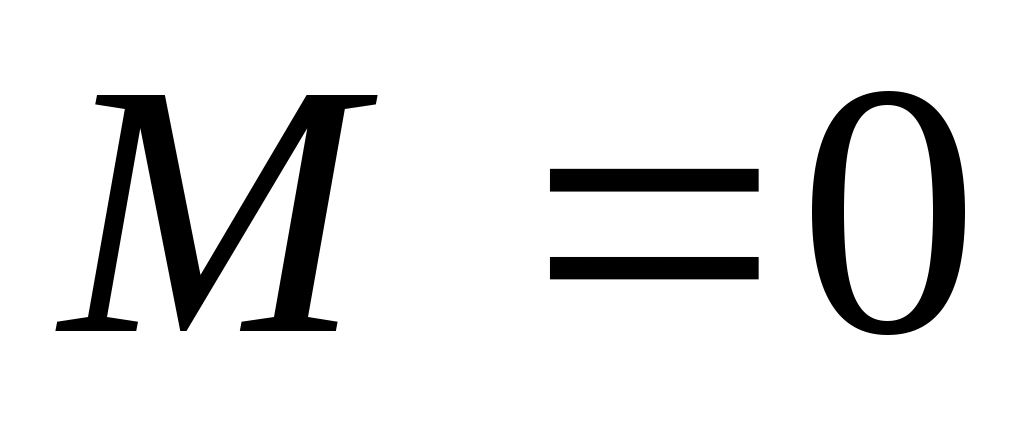 ); получаем одно из решений – 6,15; поэтому
); получаем одно из решений – 6,15; поэтому 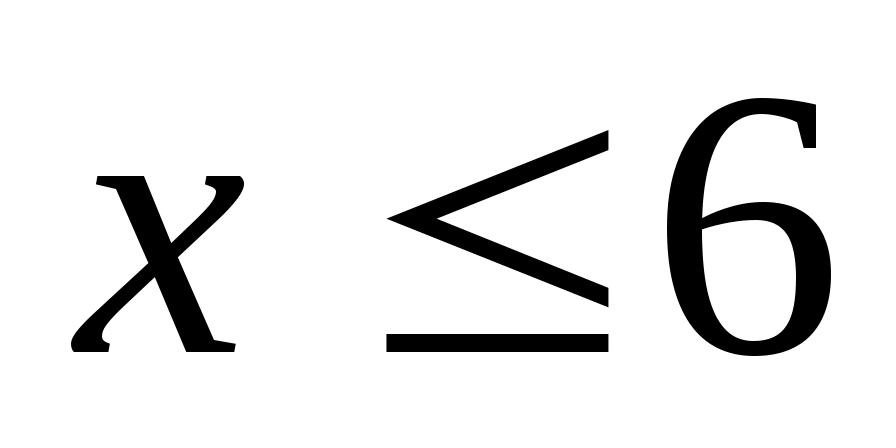
-
Если мы знаем , то
, то 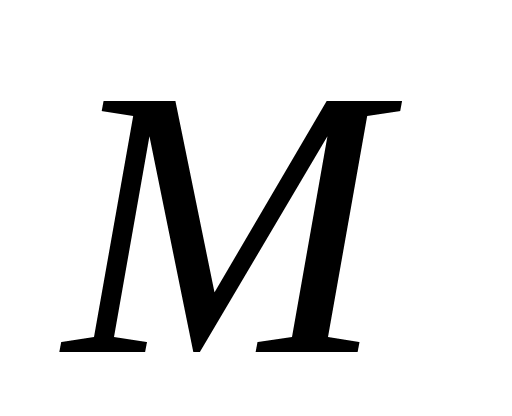 определится как
определится как 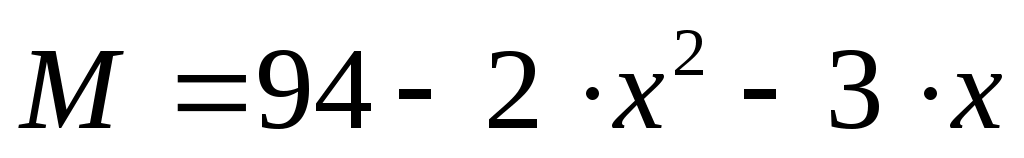 ; пробуем подставлять в эту формулу
; пробуем подставлять в эту формулу 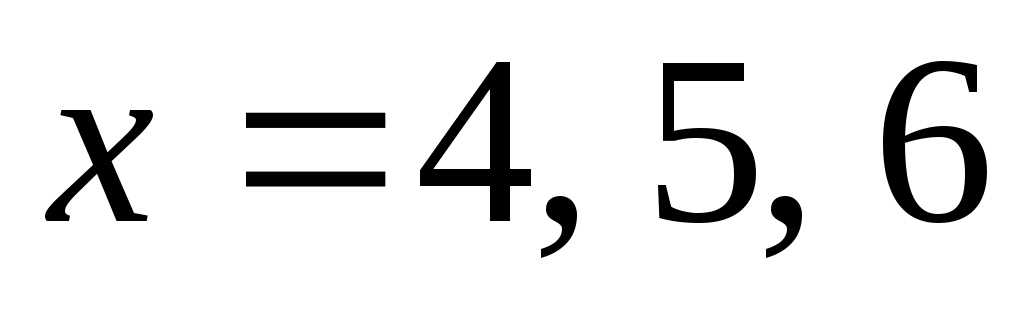 , пытаясь получить
, пытаясь получить 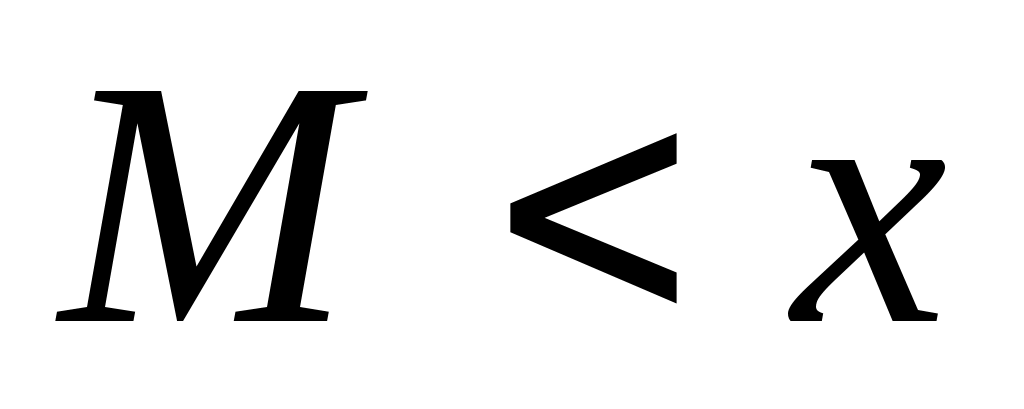
-
Минимальное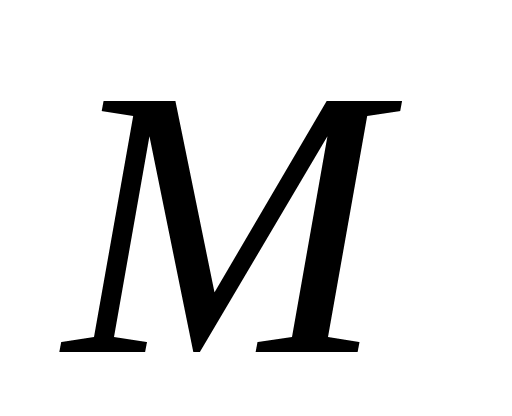 будет при
будет при  :
: 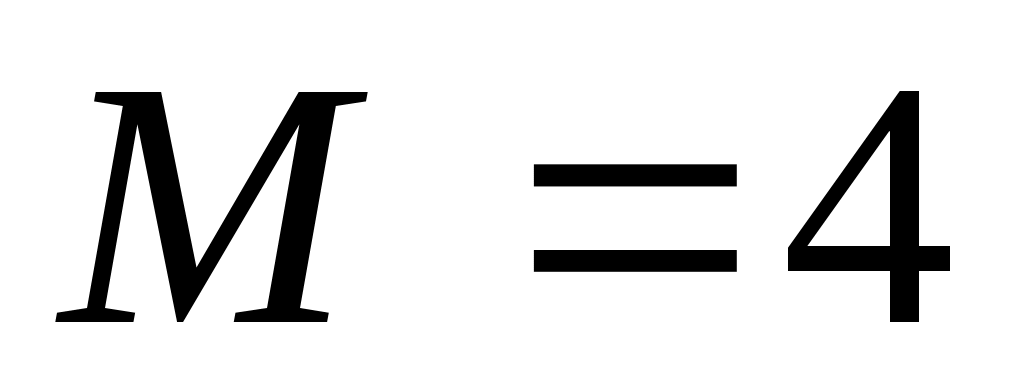 , а при
, а при 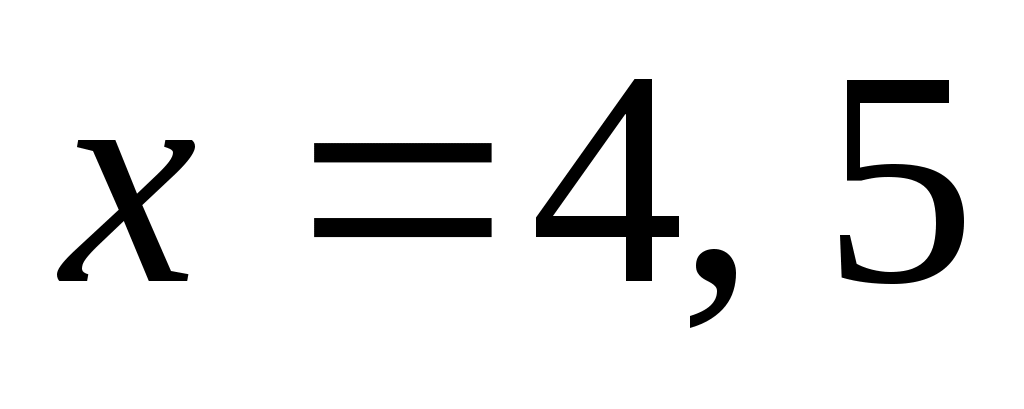 получается
получается 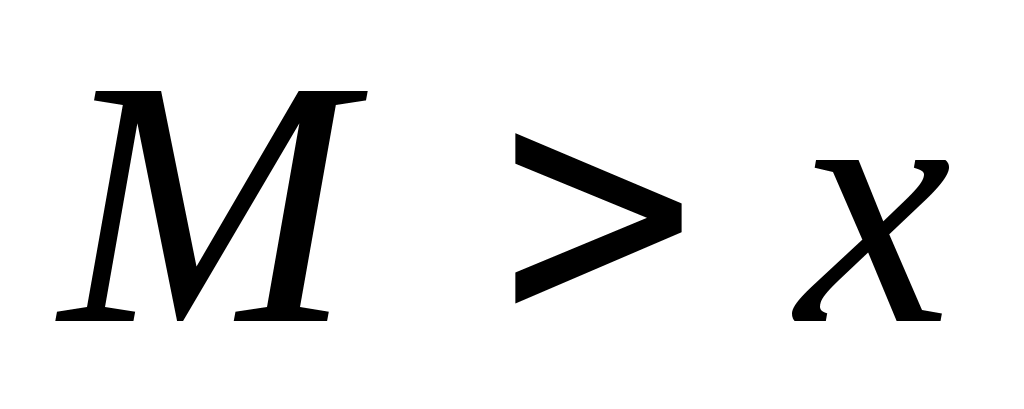
-
Таким образом, верный ответ: 6.
Решение (программа на Python, А.Н. Носкин):
-
можно решить задачу с помощью программы:
for i in range(4,100):# перебираем возможные основания
x = 94 # число по условию
x_N = ''
while x > 0:# перевод в N-ю систему
x_N += str(x%i)
x //= i
x_N = x_N[::-1]# разворот числа
if x_N[:2]== "23":
print(i, end=",")
-
ответ: 6.
Еще пример задания:
Р-2. Найти сумму восьмеричных чисел 178 +1708 +17008 +...+17000008, перевести в 16-ую систему счисления. Найдите в записи числа, равного этой сумме, третью цифру слева.
Решение:
-
Несложно выполнить прямое сложение восьмеричных чисел, там быстро обнаруживается закономерность:
178 + 1708 = 2078
178 + 1708 + 17008 = 21078
178 + 1708 + 17008 + 170008 = 211078
178 + 1708 + 17008 + 170008 + 1700008 = 2111078
178 + 1708 + 17008 + 170008 + 1700008 + 17000008 = 21111078
-
Переведем последнюю сумму через триады в двоичный код (заменяем каждую восьмеричную цифру на 3 двоичных):
100010010010010001112
-
Теперь разбиваем цепочку на тетрады (группы из 4-х двоичных цифр), начиная справа, и каждую тетраду представляем в виде шестнадцатеричной цифры
100010010010010001112
8 9 2 4 7
-
Таким образом, верный ответ (третья цифра слева): 2.
Решение (программа на Python, А.Н. Носкин):
-
решение задачи с помощью программы:
a = "17"
b = "1700000"
summa = 0
while a <= b:
summa += int(a,8) # перевод в 10ю систему
a += "0" # добавляем 0 к числу-строке
n16 = hex(summa)[2:] # перевод суммы в 16ю систему
print(n16[2])
-
Ответ: 2.
Решение (программа на Python, Б.С. Михлин):
-
полная программа:
x = 15 # 17 в 8-ой системе
s = x # s - сумма в 10-ой системе
for z in range( 1, 6 ): # z (zero) - количество нулей от 1 до 5
x *= 8 # добавление справа нуля к восьмеричному числу
# увеличивает его в 8 раз
s += x
print( hex( s )[4] ) # с учетом префикса '0x' третий символ
# (цифра) будет пятым с индексом 4
# print( hex( s ) ) # можно также найти третью цифру слева
-
Ответ: 2.
Еще пример задания:
Р-01. Чему равно наименьшее основание позиционной системы счисления
Решение:
-
Поскольку в левой и в правой частях есть цифра 5, оба основания больше 5, то есть перебор имеет смысл начинать с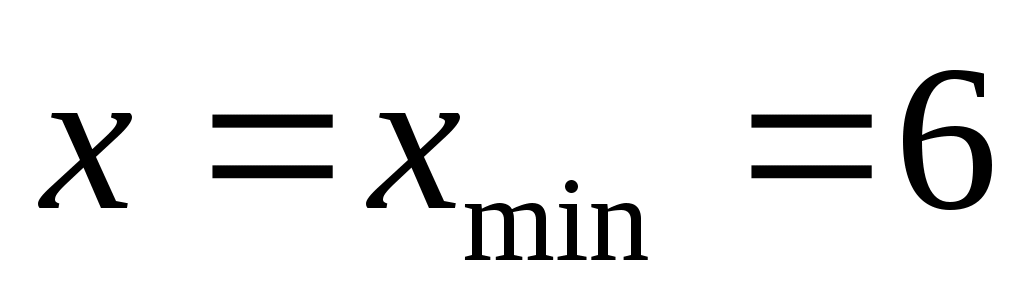 .
. -
Очевидно, что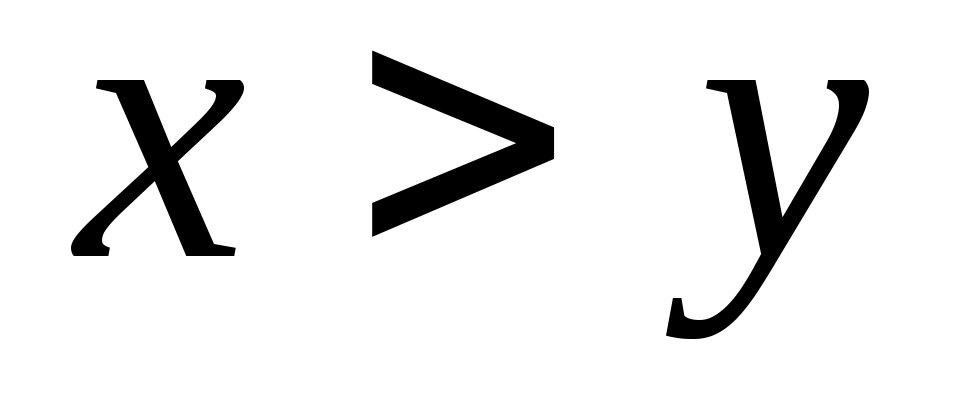 , однако это не очень нам поможет.
, однако это не очень нам поможет. -
Для каждого «подозреваемого» вычисляем значение
вычисляем значение 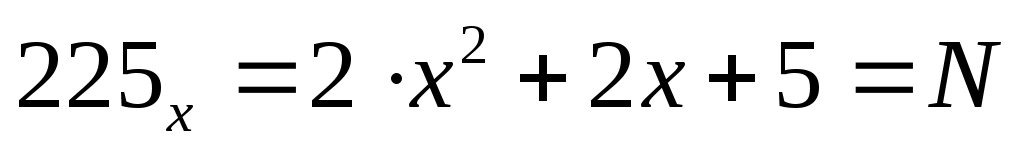 и решаем уравнение
и решаем уравнение 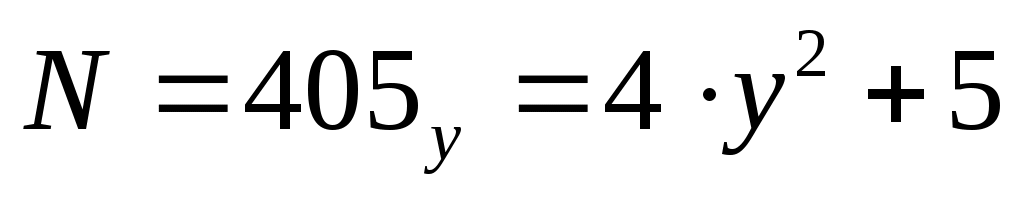 , причем нас интересуют только натуральные
, причем нас интересуют только натуральные 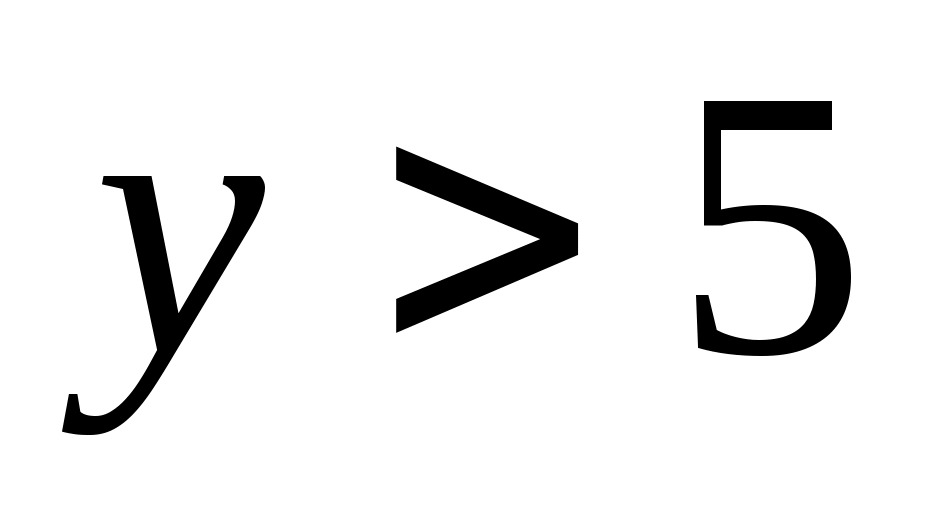 .
. -
Для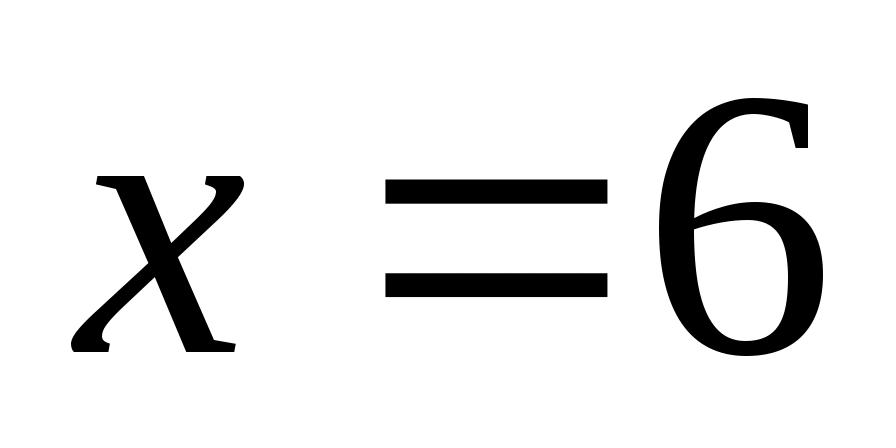 и
и 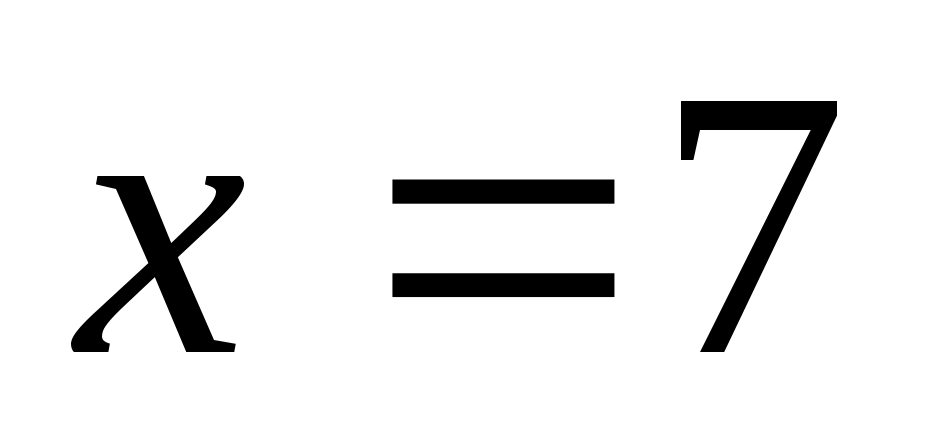 нужных решений нет, а для
нужных решений нет, а для 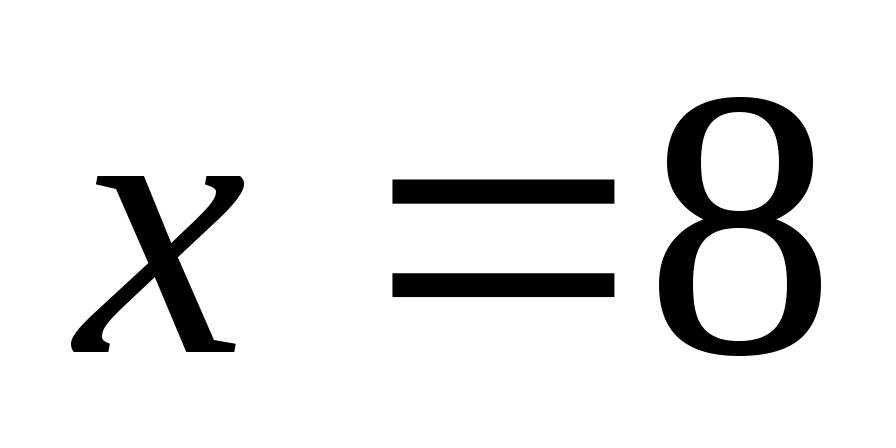 получаем
получаем
так что
-
Таким образом, верный ответ (минимальное значение ): 8.
): 8.
Решение (программа на Python, А.Н. Носкин):
-
можно решить задачу перебором с помощью программы (перебор начинаем с 6, так как цифра 5 есть в записи 225x, так и в записи 405y):
for x in range(6,20):# перебираем основания X
for y in range(6,20):# перебираем основания Y
if (2*x**2+2*x+5) == (4*y**2+0*y+5):
print(x)
break
-
ответ: 8.
Еще пример задания:
Р-00. Запись числа 3010 в системе счисления с основанием N оканчивается на 0 и содержит 4 цифры. Чему равно основание этой системы счисления N?
Решение (1 способ, подбор):
-
запись числа 30 в системе с основанием N длиннее, чем в десятичной (4 цифры против двух), поэтому основание N меньше 10 -
это дает шанс решить задачу методом подбора, переводя в разные системы, начиная с N = 2 до N = 9 -
переводим:
30 = 111102 = 10103 = …
-
дальше можно не переводить, поскольку запись 10103 удовлетворяет условию: заканчивается на 0 и содержит 4 цифры -
можно проверить, что при N ≥ 4 запись числа 30 содержит меньше 4 цифр, то есть не удовлетворяет условию -
Ответ: 3.
Решение (2 способ, неравенства):
-
запись числа 30 в системе с основанием N содержит ровно 4 цифры тогда и только тогда, когда старший разряд – третий, то есть
-
первая часть двойного неравенства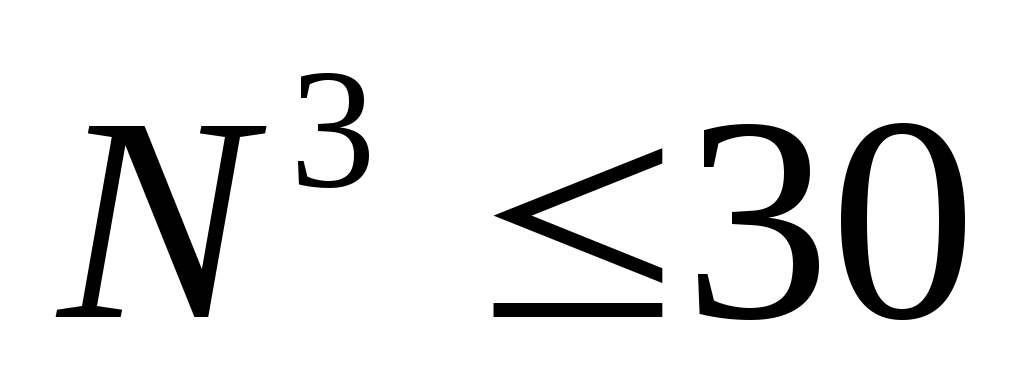 дает (в целых числах)
дает (в целых числах) 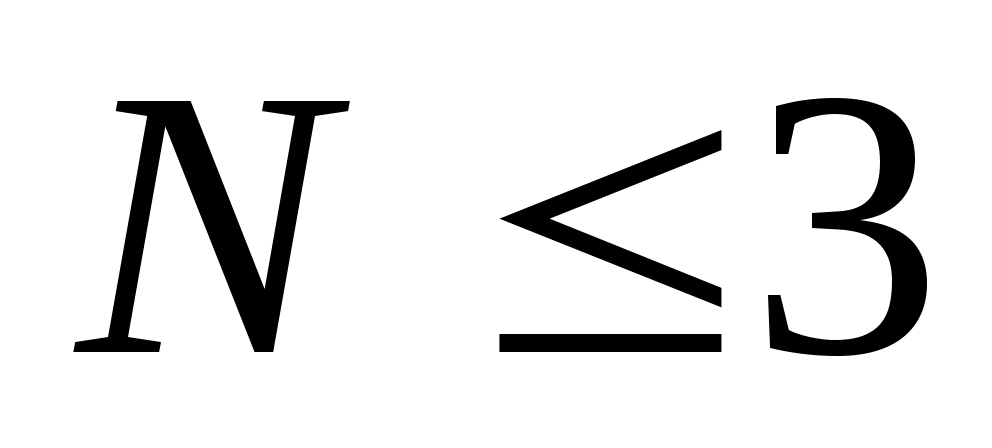
-
вторая часть неравенства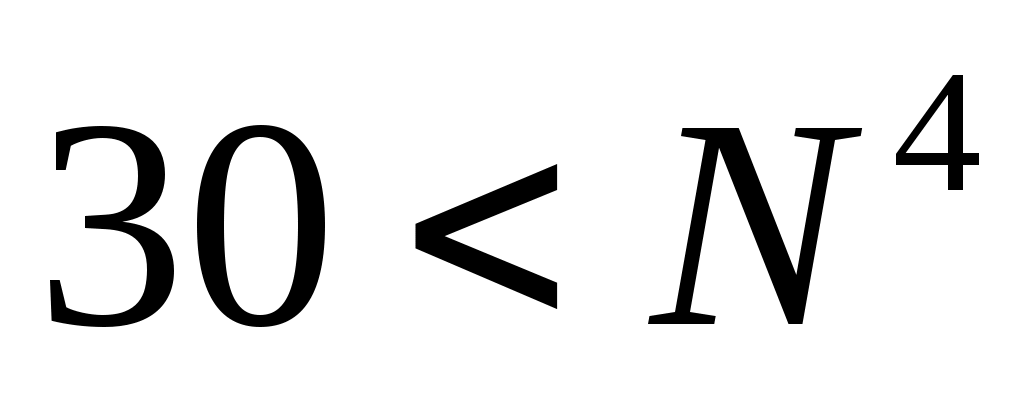 дает (в целых числах)
дает (в целых числах) 
-
объединяя результаты пп. 2 и 3 получаем, что N = 3 -
заметим, что условие «оканчивается на 0» – лишнее, ответ однозначно определяется по количеству цифр -
Ответ: 3.
Решение (программа на Python, А.Н. Носкин):
-
можно решить задачу перебором с помощью программы:
for i in range(2,36):# перебираем возможные основания
x = 30 # число по условию
x_N = ''
while x > 0:# перевод в N-ю систему
x_N += str(x%i)
x //= i
x_N = x_N[::-1]# разворот числа
if x_N[-1]== "0" and len(x_N) == 4:
print(i)
break
-
Ответ: 3.
Решение (программа на Python, Б.С. Михлин):
-
полная программа:
for N in range(2, 10): # проверять основание N >=10 нет смысла
# (будет два или один разряд)
# проверка на четырёхзначность (в этой задаче проверка
# окончания на ноль не обязательна)
if N**3 <= 30 < N**4 and 30 % N == 0:
print(N)
-
Ответ: 3.