Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 134
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
необходимости сокращения шага интегрирования вдвое является сохранение в памяти ЭВМ результатов промежуточных вычислений для исходного шага и дополнение их результатами расчетов, связанных с введением на отрезках интегрирования дополнительных точек, располагающихся в их середине.
Рассмотрим пример численного интегрирования. Зададим функцию
f x sinx2 0.2
Определим концы отрезка интегрирования
1; .
2
Требуется найти приближенное значение определенного интеграла
от функции
f x
тремя рассмотренными методами. Погрешность
результата не должна превышать
0.001.
 Для сравнения воспользуемся встроенной функцией приближенного вычисления определенного интеграла:
Для сравнения воспользуемся встроенной функцией приближенного вычисления определенного интеграла:
Результат вычисления: 0.4965223140806456.
Запишем правую часть формулы левыхпрямоугольников (3.5) как
функцию от числа отрезков n.Так как
x a ih a bai.
i n
Вычислим точность вычисления определенного интеграла по формуле (3.13) в зависимости от количества отрезков n.

Требуемая
точность была достигнута при n= 67. Приближенное
значение интеграла с заданной точностью прямоугольников равно 0.4975295296819863.
0.001
по формуле левых
Запишем правую часть формулы средних прямоугольников (3.7)
как функцию от числа отрезков n. Так как
x a ih a bai.
i n
Точность вычисления определенного интеграла в зависимости от числа отрезков n найдем по формуле (3.13).

При
n 6
приближенное значение интеграла по формуле средних
прямоугольников равно 0.4968543017618265 с точностью 9.985166509519083*10^-4 .
Запишем правую часть формулы правых прямоугольников (3.5)
как функцию от числа отрезков n.Так как
x a ih a bai.
i n
Определим точность вычисления интеграла по формуле (3.13):

При
n 69
приближенное значение интеграла по формуле правых
прямоугольников равно 0.4955340503706018 с точностью 9.982708115104377*10^-4.
Запишем правую часть формулы трапеций (3.6) как функцию
от числа отрезков n.Так как
x a ih a bai.
i n
Точность вычисления определим по формуле (3.13) в зависимости от числа отрезков n.

При
n 5
приближенное значение интеграла по формуле
трапеций равно 0.4955661821417044
с точностью 9.580511825193483*10^-4.
Запишем правую часть формулы парабол (3.9) как функцию
от числа отрезков n.Так как
x a ih a bai.
i n
Найдем точность вычисления по формуле (3.13).

При
n 2
приближенное значение интеграла по формуле


 парабол равно 0.4965270391248789 с точностью 4.725044233366837*10^-6.
парабол равно 0.4965270391248789 с точностью 4.725044233366837*10^-6.
b
Задача 1. Найти интеграл f(x)dxаналитически с помощью формулы Нью-
a
тона-Лейбница
Задача 2. Найти неопределенный интеграл с помощью программы wxMaxima.
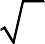
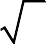










b
Задача 6. Вычислить интеграл f(x)dxметодом левых прямоугольников.
a
b
Задача 7. Вычислить интеграл f(x)dxметодом средних прямоугольников.
a
b
Задача 8. Вычислить интеграл f(x)dxметодом правых прямоугольников.
a
b
Задача 9. Вычислить интеграл f(x)dxметодом трапеций.
a
-
Численное интегрирование с помощью программы wxMaxima
Рассмотрим пример численного интегрирования. Зададим функцию
f x sinx2 0.2
Определим концы отрезка интегрирования
1; .
2
Требуется найти приближенное значение определенного интеграла
от функции
f x
тремя рассмотренными методами. Погрешность
результата не должна превышать
0.001.
 Для сравнения воспользуемся встроенной функцией приближенного вычисления определенного интеграла:
Для сравнения воспользуемся встроенной функцией приближенного вычисления определенного интеграла:Результат вычисления: 0.4965223140806456.
Формула левых прямоугольников.
Запишем правую часть формулы левыхпрямоугольников (3.5) как
функцию от числа отрезков n.Так как
x a ih a bai.
i n
Вычислим точность вычисления определенного интеграла по формуле (3.13) в зависимости от количества отрезков n.

Требуемая
точность была достигнута при n= 67. Приближенное
значение интеграла с заданной точностью прямоугольников равно 0.4975295296819863.
0.001
по формуле левых
Формула средних прямоугольников.
Запишем правую часть формулы средних прямоугольников (3.7)
как функцию от числа отрезков n. Так как
x a ih a bai.
i n
Точность вычисления определенного интеграла в зависимости от числа отрезков n найдем по формуле (3.13).

При
n 6
приближенное значение интеграла по формуле средних
прямоугольников равно 0.4968543017618265 с точностью 9.985166509519083*10^-4 .
Формула правых прямоугольников.
Запишем правую часть формулы правых прямоугольников (3.5)
как функцию от числа отрезков n.Так как
x a ih a bai.
i n
Определим точность вычисления интеграла по формуле (3.13):

При
n 69
приближенное значение интеграла по формуле правых
прямоугольников равно 0.4955340503706018 с точностью 9.982708115104377*10^-4.
Формула трапеций.
Запишем правую часть формулы трапеций (3.6) как функцию
от числа отрезков n.Так как
x a ih a bai.
i n
Точность вычисления определим по формуле (3.13) в зависимости от числа отрезков n.

При
n 5
приближенное значение интеграла по формуле
трапеций равно 0.4955661821417044
с точностью 9.580511825193483*10^-4.
Формула Симпсона.
Запишем правую часть формулы парабол (3.9) как функцию
от числа отрезков n.Так как
x a ih a bai.
i n
Найдем точность вычисления по формуле (3.13).

При
n 2
приближенное значение интеграла по формуле


 парабол равно 0.4965270391248789 с точностью 4.725044233366837*10^-6.
парабол равно 0.4965270391248789 с точностью 4.725044233366837*10^-6.ЗАДАНИЕ 2
b
Задача 1. Найти интеграл f(x)dxаналитически с помощью формулы Нью-
a
тона-Лейбница
Задача 2. Найти неопределенный интеграл с помощью программы wxMaxima.
| | f(x) | [a,b] | | f(x) | [a,b] |
| 1 | 1 tg2x 1 | [0.4; 0.8] | 21 | xarctg(2x) | [0,1; 0.3] |
| 2 | cos 3x (1 cos 3x)2 | [0.8; 1.6] | 22 | exsin 2x | [2; 2.4] |
| 3 | 1 x x3 4 | [0.18; 0.98] | 23 | ctg3x(cos 3x)2 | [1.2; 1.4] |
| 4 | sin x 1 sin x | [0.8; 1.6] | 24 | 3 x3 ln2 x | [1.2; 1.6] |
| 5 | arctg(1 x) | [0.1; 0.2] | 25 | arctg 2x1 | [0.6; 1.4] |
| 6 | x2 lg(x 2) | [0; 0.4] | 26 | (1 x)sin x | [1,4; 1.8] |
| 7 | x2arctg(x/ 3) | [0.8; 1.6] | 27 | cos x  1 cos x | [3.6;4] |
| 8 | e2x sin 3x | [0.4; 1.2] | 28 | 1 2x 2 ln 2x | [0.4; 1.4] |
| 9 | tg2x (sin 2x)2 | [0.8; 1.2] | 29 | (2x 3)cos x | [0.4; 0.6] |
| 10 | 4 x9 ln2 (4x) | [1.2; 1.4] | 30 | 1 x  2 x | [1.2; 1.6] |
| 11 | (2 x)sin x | [1; 1.5] | 31 | 2 x3 ln2 (2x) | [1.2; 1.4] |
| 12 | 5x xlg x | [0.2; 1] | 32 | x2 lg(2 x) | [1.4; 1.6] |
| 13 | (2x 3)sin x | [0.4; 1.2] | 33 | 3 x3 ln 3x | [0.4; 1] |
| 14 | 1 e x | [0.2; 0.6] | 34 | sin 2x  (2 3cos2 x)2 | [-1;0] |
| 15 | (2x 5) cos x | [0.4; 1.2] | 35 | 1 x4 x2 1 | [0.4; 0.6] |
| 16 | 1  1 x x2 | [0; 4] | 36 | x(2 lg x) | [1.2; 1.4] |
| 17 | arctg(1 x) | [0.7; 0.9] | 37 | arctg 3x1 | [0.4; 0.6] |
| 18 | 1 x  2 x | [0.4; 0.8] | 38 | 1 ex | [0.2; 0.6] |
| 19 | 1 ex | [1.4; 1.6] | 39 | 1  5 2x x2 | [-2.2; -1.2] |
| 20 | 1  sin4 x | [0.5;0.7] | 40 | (3x 5)cos x | [1, 1.4] |










| Задача 3. Вычислить определённый интеграл | с помощью | программы |
| wxMaxima. | | |
| Задача 4. Вычислить определённый интеграл | посредством | встроенной |
| функции приближенного вычисления quadpack. | | |
| Задача 5. Вычислить определённый интеграл | посредством | встроенной |
| функции приближенного вычисления romberg. | | |
b
Задача 6. Вычислить интеграл f(x)dxметодом левых прямоугольников.
a
b
Задача 7. Вычислить интеграл f(x)dxметодом средних прямоугольников.
a
b
Задача 8. Вычислить интеграл f(x)dxметодом правых прямоугольников.
a
b
Задача 9. Вычислить интеграл f(x)dxметодом трапеций.
a