Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 132
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример 5. Вычислить длину дуги кривой, заданной параметрически уравне-
ниями
x
t3
3 t, , где 0 t 3.
y t2 2,
Найдем производные
x t2 1, y 2t, тогда
dl
t t
 t2 12 2t2 dt
t2 12 2t2 dt t4 2t2 1dt
t4 2t2 1dt (t2 1)2 dt
(t2 1)2 dtВычислим длину дуги кривой:
3 3
t3
3 27
 L (t2 1)2 dt (t2 1)dt
L (t2 1)2 dt (t2 1)dt t 3 12

 0 0 3
0 0 30 3
Для решения подобных задач в wx Maxima следует выполнить следующие действия:
1. Построить кривую.
2. Вычислить производные функции.
3. В зависимости от способа задания кривой, составить и вычис- лить определенный интеграл с помощью программы Maxima и
вручную.
4. Записать ответ.
Пример 6. Вычислить длину дуги кривой
y lncos x, отсеченной прямы-
ми x 0 ,
x .
6
Построим график функции:
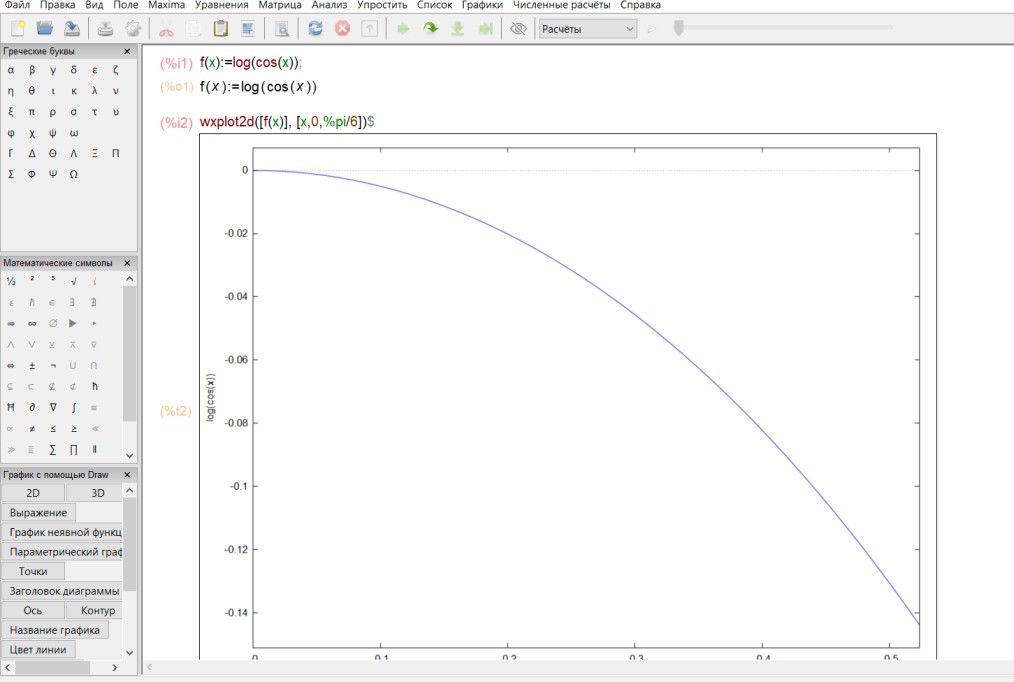
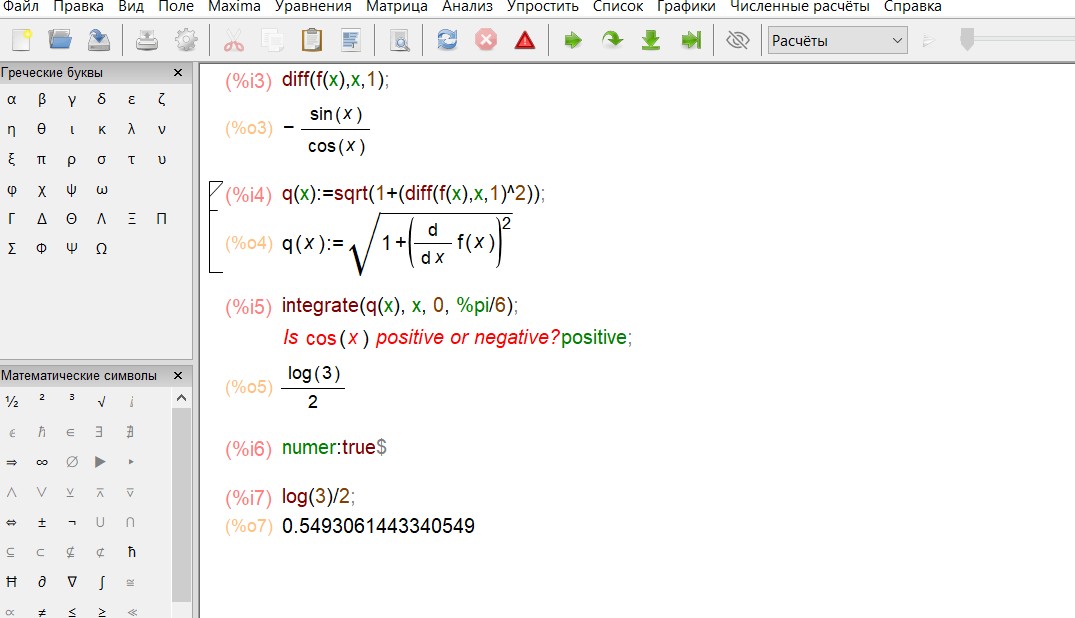
Найдем первую производную от данной функции и, затем, вычислим определенный интеграл. При вычислении интеграла появляется вопрос о
знаке функции cos x. Интегрирование мы проводим на отрезке
0, ,
здесь cos x> 0, значит, набираем positive.
6
Пример 7. Вычислить длину дуги кривой
x 2 cos3 t
при t 0, .
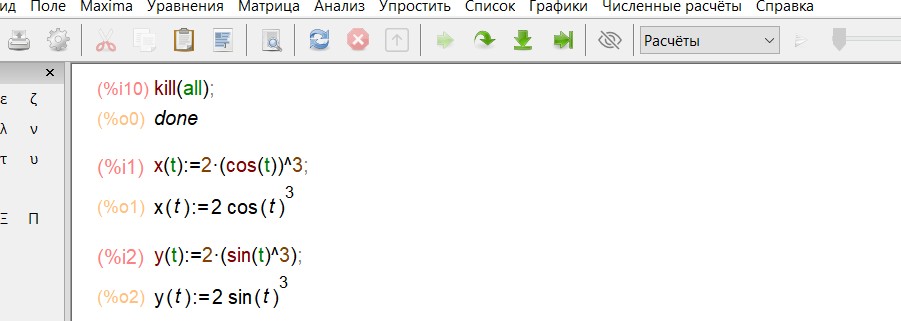
Зададим функцию и построим график функции:
y 2sin3 t
2
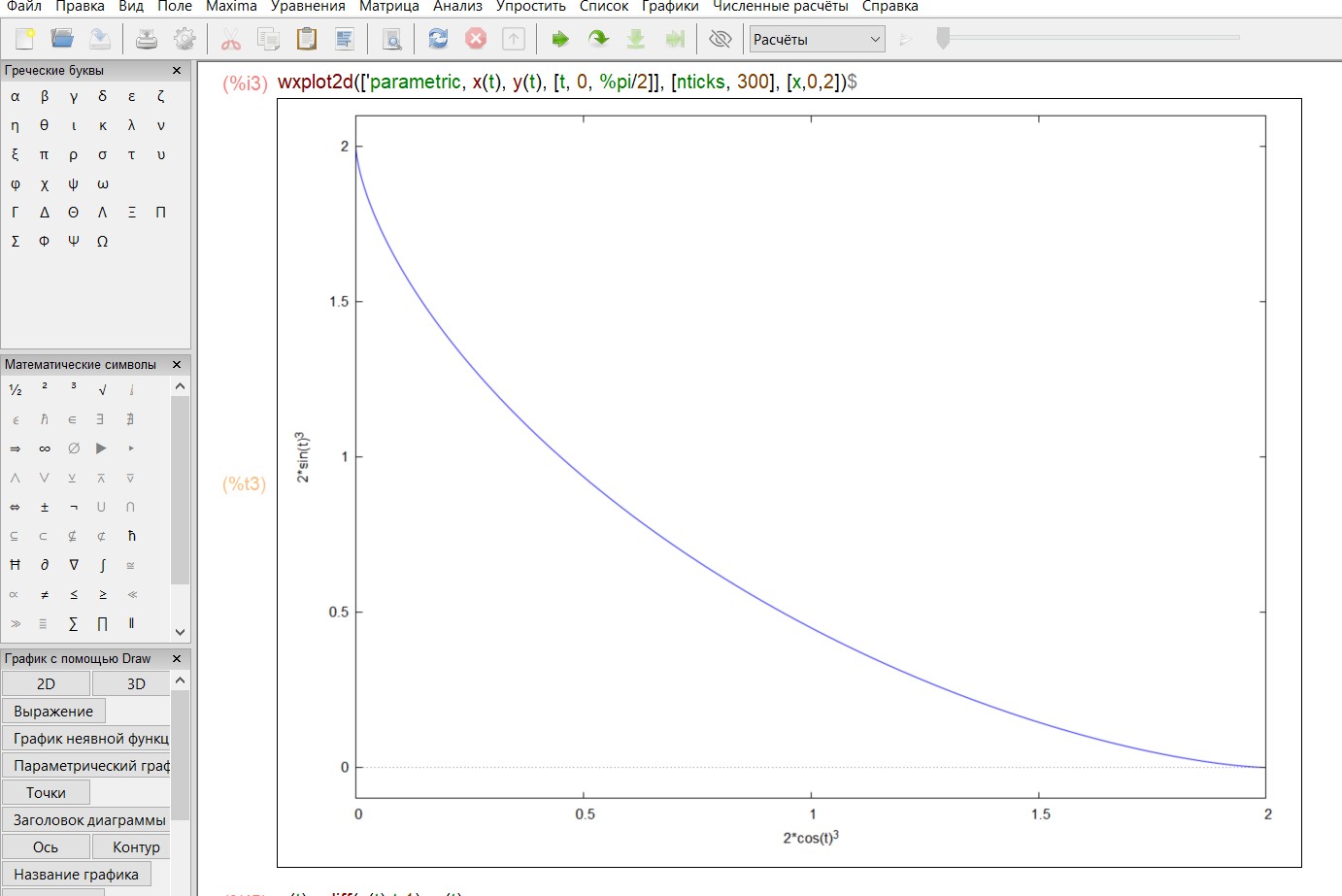
Найдем производные функций и вычислим определенный интеграл:
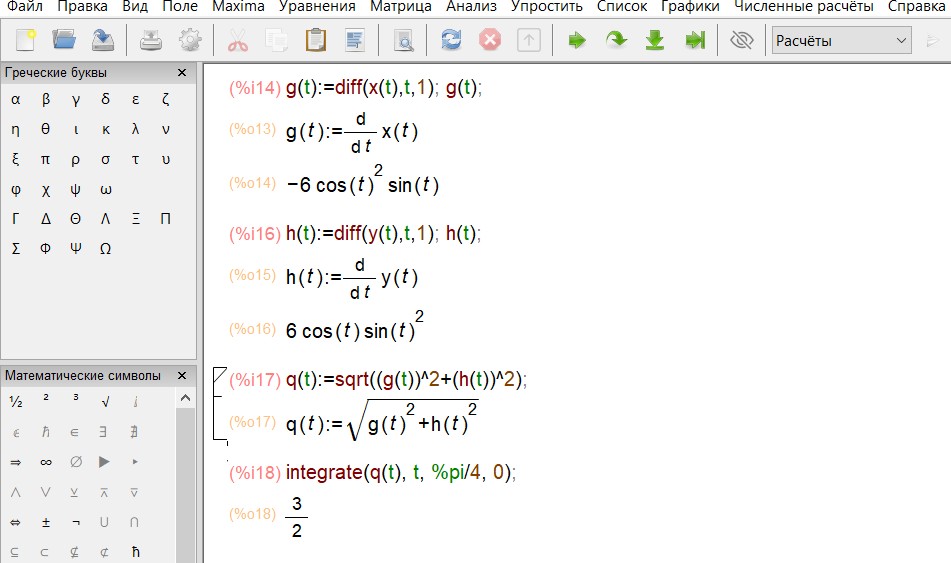
При вычислении интеграла появляется вопрос о знаке функции
cosx,sin x. Интегрирование мы проводим на отрезке
0, , здесь cos x
> 0, sin x>0, значит, positive.
4








 Задача 2. Вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат (аналитически и с
Задача 2. Вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат (аналитически и с
помощью программы wxMaxima).
| 1 | y ln x, 3 x 15. |
| 2 | x2 ln x y , 1 x 2. 4 2 |
| 3 | y 1 x2 arcsin x, 0 x 7 9. |
| 4 | y ln 5 , 3 x 8. 2x |
| 5 | y lncos x, 0 x 6. |
| 6 | y ex 6, ln 8 x ln 15. |
| 7 | y 2 arcsin x x x2 , 1 4 x 1. |
| 8 | y lnx2 1, 2 x 3. |
| 9 | y 1 x2 arccos x, 0 x 8 9. |
| 10 | y ln1 x2 , 0 x 1 4. |
| 11 | y 2 ch x, 0 x 1. |
| 12 | y 1 lncos x, 0 x 6. |
| 13 | y ex13, ln 15 x ln 24. |
| 14 | y arccos x x x2 , 0 x 1 4. |
| 15 | y 2 ex, ln 3 x ln 8. |
| 16 | y arcsin x 1 x2 , 0 x 15 16. |
| 17 | y 1 lnsin x, 3 x 2. |
| 18 | y 1 ln x2 1, 3 x 4. |
| 19 | y x x2 arccos x 5, 1 9 x 1. |
| 20 | y arccos x 1 x2 1, 0 x 9 16. |
| 21 | y lnsin x, 3 x 2. |
| 22 | y ln 7 ln x, 3 x 8. |
| 23 | y ch x 3, 0 x 1. |
| 24 | y 1 arcsin x 1 x2 , 0 x 3 4. |
| 25 | y lncos x 2, 0 x 6. |
| 26 | y ex 26, ln 8 x ln 24. |
| 27 | ex e x y 3, 0 x 2. 2 |
| 28 | y arccos x x x2 4, 0 x 1 2. |
| 29 | ex ex 3 y , 0 x 2. 4 |
| 30 | y ex e, ln 3 x ln 15. |
| 31 | 1 ex ex y , 0 x 3. 2 |
| 32 | x2 y , 0 x 1. 2 |
| 33 | y ln(1 x2 ), 0 x 0,5. |
| 34 | y ln(2cos x), 0 x . 3 |
| 35 | x x y e2 e 2 , 0 x 2. |
| 36 | y ln(2x 1), 5 x 29 . 2 5 |