Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 127
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример 3.
Вычислить площадь фигуры, ограниченной следующими линиями
y 4 , y = 0, ???? = 4, ???? = 0, ???? = 4.
x
Зададим функции
y 4 , y = 0, ???? = 4,
x
Вертикальные прямые ???? = 4 ???? = 0 в Maxima можно построить только, представив их уравнения в параметрическом виде:
x 4
y t
и x 0 .
y t
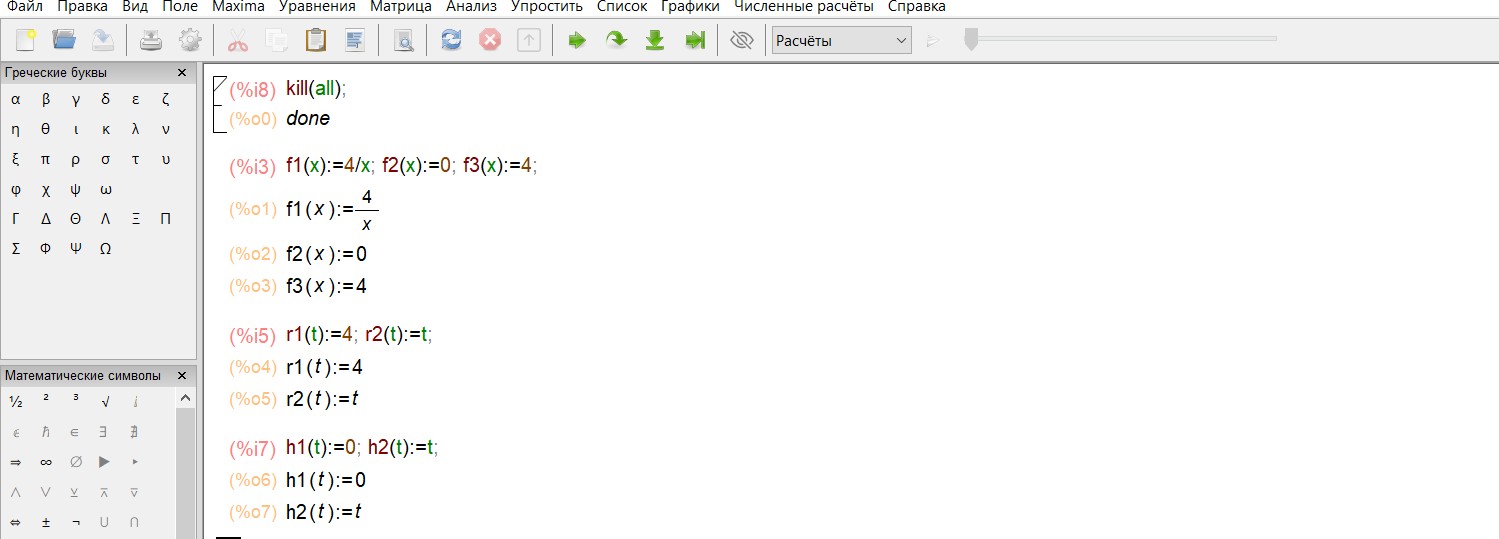
Теперь построим графики всех этих функций:
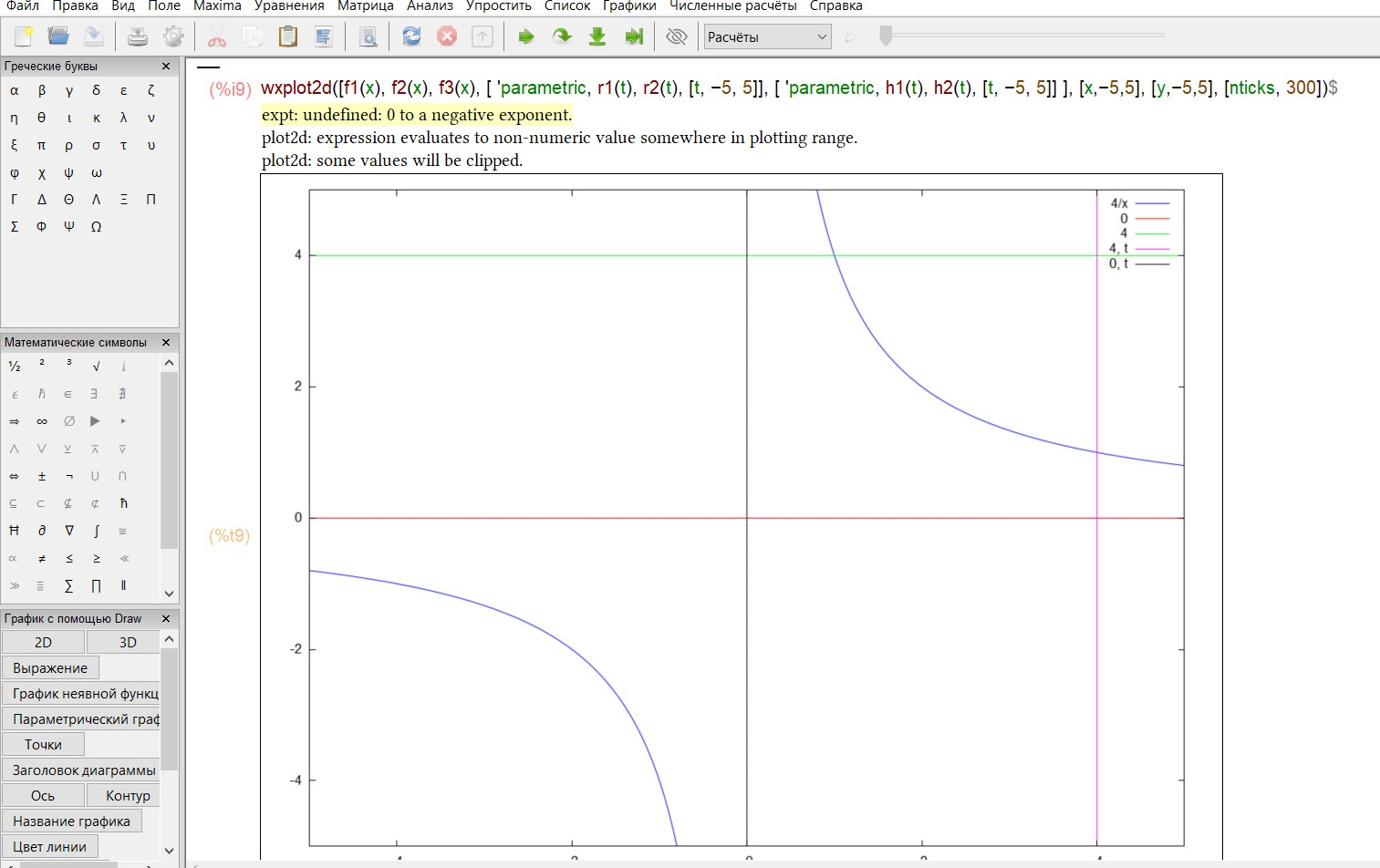
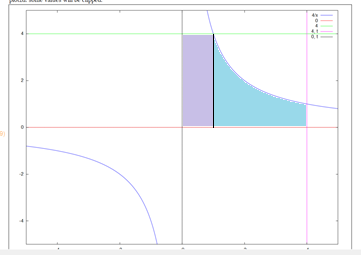 Чтобы вычислитьплощадь интересующей нас фигуры, необходимо поделить область на две части: от прямой х=1.
Чтобы вычислитьплощадь интересующей нас фигуры, необходимо поделить область на две части: от прямой х=1.Первая фигура является прямоугольником, ее площадь равна S1 4 1 4 . Площадь второй фигуры вычисляем с помощью определенного интеграла:

Площадь искомой фигуры равна
4 4 ln 4 .
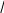









 ЗАДАНИЕ 1
ЗАДАНИЕ 1

 Задача 1. Вычислить площадь фигуры, ограниченной графиками функций (аналитически и с помощью программы wxMaxima). Выполнить построение.
Задача 1. Вычислить площадь фигуры, ограниченной графиками функций (аналитически и с помощью программы wxMaxima). Выполнить построение.| 1 | y x 23 , y 4x 8. | 2 | y x 9 x2 , y 0, 0 x 3. |
| 3 | y 4 x2 , y x2 2x. | 4 | y sin xcos2 x, y 0, 0 x 2. |
| 5 | y 4 x2 , y 0, x 0, x 1. | 6 | y x2 4 x2 , y 0, 0 x 2. |
| 7 | y cos xsin2 x, y 0, 0 x 2. | 8 | y ex1, y 0, x ln 2. |
| 9 | y 1 , y 0, x1 ln x x 1, x e3 . | 10 | y arccos x, y 0, x 0. |
| 11 | y x12 , y2 x1. | 12 | y 2x x2 3, y x2 4x 3. |
| 13 | y x 36 x2 , y 0, 0 x 6. | 14 | x arccos y, x 0, y 0. |
| 15 | y arctg x, y 0, x 3. | 16 | y x2 8 x2 , y 0, 0 x 2 2 . |
| 17 | x ey1, x 0, y ln 2. | 18 | y x 4 x2 , y 0, 0 x 2. |
| 19 | y x , y 0, 1 x x 1. | 20 | y 1 , y 0, 1 cos x x 2, x 2. |
| 21 | x y 23 , x 4 y 8. | 22 | y cos5 xsin 2x, y 0, 0 x 2. |
| 23 | y x , y 0, x2 12 x 1. | 24 | x 4 y2 , x y2 2 y. |
| 25 | y x , y 0, x2 12 x 1. | 26 | e1 x y , y 0, x2 x 2, x 1. |
| 27 | y x2 16 x2 , y 0, 0 x 4. | 28 | x 4 y2 , x 0, y 0, y 1. |
| 29 | y x12 , y2 x1. | 30 | y x2 cos x, y 0, 0 x 2. |
| 31 | x 4 y12 , x y2 4 y 3. | 32 | y x, x 16, y 1 . x |
| 33 | y arcsin x, y 0, x . 2 | 34 | x 8 y2, x 2 y. |
| 35 | y ex, x 1, y ex. | 36 | y sin x, y cos x, x 0, (x 0). |
| 37 | y 17 x2 , x 0, y 16 . x2 | 38 | y 2x x2 16, y 4x 8. |
| 39 | x2 1 y , y . 2 1 x2 | 40 | y 3 x, x 9, 2 y 3 . 2x |














Длина дуги
Длина дуги кривой y
f(x) ,
-
a, b вычисляется по формуле:
b
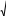 L
L a
1 fx2 dx.
Если уравнение кривой задано в параметрическом виде
x xt,
y yt,
то для вычисления длины этой кривой применяют формулу:
t2
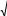 L
L t1
xt2 уt2 dt
Пример 4. Вычислить длину дуги кривой
y lnsin x
от x
до x
.
Из уравнения линии Тогда
y lnsin x
находим
y cos xи
 sin x
sin x1 3 2 2
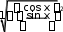 dl dx
dl dx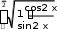

cos x
2dx
2
L dx ln tg
3 3
x
 1 ln 3
1 ln 32
3