ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 124
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, то верно, и заключение  . Это классическое правило вывода постоянно используется в математике, при переходе от одних высказываний к другим, с помощью доказываемых теорем, которые, как правило, имеют форму импликаций.
. Это классическое правило вывода постоянно используется в математике, при переходе от одних высказываний к другим, с помощью доказываемых теорем, которые, как правило, имеют форму импликаций.
В случае импликации несоответствие между обычным пониманием истинности сложного высказывания и идеализированной точкой зрения алгебры высказываний еще заметнее, чем для других логических операций. Здесь истинность импликации в некоторой ситуации означает лишь, что если в этой ситуации истинна посылка, то истинно и заключение.
Эквиваленция (эквивалентность, логическая эквивалентность). Эквиваленцией двух высказываний и
и  называется новое высказывание, которое истинно, когда оба высказывания
называется новое высказывание, которое истинно, когда оба высказывания  и
и  либо одновременно истинны, либо одновременно ложны, и ложно во всех остальных случаях. Обозначается
либо одновременно истинны, либо одновременно ложны, и ложно во всех остальных случаях. Обозначается  , читается "для того, чтобы
, читается "для того, чтобы  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  " или "
" или " тогда и только тогда, когда
тогда и только тогда, когда  ". Эквивалентность играет значительную роль в математических доказательствах. Известно, что большое число теорем формулируется в форме необходимых и достаточных условий. Это так называемые теоремы существования. Логические значения операции эквиваленции описываются в табл. 1.17.
". Эквивалентность играет значительную роль в математических доказательствах. Известно, что большое число теорем формулируется в форме необходимых и достаточных условий. Это так называемые теоремы существования. Логические значения операции эквиваленции описываются в табл. 1.17.
Таблица 1.17
С помощью логических операций над высказываниями можно строить различные новые, более сложные высказывания. Всякое сложное высказывание, которое может быть получено из элементарных высказываний с помощью логических связок, называется формулой алгебры логики. Формулы алгебры логики обозначаются большими буквами латинского алфавита ,
, 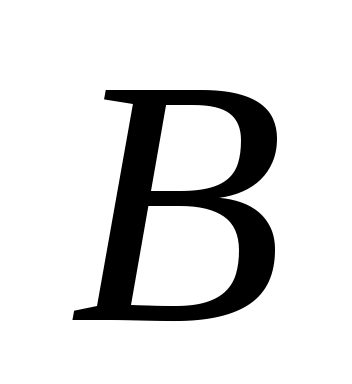 ,
, 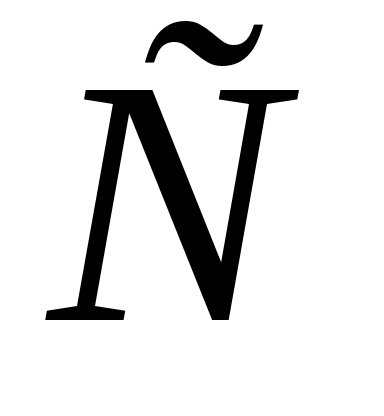 , … Две формулы алгебры логики
, … Две формулы алгебры логики  и
и 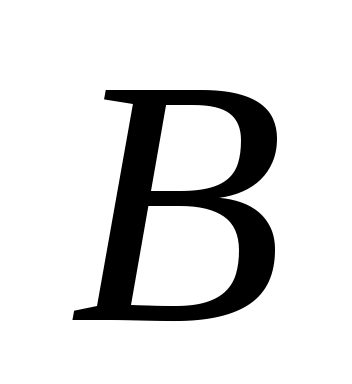 называются равносильными, если они принимают одинаковые логические значения при любом наборе значений, входящих в формулы элементарных высказываний. Равносильность обозначается знаком " ≡ ".
называются равносильными, если они принимают одинаковые логические значения при любом наборе значений, входящих в формулы элементарных высказываний. Равносильность обозначается знаком " ≡ ".
Для любых формул ,
, 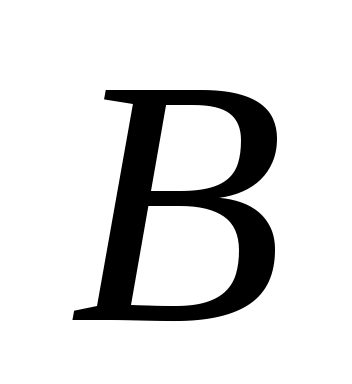 ,
, 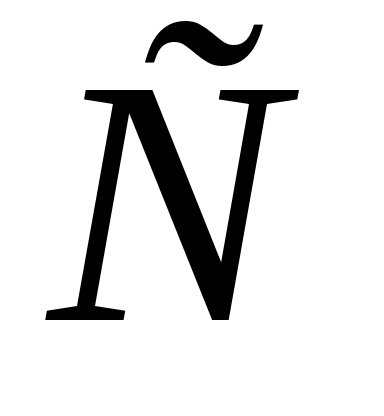 справедливы следующие равносильности.
справедливы следующие равносильности.
 — истина;
— истина;
Все эти соотношения легко проверяются по таблицам истинности.
Именно из равносильностей этой группы формул следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.
Формула называется тождественно истинной или тавтологией, если она принимает значение 1 при всех значениях входящих в нее переменных. Формула
называется тождественно истинной или тавтологией, если она принимает значение 1 при всех значениях входящих в нее переменных. Формула  называется
называется
тождественно ложной или противоречивой, если она равна 0 при всех значениях входящих в нее переменных.
Формула алгебры логики является функцией входящих в нее элементарных высказываний, ее аргументы принимают два значения 0 и 1, при этом значение формулы может быть равно 0 или 1.
Функцией алгебры логики переменных (или функцией Буля) называется функция
переменных (или функцией Буля) называется функция  логических переменных, то есть функцией алгебры логики
логических переменных, то есть функцией алгебры логики 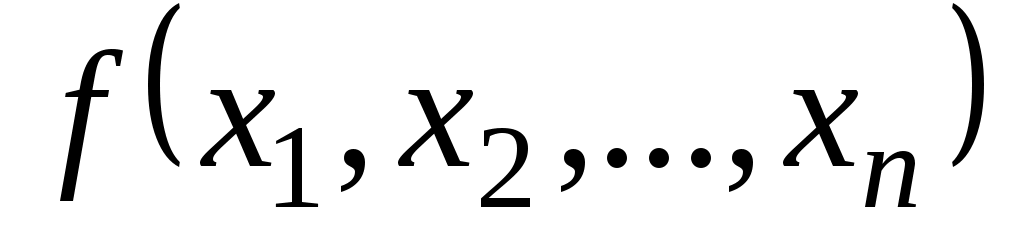 от
от  переменных
переменных 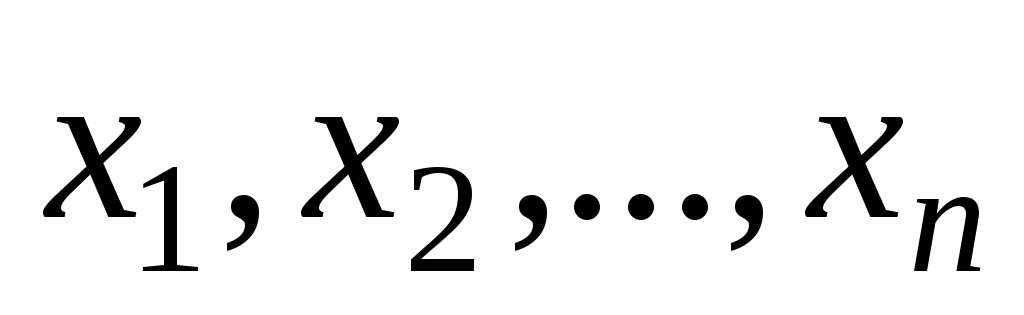 называется функция, принимающая значения 0, 1, аргументы которой также принимают значения 0, 1.
называется функция, принимающая значения 0, 1, аргументы которой также принимают значения 0, 1.
Функция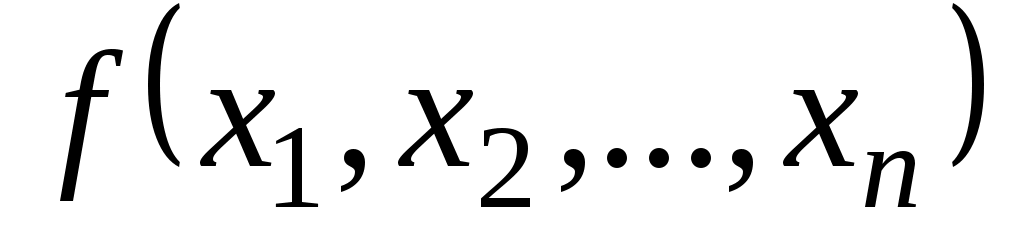 задается своей истинностной таблицей 1.18.
задается своей истинностной таблицей 1.18.
Таблица 1.18
Из этой таблицы видно, что число различных двоичных наборов длины
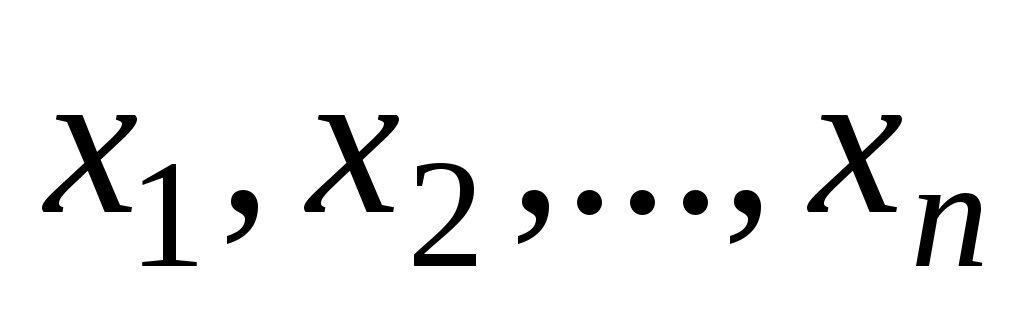 конечно и равно
конечно и равно 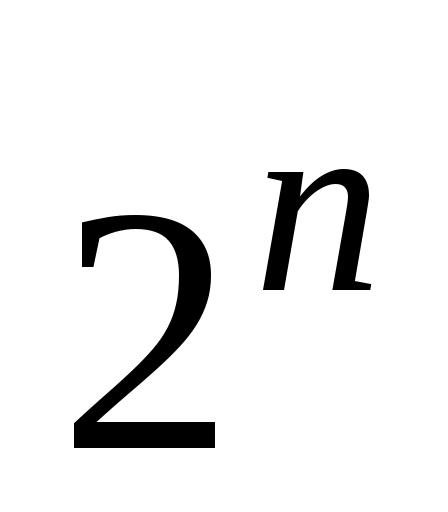 .
.
Ясно, что тавтологии и тождественно ложные функции алгебры логики представляют собой постоянные функции, а две равносильные формулы выражают одну и ту же функцию. Каждая функция определяется таблицей истинности, состоящей из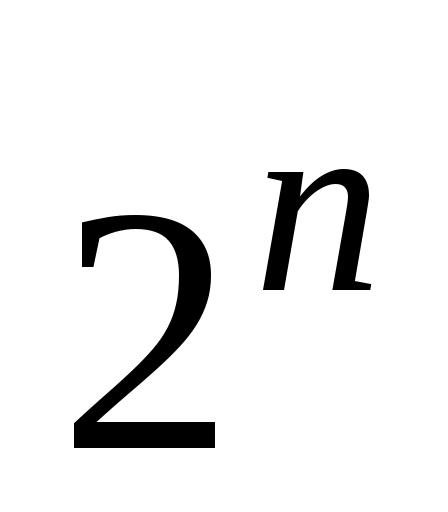 строк, то есть принимает
строк, то есть принимает 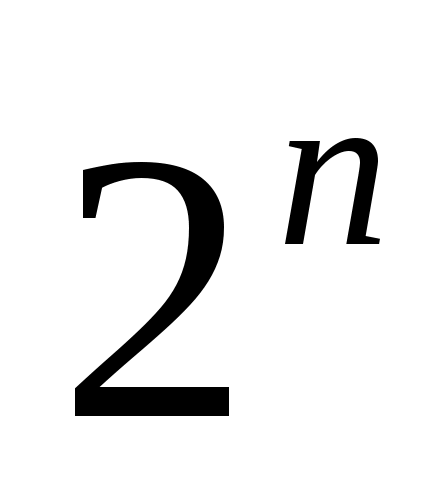 значений (каждое 0 или 1). Общее число наборов из 0 и 1 длины
значений (каждое 0 или 1). Общее число наборов из 0 и 1 длины 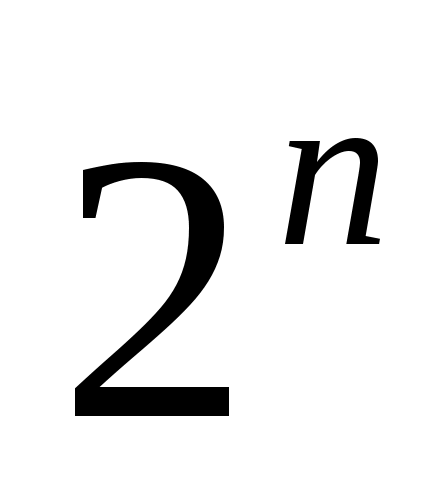 равно
равно 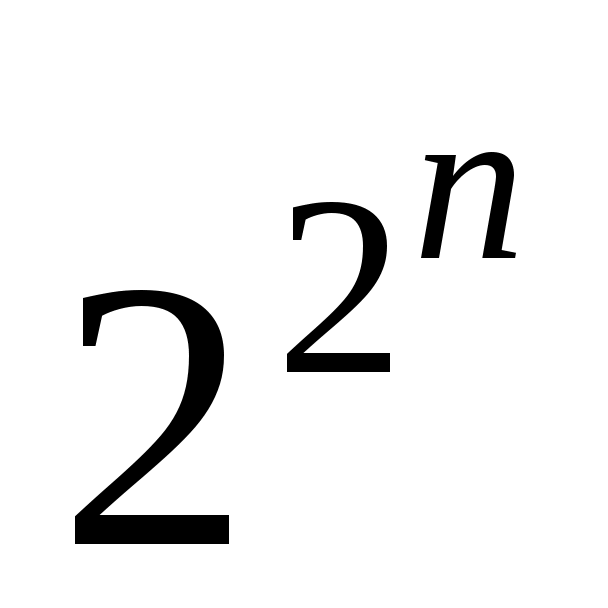 Это число равно числу различных функций алгебры логики
Это число равно числу различных функций алгебры логики  переменных.
переменных.
Каждой формуле алгебры логики соответствует своя функция. Если формулы и
и  эквивалентны, то соответствующие им функции равны:
эквивалентны, то соответствующие им функции равны: 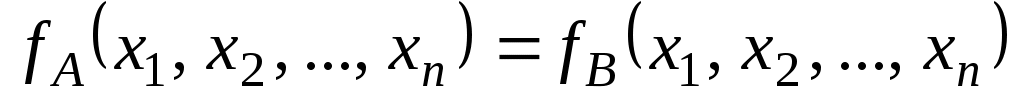 . Это значит, что при всех значениях переменных
. Это значит, что при всех значениях переменных 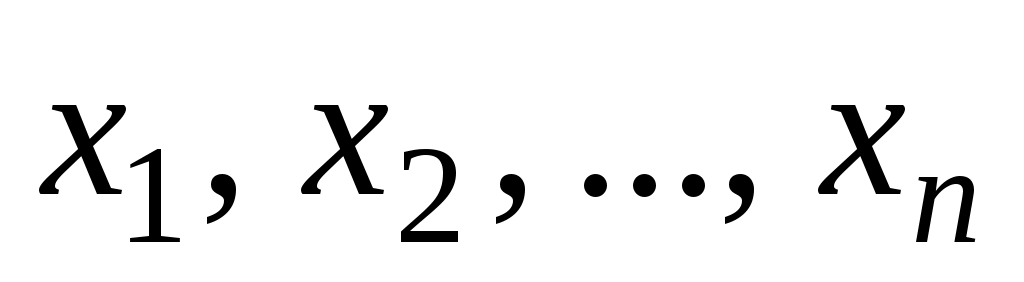 значения
значения 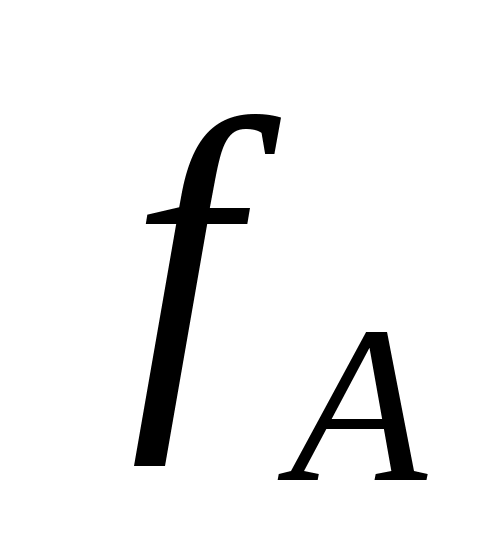 и
и 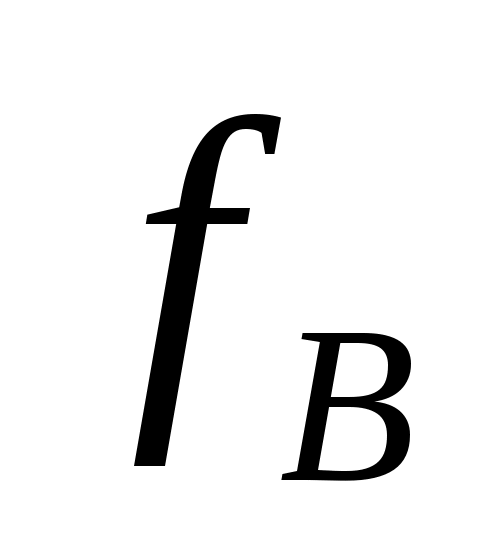 совпадают.
совпадают.
Каждая булева функция может быть путем эквивалентных преобразований приведена к двум особым формам, которые называются дизъюнктивной и конъюнктивной нормальными формами. Пусть переменные булевой функции
переменные булевой функции 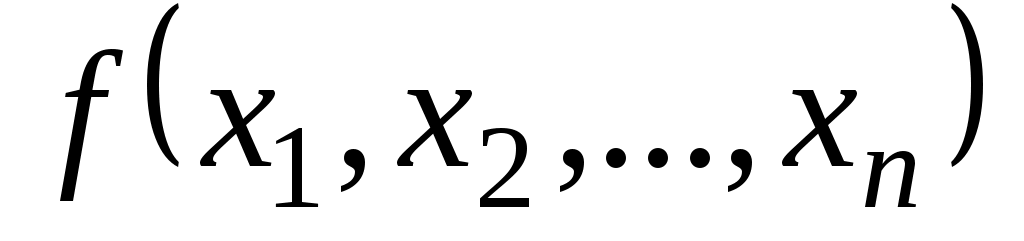 , а
, а 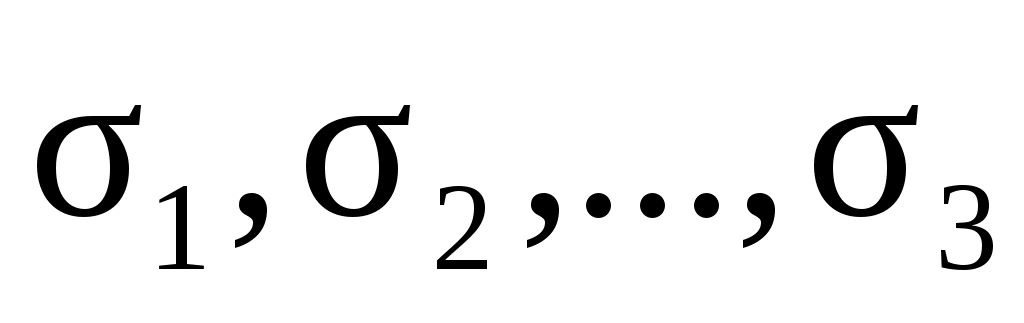
В случае импликации несоответствие между обычным пониманием истинности сложного высказывания и идеализированной точкой зрения алгебры высказываний еще заметнее, чем для других логических операций. Здесь истинность импликации в некоторой ситуации означает лишь, что если в этой ситуации истинна посылка, то истинно и заключение.
Эквиваленция (эквивалентность, логическая эквивалентность). Эквиваленцией двух высказываний
Таблица 1.17
-



1
1
1
1
0
0
0
1
0
0
0
1
С помощью логических операций над высказываниями можно строить различные новые, более сложные высказывания. Всякое сложное высказывание, которое может быть получено из элементарных высказываний с помощью логических связок, называется формулой алгебры логики. Формулы алгебры логики обозначаются большими буквами латинского алфавита
Для любых формул
-
Основные равносильности:
-
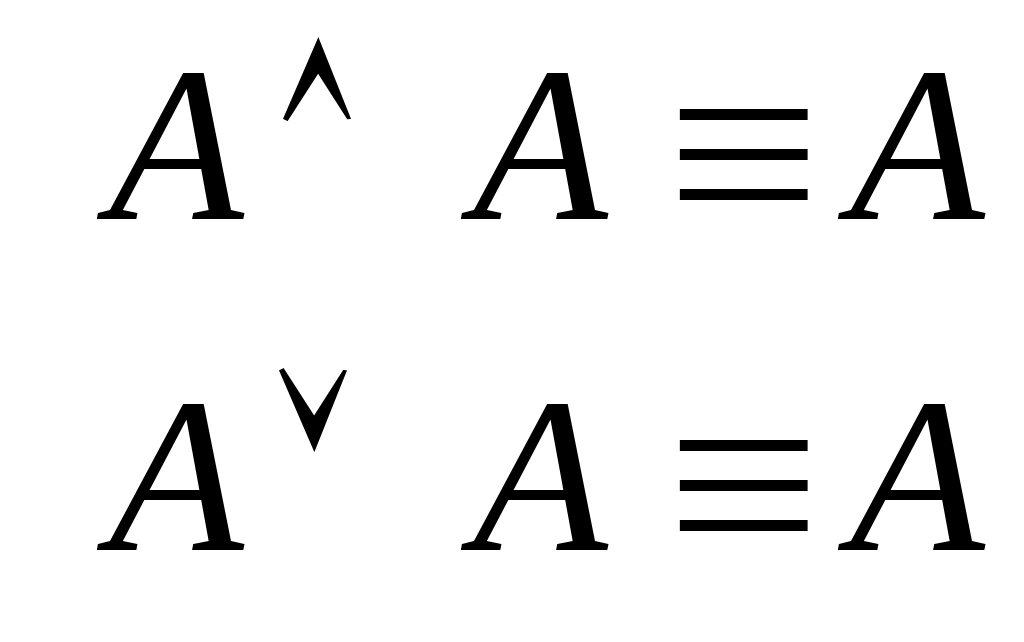 (законы идемпотентности конъюнкции и дизъюнкции);
(законы идемпотентности конъюнкции и дизъюнкции);
-
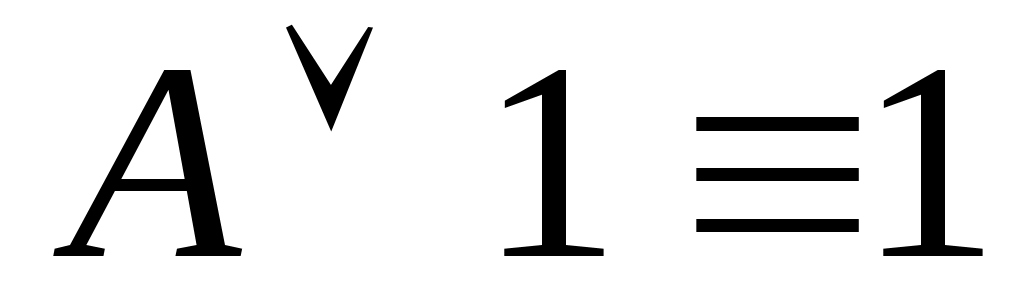 ;
; -
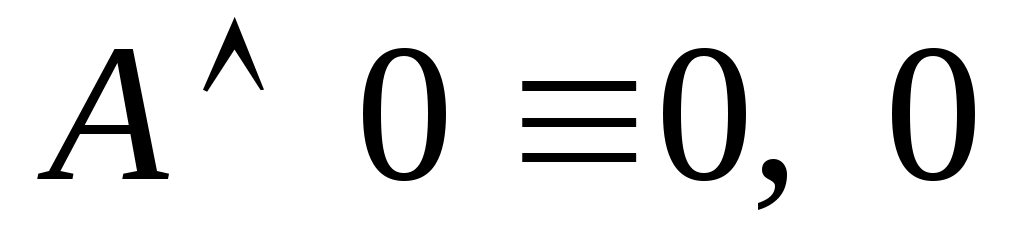 — ложь,
— ложь, -
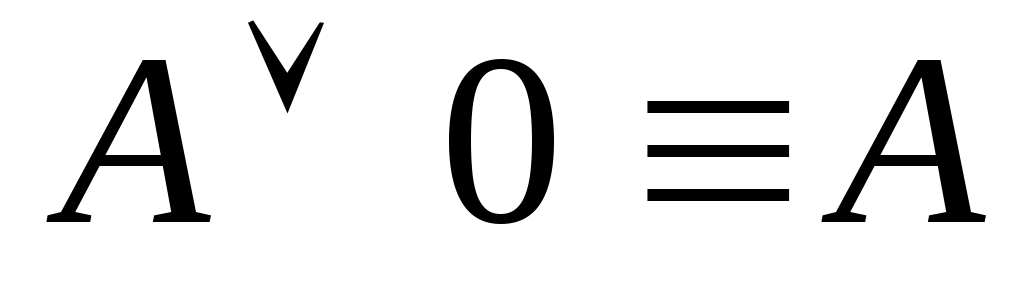 ;
; -
 (закон противоречия); (1.13.1)
(закон противоречия); (1.13.1) -
 (закон исключенного третьего);
(закон исключенного третьего); -
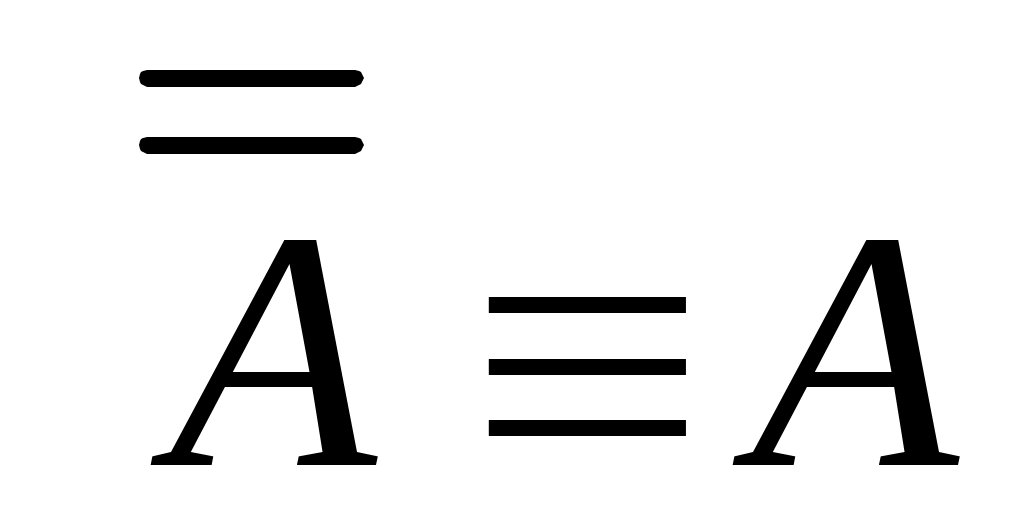 (закон снятия двойного отрицания);
(закон снятия двойного отрицания); -
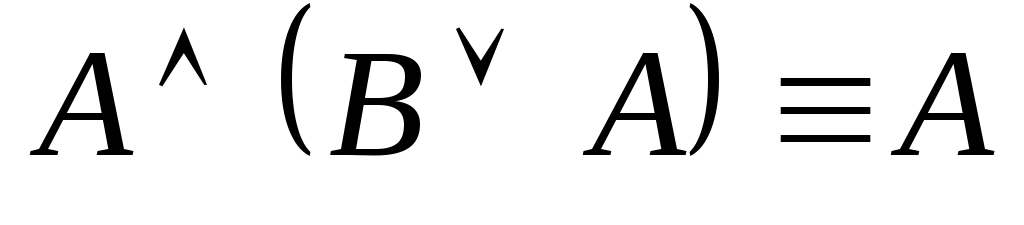 (первый закон поглощения);
(первый закон поглощения); -
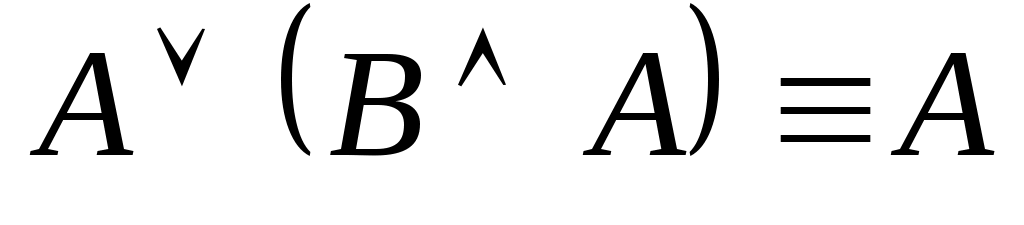 (второй закон поглощения);
(второй закон поглощения); -
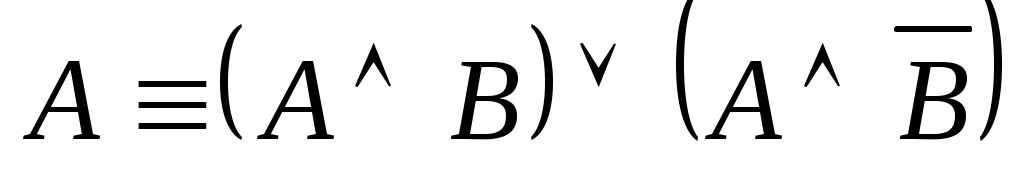 (первая формула расщепления);
(первая формула расщепления); -
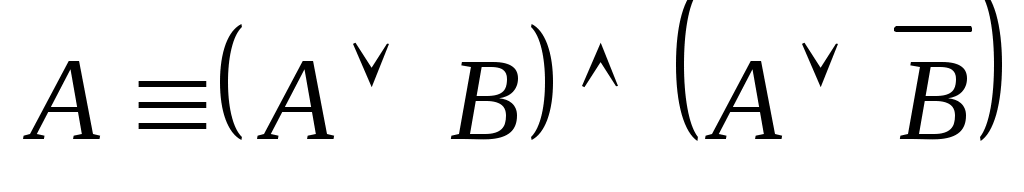 (вторая формула расщепления).
(вторая формула расщепления).
Все эти соотношения легко проверяются по таблицам истинности.
-
Равносильности, выражающие одни логические операции через другие:
-
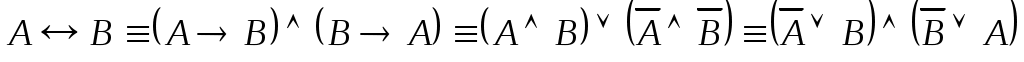 (основная формула доказательств теорем существования);
(основная формула доказательств теорем существования); -
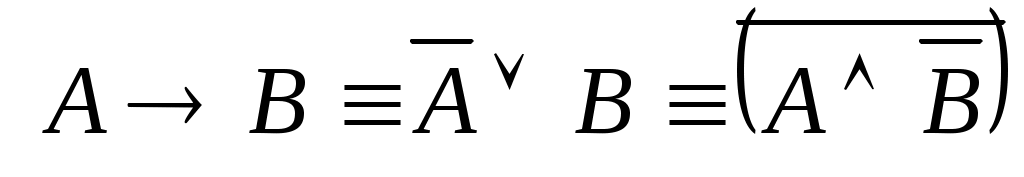 ;
; -
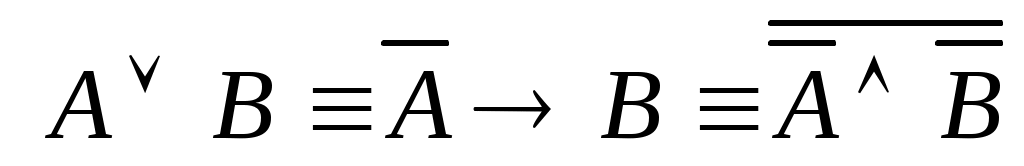 ;
; -
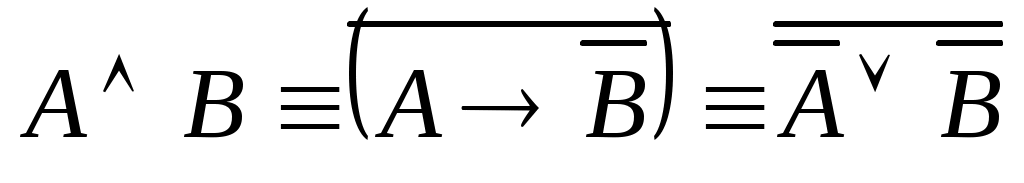 ; (1.13.2)
; (1.13.2) -
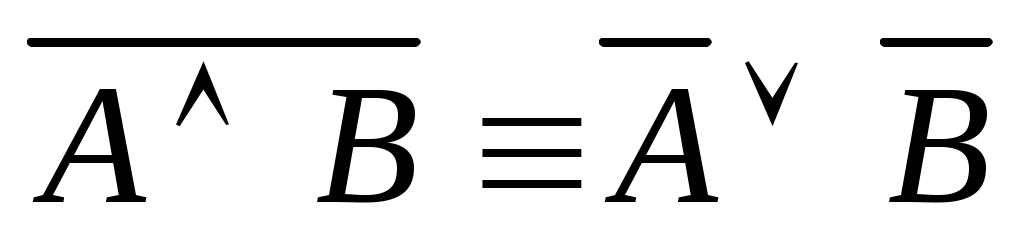 (первый закон де Моргана)4;
(первый закон де Моргана)4; -
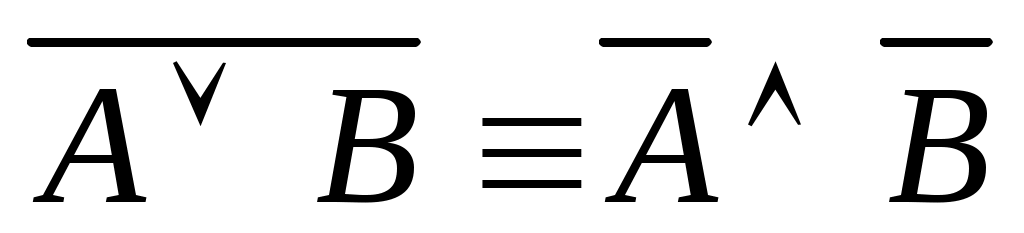 - (второй закон де Моргана);,
- (второй закон де Моргана);, -
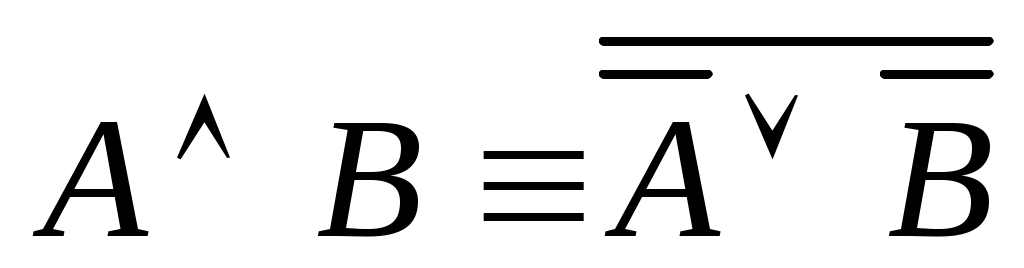 ;
; -
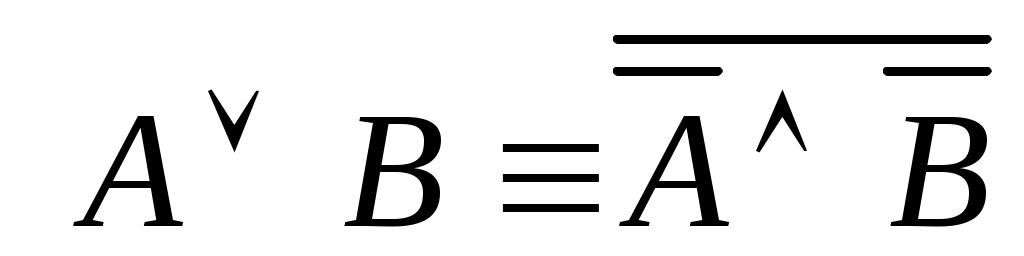 .
.
Именно из равносильностей этой группы формул следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.
-
Равносильности, выражающие основные законы алгебры логики:
-
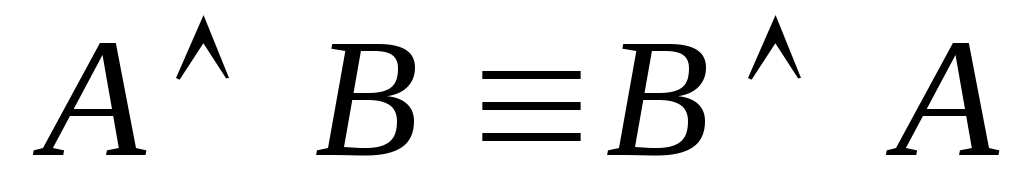 (коммутативный закон конъюнкции);
(коммутативный закон конъюнкции); -
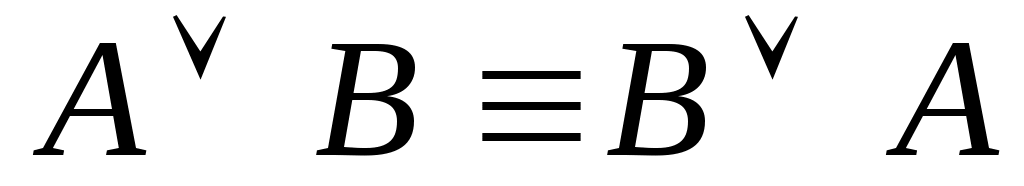 (коммутативный закон дизъюнкции);
(коммутативный закон дизъюнкции); -
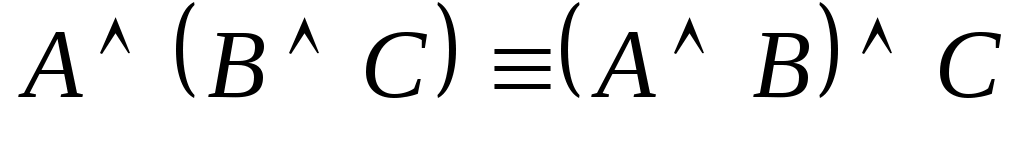 (ассоциативность конъюнкции); (1.13.3)
(ассоциативность конъюнкции); (1.13.3) -
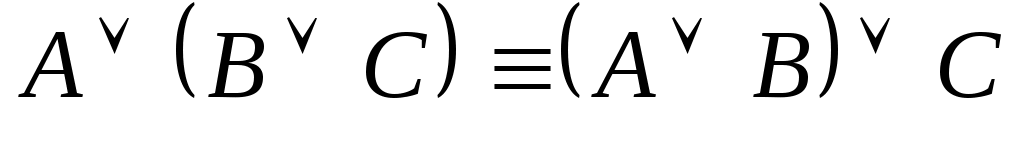 (ассоциативность дизъюнкции);
(ассоциативность дизъюнкции); -
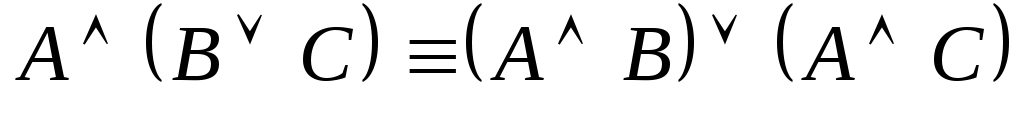 (дистрибутивность конъюнкции относительно дизъюнкции);
(дистрибутивность конъюнкции относительно дизъюнкции); -
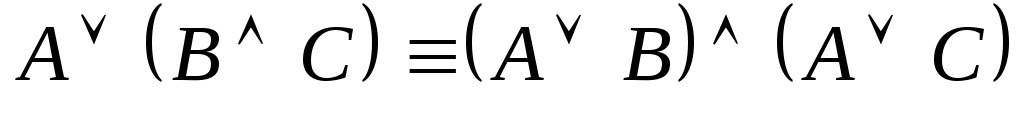 (дистрибутивность дизъюнкции относительно конъюнкции).
(дистрибутивность дизъюнкции относительно конъюнкции).
Формула
тождественно ложной или противоречивой, если она равна 0 при всех значениях входящих в нее переменных.
Формула алгебры логики является функцией входящих в нее элементарных высказываний, ее аргументы принимают два значения 0 и 1, при этом значение формулы может быть равно 0 или 1.
Функцией алгебры логики
Функция
Таблица 1.18
-
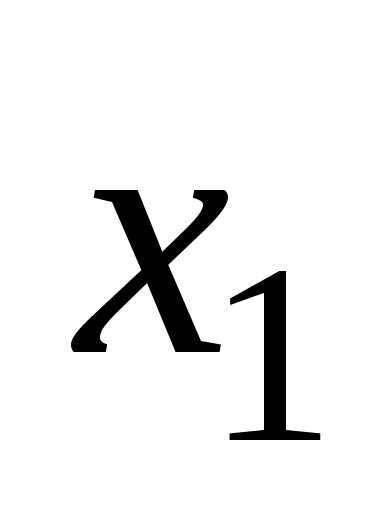
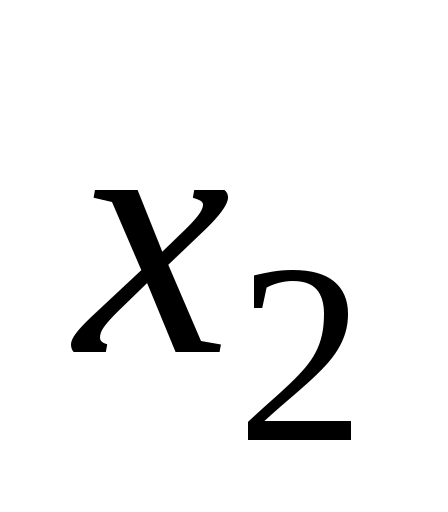
…
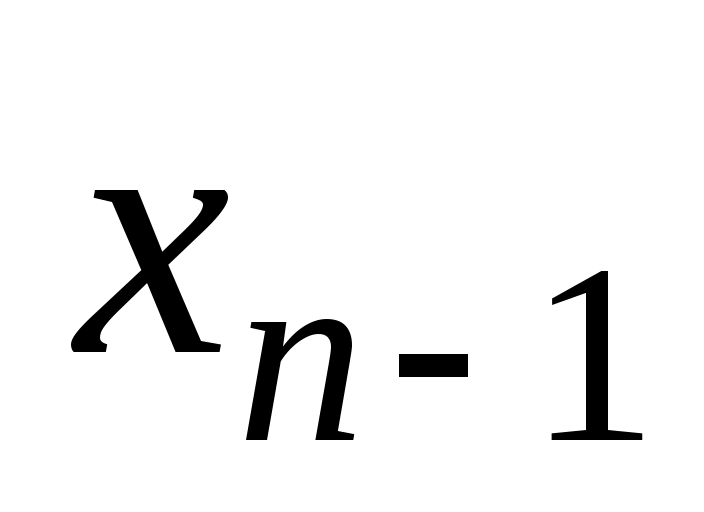
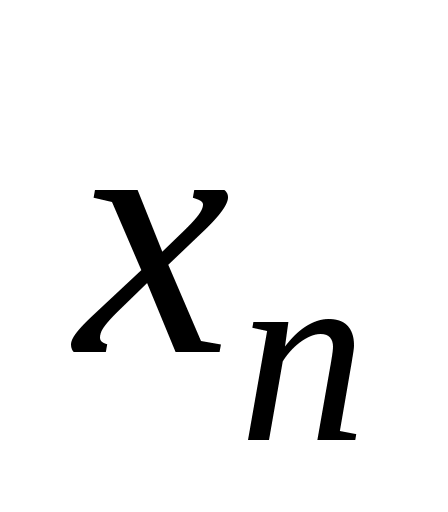
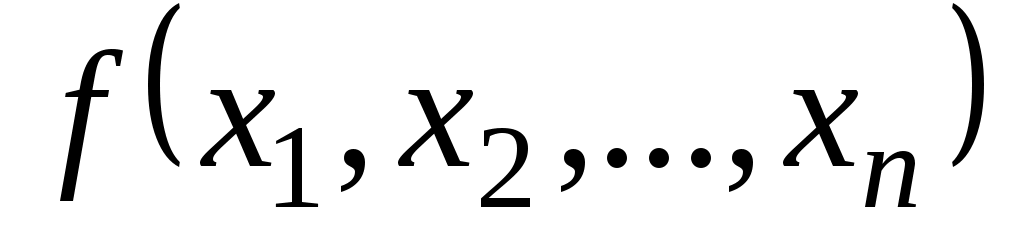
0
0
…
0
0
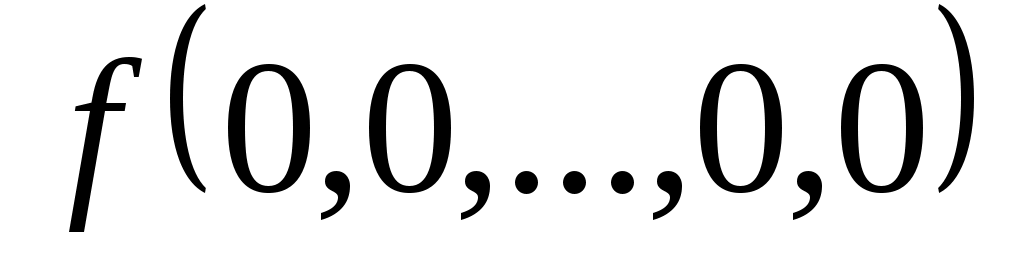
1
0
…
0
0
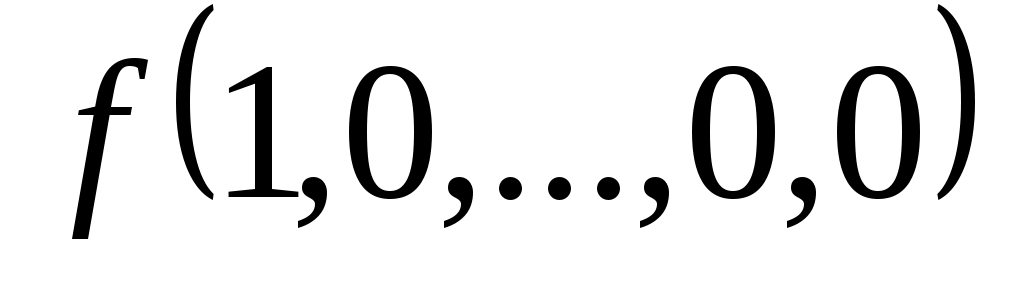
…
…
…
…
…
…
1
1
1
1
0
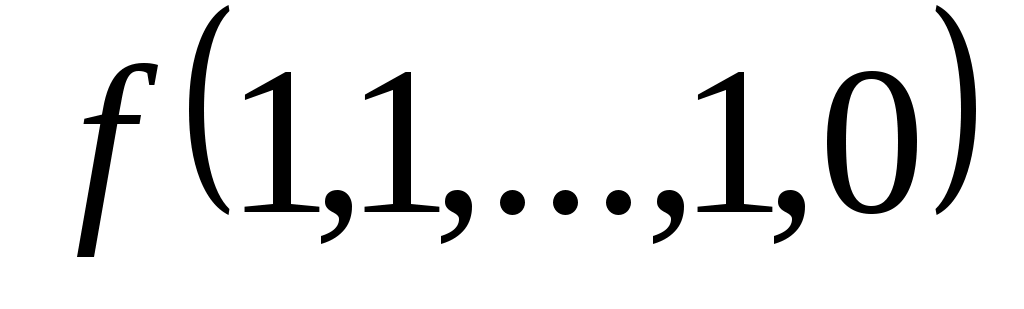
1
1
1
1
1
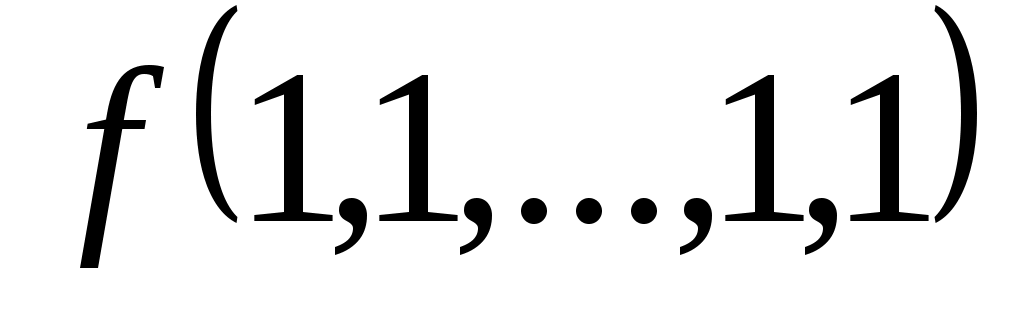
Из этой таблицы видно, что число различных двоичных наборов длины
Ясно, что тавтологии и тождественно ложные функции алгебры логики представляют собой постоянные функции, а две равносильные формулы выражают одну и ту же функцию. Каждая функция определяется таблицей истинности, состоящей из
Каждой формуле алгебры логики соответствует своя функция. Если формулы
Каждая булева функция может быть путем эквивалентных преобразований приведена к двум особым формам, которые называются дизъюнктивной и конъюнктивной нормальными формами. Пусть