Файл: Чувашский государственный педагогический университет им. И. Я. Яковлева.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 106
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ответ: , если
, если .
Глава 3. Методика применения математического пакета GeoGebra в школьном курсе планиметрии
§1. Примерный план-конспект урока с применением программы GeoGebra
Тема урока: Теорема Пифагора
Урок разработан с использованием интерактивной геометрической среды Geogebra, применение нестандартных методов обучения, ИКТ – технологий.
Изучить теорему Пифагора, с применением программы Geogebra, расширить круг геометрических задач, решаемых школьниками.
Образовательная: создать условия для усвоения теоремы Пифагора и привития навыков вычисления неизвестной стороны прямоугольного треугольника по двум известным; способствовать овладению навыками применения теоремы Пифагора к решению простейших задач при помощи геометрической среды Geogebra.
Развивающая: способствовать развитию способности к сопоставлению, наблюдательности, внимания; развитие способности к аналитико-синтетическому мышлению, расширение кругозора.
Воспитательная: формирование потребности в знаниях, интереса к математике.
Знать: Теорему Пифагора.
Уметь: доказывать теорему Пифагора и находить ее применение при решении задач и с применением геометрической среды Geogebra.
Обучение ведется по учебнику Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк И.И. Геометрия 7-9 . Соответствующая программа предполагает, что материал является для учащихся новым.
Краткий анализ урока
Данный урок является уроком изучения новых знаний по геометрии в 8 классе, направленный на достижение определенных результатов – изучение теоремы Пифагора, позволяющей существенно расширить круг задач, решаемых школьниками, а так же начальное использование современной динамической среды GeoGebra, т.е. применение нестандартных методов обучения, которые, несомненно, повышают интерес к предмету. Данная тема требует от учащихся хорошей теоретической подготовки.
Структура урока направлена на создание благоприятных условий для изучения этой темы. Для повышения эффективности урока вводный этап активизации знаний организован в виде построения рисунков в программе GeoGebra , что дает учащимся ярко и образно повторить изученный материал. Хотелось бы отметить явный интерес учеников, в связи с нестандартными, введения в урок, технологий, т.е. программы GeoGebra. Она готовит их к изучению нового материала, позволяет быстро включиться в работу. В результате выполнения практической работы по группам учащиеся приходят к выводу, что , и тогда рассматривается доказательство теоремы Пифагора с использование электронных образовательных ресурсов. Во второй части урока идет закрепление изученного, применение теоремы Пифагора при решении задач, сначала более простых, а потом более сложных с использованием электронных образовательных ресурсов.
Приложение 1
Пошаговое построение (Рис. 31)
Таблица 8
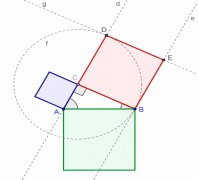
Рис. 31
Повышение построения (Рис 32)
Вставьте статический и динамический текст в вашу конструкцию, которая помогает понять теорему Пифагора .
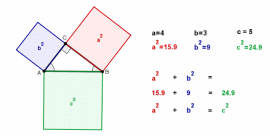
Рис. 32
§2. Анализ эффективности применения математического пакета GeoGebra в школьном курсе планиметрии
Для анализа эффективности применения программы GeoGebra было исследовано 2 урока по геометрии в СОШ № 59 г. Чебоксары, во время прохождения активной педагогической практики.
Цель состоит в том, чтобы доказать необходимость внедрения математического пакета GeoGebra в решении планиметрических задач на уроках геометрии, а так же значимость этого пакета в модернизации математического образования.
В исследовании участвовал 11 «а» класс, в котором 22 ученика. Было проведено 2 урока геометрии по решению планиметрических задач, но различным способом. В первом случае традиционный урок, во втором случае с применением программы GeoGebra.
На первом уроке ученики решали планиметрические задачи типа 16 задачи (С4) традиционным образом. Один ученик был вызван к доске, остальные решали задачи на местах. Хотелось бы отметить следующее: во-первых: на этапе изображения чертежа уже возникали некоторые сложности, ученику приходилось несколько раз стирать чертеж, дабы максимально приблизить его к правильному, во-вторых: не все ученики подключались к работе, так как правильный рисунок и решение были на доске, в-третьих: было очень сложно держать внимание учеников на конкретной задаче.
На втором уроке геометрии для решения задач по планиметрии ученики воспользовались математическим пакетом GeoGebra. Кабинет располагал нужным количеством ПК, поэтому это очень помогло сделать наиболее точные выводы. Интерфейс при изучении интуитивно понятный, а потому не вызвал никаких затруднений при изучении. Ученики с большим интересом выполняли рисунки в GeoGebra. Решая задачи при помощи программы, ученики намного быстрее находили пути решения. Так же никто не пытался списывать, все были вовлечены в работу, если же возникали вопросы, сообща помогали друг другу.
Следующим этапам исследования был опрос. Очень важным было мнение самих испытуемых, т.е. учеников. Опрос был анонимный, каждому ученику было предложено 3 вопроса, оценка по 5 бальной шкале (таб. 8):
, если .
Глава 3. Методика применения математического пакета GeoGebra в школьном курсе планиметрии
§1. Примерный план-конспект урока с применением программы GeoGebra
Тема урока: Теорема Пифагора
| | Предмет | Геометрия |
| | Класс | 8 |
| | Тема и номер урока в теме | Теорема Пифагора № 1 |
| | Базовый учебник | Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк И.И. Геометрия 7-9 учебник для 7-9 классов средней школы |
-
Технология
Урок разработан с использованием интерактивной геометрической среды Geogebra, применение нестандартных методов обучения, ИКТ – технологий.
-
Цель урока
Изучить теорему Пифагора, с применением программы Geogebra, расширить круг геометрических задач, решаемых школьниками.
-
Задачи
Образовательная: создать условия для усвоения теоремы Пифагора и привития навыков вычисления неизвестной стороны прямоугольного треугольника по двум известным; способствовать овладению навыками применения теоремы Пифагора к решению простейших задач при помощи геометрической среды Geogebra.
Развивающая: способствовать развитию способности к сопоставлению, наблюдательности, внимания; развитие способности к аналитико-синтетическому мышлению, расширение кругозора.
Воспитательная: формирование потребности в знаниях, интереса к математике.
-
Предметные результаты:
Знать: Теорему Пифагора.
Уметь: доказывать теорему Пифагора и находить ее применение при решении задач и с применением геометрической среды Geogebra.
-
Тип урока: формирование новых знаний и умений. -
Формы работы учащихся: фронтальная, индивидуальная, групповая.
-
Необходимое техническое оборудование: компьютер, интерактивная геометрическая среда Geogebra, презентация, мультимедийный проектор. -
Структура и ход урока:
Обучение ведется по учебнику Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк И.И. Геометрия 7-9 . Соответствующая программа предполагает, что материал является для учащихся новым.
| № | Этап урока | Название используемых ЭОР (с указанием порядкового номера из Таблицы 2) | Деятельность учителя (с указанием действий с ЭОР, например, демонстрация) | Деятельность ученика | Время (в мин.) |
| 1 | 2 | 3 | 5 | 6 | 7 |
| 1 | Организационный момент | | Приветствует обучающихся, проверяет их готовность к уроку, создает эмоциональный настрой. | Приветствуют учителя, проверяют свою готовность к уроку | 1 |
| 2 | Актуализация знаний учащихся, полученных ими по теме «Площадь». | Ресурс №1 Площадь многоугольника  | Формулирует задания на повторение материала по теме: Площадь, демонстрируя создание изображений в программе Geogebra, отмечает степень вовлеченности учащихся в работу, при необходимости уточняет ответы учащихся. | Учащиеся отвечают на поставленные вопросы, слушают ответы своих одноклассников, по необходимости делают поправки и дополнения (текущий контроль в форме фронтального опроса). Учащиеся осуществляют самопроверку. | 10 |
| 3 | Формирование новых знаний: Изучение теоремы Пифагора | Ресурс №2 Наглядное представление теоремы Пифагора  Ресурс №3 Доказательство теоремы Пифагора  и иллюстрация в программе Geogebra 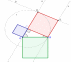 Рис. 31 | Организует работу по группам, выдвигает проблему, побуждает к высказыванию собственного мнения, помогает сделать верные выводы, формирует представление учащихся о теореме Пифагора, демонстрируя ресурс №2, что равенство, а2+в2=с2 справедливо для любого прямоугольного треугольника. Учитель подводит учащихся к изучению нового материала. Учитель организует просмотр видеофрагмента доказательство теоремы Пифагора, организует беседу по уточнению и конкретизации первичных знаний, делает чертёж программе Geogebra (Приложение 1). | Учащиеся по группам выполняют практическую работу на построение прямоугольных треугольников с катетами 3 и 4 см; 5 и 12 см; 6 и 8 см, а затем проверяют равенство, а2+в2=с2. Анализируют полученный результат и высказывают свои предположения Учащиеся изучают доказательство теоремы при помощи видеофрагмента и иллюстрации рисунка в программе Geogebra, обсуждают этапы доказательства теоремы, оформляют доказательство в тетради. | 15 |
| 4 | Закрепление знаний: применение теоремы Пифагора при решении задач. | Ресурс № 4 Устные упражнения. Теорема Пифагора  | Учитель предлагает учащимся решить задачи на применение теоремы Пифагора так же выборочно и с применением программы Geogebra. Организует обсуждение способов решения, учитель оказывает индивидуальную помощь по необходимости. | Учащиеся высказывают свое мнение и записывают решение задачи в тетради. По желание несколько учеников сидят за ПК и выполняют при помощи программы Geogebra. | 13 |
| 5 | Историческая справка | Ресурс №5 Еще один способ доказательства теоремы. Фрагменты 2 и 3. | Учитель предлагает учащимся еще одно из доказательств теоремы. | Учащиеся слушают и смотрят видеофрагменты | 4 |
| 6 | Домашнее задание | Ресурс №6 Домашнее задание.  | Акцентирует внимание на конечных результатах учебной деятельности обучающихся на уроке, дает комментарий к домашнему заданию. | Формулируют конечный результат своей работы на уроке. Называют основные понятия нового материала и как они их усвоили (что получилось, что не получилось и почему) Учащиеся записывают домашнее задание. | 2 |
Краткий анализ урока
Данный урок является уроком изучения новых знаний по геометрии в 8 классе, направленный на достижение определенных результатов – изучение теоремы Пифагора, позволяющей существенно расширить круг задач, решаемых школьниками, а так же начальное использование современной динамической среды GeoGebra, т.е. применение нестандартных методов обучения, которые, несомненно, повышают интерес к предмету. Данная тема требует от учащихся хорошей теоретической подготовки.
Структура урока направлена на создание благоприятных условий для изучения этой темы. Для повышения эффективности урока вводный этап активизации знаний организован в виде построения рисунков в программе GeoGebra , что дает учащимся ярко и образно повторить изученный материал. Хотелось бы отметить явный интерес учеников, в связи с нестандартными, введения в урок, технологий, т.е. программы GeoGebra. Она готовит их к изучению нового материала, позволяет быстро включиться в работу. В результате выполнения практической работы по группам учащиеся приходят к выводу, что , и тогда рассматривается доказательство теоремы Пифагора с использование электронных образовательных ресурсов. Во второй части урока идет закрепление изученного, применение теоремы Пифагора при решении задач, сначала более простых, а потом более сложных с использованием электронных образовательных ресурсов.
Приложение 1
Пошаговое построение (Рис. 31)
Таблица 8
| № | Иконка GeoGebra | Построение |
| 1 |  | Создайте отрезок с концами . |
| 2 |  | Создайте полуокружность через точки и . |
| 3 |   | Создайте новую точку на полуокружности. Подсказка: проверьте, если точка на самом деле лежит на дуге, перетащив его с помощью мыши. |
| 4 |  | Скройте отрезок и полуокружность. |
| 5 |  | Постройте треугольник в направлении против часовой стрелки. |
| 6 |  | Переименуйте стороны треугольника и . |
| 7 |  | Создайте внутренние углы треугольника. Подсказка: нажмите кнопку в центре многоугольника для создания всех углов. |
| 8 |  | Перетащите точку , чтобы проверить, правильны ли ваши построения. |
| 9 |  | Создайте перпендикулярную прямую к отрезку через точку . |
| 10 |  | Создайте перпендикулярную прямую к отрезку через точку . |
| 11 |  | Создайте окружность с центром в точке через точку . |
| 12 |  | Пересечение окружности и перпендикулярной прямой , чтобы получить точку пересечения . |
| 13 |  | Создайте параллельную прямую к отрезку , через точку . |
| 14 |  | Создайте точку пересечения прямых и . |
| 15 |  | Создайте квадрат . |
| 16 |  | Скройте вспомогательные линии и окружности. |
| 17 | | Повторите шаги с 8 по 15 для боковой треугольника. |
| 18 | | Повторите шаги с 8 по 15 для боковой треугольника. |
| 19 |  | Перетащите вершины прямоугольного треугольника, чтобы проверить правильно ли построен квадрат. |
| 20 | | Повысьте конструкцию с помощью настройки стиля. |

Рис. 31
Повышение построения (Рис 32)
Вставьте статический и динамический текст в вашу конструкцию, которая помогает понять теорему Пифагора .

Рис. 32
| 21 |  | Создайте середины всех трех квадратов. Подсказка: щелкните по диагонали противоположных вершин каждого квадрата. |
| 22 |  | Вставьте статические Надпись 1: и приложите его к середине соответствующей площади. |
| 23 |  | Вставьте статические Надпись 2: и приложите его к середине соответствующей площади. |
| 24 |  | Вставьте статические Надпись 3: и приложите его к середине соответствующей площади. |
| 25 |  | Скройте середины квадратов. |
| 26 |  | Отформатируйте текст в соответствии с цветом соответствующих квадратов. |
| 27 |  | Вставьте текст, который описывает теорему Пифагора. |
1 2 3 4 5 6 7
§2. Анализ эффективности применения математического пакета GeoGebra в школьном курсе планиметрии
Для анализа эффективности применения программы GeoGebra было исследовано 2 урока по геометрии в СОШ № 59 г. Чебоксары, во время прохождения активной педагогической практики.
Цель состоит в том, чтобы доказать необходимость внедрения математического пакета GeoGebra в решении планиметрических задач на уроках геометрии, а так же значимость этого пакета в модернизации математического образования.
В исследовании участвовал 11 «а» класс, в котором 22 ученика. Было проведено 2 урока геометрии по решению планиметрических задач, но различным способом. В первом случае традиционный урок, во втором случае с применением программы GeoGebra.
На первом уроке ученики решали планиметрические задачи типа 16 задачи (С4) традиционным образом. Один ученик был вызван к доске, остальные решали задачи на местах. Хотелось бы отметить следующее: во-первых: на этапе изображения чертежа уже возникали некоторые сложности, ученику приходилось несколько раз стирать чертеж, дабы максимально приблизить его к правильному, во-вторых: не все ученики подключались к работе, так как правильный рисунок и решение были на доске, в-третьих: было очень сложно держать внимание учеников на конкретной задаче.
На втором уроке геометрии для решения задач по планиметрии ученики воспользовались математическим пакетом GeoGebra. Кабинет располагал нужным количеством ПК, поэтому это очень помогло сделать наиболее точные выводы. Интерфейс при изучении интуитивно понятный, а потому не вызвал никаких затруднений при изучении. Ученики с большим интересом выполняли рисунки в GeoGebra. Решая задачи при помощи программы, ученики намного быстрее находили пути решения. Так же никто не пытался списывать, все были вовлечены в работу, если же возникали вопросы, сообща помогали друг другу.
Следующим этапам исследования был опрос. Очень важным было мнение самих испытуемых, т.е. учеников. Опрос был анонимный, каждому ученику было предложено 3 вопроса, оценка по 5 бальной шкале (таб. 8):