Файл: Чувашский государственный педагогический университет им. И. Я. Яковлева.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 108
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.2. Квадрат
Задача 2. Вокруг квадрата описан параллелограмм. Докажите, что перпендикуляры, опущенные из вершин параллелограмма на стороны квадрата, образуют квадрат.
Шаги создания чертежа в GeoGebra (таб. 2):
Таблица 2
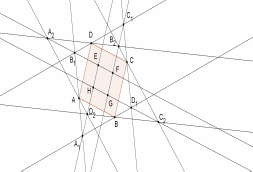
Рис. 16
2.3. Расположение точек на прямой
Задача 3. (ЕГЭ, 2010) Через середину стороны квадрата проведена прямая, пересекающая прямые и в точках и соответственно и образующая с прямой угол , . Найдите площадь треугольника , если сторона квадрата равна 4.
Решение. 1-й случай: пусть прямая, проходящая через середину сторона , пересекает отрезок и продолжение отрезка за точку (рис. 3).
Тогда
Шаги построения в GeoGebre (таб. 3):
Таблица 3
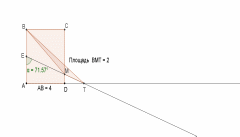
Рис.17
2-й случай: пусть прямая, проходящая через середину стороны , пересекает отрезок и продолжение отрезка за точку (рис. 18). Тогда
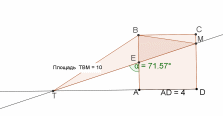
Рис. 18
Ответ: 2 и 10.
2.4. Расположение точек внепрямой
Задача 4. (ЕГЭ, 2010) В окружность радиуса вписана трапеция с основаниями 8 и . Найдите длину диагонали трапеции.
Решение. Трапеция, вписанная в окружность, является равнобедренной.
1-й случай: пусть центр окружности лежит вне трапеции (рис. 19). Так как прямая, проходящая через центр окружности и перпендикулярная хорде, делит эту хорду пополам, то и. Из прямоугольных треугольников и FD находим
и
Высота трапеции равна длине отрезка. Длина отрезка равна длине средней линии .
Находим диагональ из прямоугольного треугольника
Шаги построения в GeoGebra (таб. 4):
Таблица 4
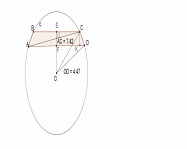
Рис. 19
2-й случай: пусть центр окружности лежит внутри трапеции (рис. 20). Высота трапеции равна длине отрезка .
Находим диагональ из прямоугольного треугольника
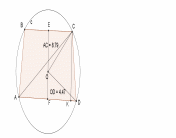
Рис. 20
2.5. Выбор некоторого элемента фигуры
Задача 5. (ЕГЭ, 2012) Дан равнобедренный треугольник с боковой стороной равной 4 углом . Внутрь треугольника вписаны две равные окружности таким образом, что окружности касаются друг друга и каждая окружность касаются двух сторон треугольника. Найдите радиус окружностей.
Решение. В данном треугольнике углы при основании, основание и высота, опущенная на основание, соответственно равны , .
Существует два рисунка, удовлетворяющих условию задачи.
1-й случай: пусть каждая из окружностей касается основания и боковой стороны (рис. 21). В этом случае каждая из этих окружностей вписывается в прямоугольный треугольник со стороной 2, 2 и 4. Рассмотрим, например, прямоугольный треугольник. Радиус вписанной в него окружности находим по формуле:
Шаги построения в GeoGebre (таб. 5):
Таблица 5
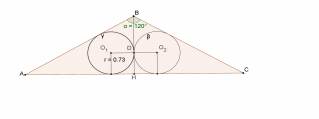
Рис. 21
2-й случай: пусть обе окружности касаются одной из боковых сторон (рис. 22). Так как центры окружностей лежат на биссектрисах, радиусы, проведенные в точку касания, перпендикулярны стороне и , то получим
Найдем по формуле
Тогда получим, Отсюда
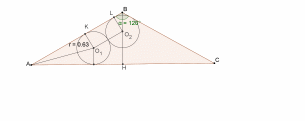
Рис.22
Задача 2. Вокруг квадрата описан параллелограмм. Докажите, что перпендикуляры, опущенные из вершин параллелограмма на стороны квадрата, образуют квадрат.
Шаги создания чертежа в GeoGebra (таб. 2):
Таблица 2
| № | Имя | Иконка GeoGebra | Определение |
| 1 | Квадрат |  | Квадрат, проходящий через точки . |
| 2 | Прямые |  | Прямая, проходящая через точки |
| 3 | Прямые |  | Прямая, проходящая через точку и параллельная . |
| 4 | Отрезки , |  | Отрезки |
| 5 | Прямые |  | Прямая, проходящая через точки . |
| 6 | Прямые |  | Прямая, проходящая через точку и параллельная . |
| 7 | Отрезки , |  | Отрезки |
| 8 | Прямые |  | Прямая, проходящая через точку , перпендикулярная . |
| 9 | Прямая |  | Прямая, проходящая через точку , перпендикулярная . |
| 10 | Прямая |  | Прямая, проходящая через точку, перпендикулярная. |
| 11 | Прямая |  | Прямая, проходящая через точку, перпендикулярная. |
| 12 | Многоугольник |  | Искомый квадрат |

Рис. 16
2.3. Расположение точек на прямой
Задача 3. (ЕГЭ, 2010) Через середину стороны квадрата проведена прямая, пересекающая прямые и в точках и соответственно и образующая с прямой угол , . Найдите площадь треугольника , если сторона квадрата равна 4.
Решение. 1-й случай: пусть прямая, проходящая через середину сторона , пересекает отрезок и продолжение отрезка за точку (рис. 3).
Тогда
Шаги построения в GeoGebre (таб. 3):
Таблица 3
| № | Имя | Иконка GeoGebra | Определение |
| 1 | Отрезок | 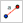 | Отрезок c длиной 4. |
| 2 | Квадрат |  | Квадрат c длиной 4. |
| 3 | Точка |  | Середина отрезка . |
| 4 | Угол |  | Угол между образующей и прямой . |
| 5 | Точка |  | Точка пересечения прямых. |
| 6 | Треугольник |  | Многоугольник через три точки . |
| 7 | Площадь треугольника |  | Указывая на многоугольник , находим ее площадь равная 2. |

Рис.17
2-й случай: пусть прямая, проходящая через середину стороны , пересекает отрезок и продолжение отрезка за точку (рис. 18). Тогда

Рис. 18
Ответ: 2 и 10.
2.4. Расположение точек внепрямой
Задача 4. (ЕГЭ, 2010) В окружность радиуса вписана трапеция с основаниями 8 и . Найдите длину диагонали трапеции.
Решение. Трапеция, вписанная в окружность, является равнобедренной.
1-й случай: пусть центр окружности лежит вне трапеции (рис. 19). Так как прямая, проходящая через центр окружности и перпендикулярная хорде, делит эту хорду пополам, то и. Из прямоугольных треугольников и FD находим
и
Высота трапеции равна длине отрезка. Длина отрезка равна длине средней линии .
Находим диагональ из прямоугольного треугольника
Шаги построения в GeoGebra (таб. 4):
Таблица 4
| № | Имя | Иконка GeoGebra | Определение |
| 1 | Отрезок |  | Отрезок c длиной. |
| 2 | Окружность |  | Окружность с радиусом . |
| 3 | Отрезок |  | Отрезок c длиной . |
| 4 | Отрезок |  | Отрезок c длиной . |
| 5 | Многоуголь-ник |  | Равнобедренная трапеция |
| 6 | Отрезок |  | Соединяем точки и находим длину диагонали . |

Рис. 19
2-й случай: пусть центр окружности лежит внутри трапеции (рис. 20). Высота трапеции равна длине отрезка .
Находим диагональ из прямоугольного треугольника

Рис. 20
2.5. Выбор некоторого элемента фигуры
Задача 5. (ЕГЭ, 2012) Дан равнобедренный треугольник с боковой стороной равной 4 углом . Внутрь треугольника вписаны две равные окружности таким образом, что окружности касаются друг друга и каждая окружность касаются двух сторон треугольника. Найдите радиус окружностей.
Решение. В данном треугольнике углы при основании, основание и высота, опущенная на основание, соответственно равны , .
Существует два рисунка, удовлетворяющих условию задачи.
1-й случай: пусть каждая из окружностей касается основания и боковой стороны (рис. 21). В этом случае каждая из этих окружностей вписывается в прямоугольный треугольник со стороной 2, 2 и 4. Рассмотрим, например, прямоугольный треугольник. Радиус вписанной в него окружности находим по формуле:
Шаги построения в GeoGebre (таб. 5):
Таблица 5
| № | Имя | Иконка GeoGebra | Определение |
| 1 | Окружность |  | Окружность с радиусом . |
| 2 | Угол |  | Угол между радиусами и . |
| 3 | Многоугольник |  | Равнобедренный треугольник . |
| 4 | Прямая |  | Прямая через , перпендикулярная . |
| 5 | Точка |  | Точка пересечения прямыхи. |
| 4 | Отрезок |  | Соединим точки . |
| 5 | Точка |  | Точка пересечения перпендикуляра и прямой . |
| 6 | Точка |  | Точка пересечения биссектрис треугольника |
| 7 | Окружность |  | Окружность по центру и точке |
| 8 | Точка |  | Точка пересечения биссектрис треугольника . |
| 9 | Окружность |  | Окружность по центру и точке |
| 10 | Отрезок |  | Отрезок 0,73 |

Рис. 21
2-й случай: пусть обе окружности касаются одной из боковых сторон (рис. 22). Так как центры окружностей лежат на биссектрисах, радиусы, проведенные в точку касания, перпендикулярны стороне и , то получим
Найдем по формуле
Тогда получим, Отсюда

Рис.22
1 2 3 4 5 6 7