Файл: Чувашский государственный педагогический университет им. И. Я. Яковлева.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 103
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ответ:;.
2.6. Выбор плоской фигуры
Задача 6. (ЕГЭ, 2011) Через вершину правильного шестиугольника проведена прямая, пересекающая диагональ в точке . Известно, что эта прямая разбивает шестиугольник на части, площади которых относятся как . Найдите отношение .
Решение. Пусть – центр правильного шестиугольника , – его площадь (рис. 23). Тогда
1-й случай: пусть точкарасположена между точками и (рис. 24). Пусть прямая пересекает сторону в точке . Тогда
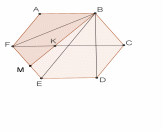
Рис.23
Треугольники и имеют общую высоту, опущенную из вершины . Поэтому
Треугольник подобен треугольнику , поэтому
2-й случай: пусть точка расположена между точками и(рис. 24). Пусть прямая пересекает сторону в точке .
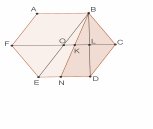
Рис. 24
Тогда
Пусть диагонали и пересекаются в точке . Тогда – середина .
Треугольники и имеют общую высоту, опущенную из вершины . Поэтому
Значит, и
Пусть , , тогда, , , , .
Отсюда
Ответ: или .
2.7. Взаимное расположение окружностей
Задача 7. (ЕГЭ, 2012) Точка – центр правильного шестиугольника со стороной 7. Найдите радиус окружности касающейся окружностей, описанных около треугольника
Решение. Пусть точка – центр правильного шестиугольника со стороной (рис. 25). Радиус окружностей, описанных около треугольников , , равен .
Рассмотрим, например, треугольник .
Его сторона (диагональ правильного шестиугольника со стороной ), . Из теоремы синусов для треугольника получаем
Отсюда .
Рассмотрим возможные положения окружностей удовлетворяющих условию задачи.
1-й случай: пусть искомая окружность, касается всех данных окружностей внутренним образом. В этом случае ее центр находится в точке и радиус равен (рис. 26)
Шаги построения в GeoGebre (таб. 6):
Таблица 6
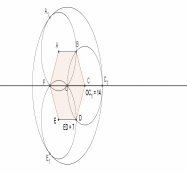
Рис. 25
2-й случай: пусть искомая окружность касается одной из окружностей (например, проходящей через точки ) внутренним образом, а двух других внешним образом (рис. 26).
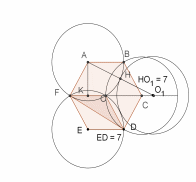
Рис 26
Пусть – центр этой окружности, а ее радиус равен Тогда, воспользуемся теоремой: точки касания и центры касающихся окружностей лежат на одной прямой и расстояние между центрами равно сумме радиусов при внешнем касании и их разности при внутреннем.
Тогда .
Рассмотрим прямоугольный треугольник , где точка – проекция точки на диагональ
В этом треугольнике
Из теоремы Пифагора получаем
Отсюда получаем
Соответственно в данной задаче при получаем два ответа и .
Ответ: 14 или 6.
Задача 8. К двум окружностям, расположенным одна вне другой, проведены одна внешняя и одна внутренняя касательные. Рассмотрим две прямые, каждая из которых проходит через точки касания, принадлежащие одной из окружностей. Докажите, что точка пересечения этих прямых расположена на прямой, соединяющей центры окружностей.
Доказательство. Сделаем построение в GeoGebra (рис. 27) Обозначим центры окружностей через и . Внешняя касательная касается первой окружности в точке , а второй окружности в точке ; внутренняя касательная касается первой окружности в точке , а второй окружности в точке .
Пусть прямые и пересекают прямую в точках и соответственно. Надо доказать, что . Рассмотрим точки пересечения прямых и , и , исоответственно. , поэтому прямоугольные треугольники подобны, а также и . Из параллельности этих прямых получаем
Из подобия четырёхугольников получаем
Следовательно, , т. е. ч.т.д.

Рис. 27
Задача 9. (ЕГЭ, 2014 ) На гипотенузе прямоугольного треугольника опустили высоту . Из точки катеты опустили перпендикуляры и.
а) Докажите, что точки лежат на одной окружности.
б) Найдите радиус этой окружности, если .
Решение.
а) Докажем, что четырехугольник можно вписать в окружность.
Четырехугольник можно вписать в окружность, если сумма противоположных углов четырехугольника равна 180 градусов.
Шаги создания чертежа в GeoGebra (таб. 7):
Таблица 7
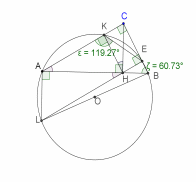
Рис. 28
Из чертежа (рис. 28) видно, что сумма противолежащих углов в четырехугольнике равна 180 градусов, . Значит, около четырехугольника можно описать окружность. (ч.т.д.)
б) Найдите радиус этой окружности, если .
Рассмотрим прямоугольный треугольник . Угол – вписанный угол, который опирается на диаметр , и, следовательно, . В этом треугольнике мы знаем катет . По условию задачи . Найдем второй катет. Для этого рассмотрим четырехугольник :
и четырехугольник – параллелограмм:
(по условию).
Итак, задача свелась к нахождению гипотенузы прямоугольного треугольника :
, отсюда .
Ответ: 6,5.
2.8. Линейные и угловые элементы треугольника
Задача 10. (ЕГЭ, 2015) Дан прямоугольный треугольник с прямым углом при вершине при вершине и углом при вершине. Точка – середина гипотенузы. Точка симметрична точке относительно прямой . Найдите угол .
Решение. Рассмотрим два случая: и .
Рассуждения, справедливые для обоих случаев:
.
Поскольку точка симметрична точке относительно прямой , то и перпендикулярна .
Значит, , , треугольники и равны.
.
.
Из прямоугольного треугольника , .
, следовательно, треугольник – равнобедренный. Угол при его вершине .
А углы при основании .
Соответственные углы , следовательно, прямые параллельны. Следовательно, .
1-й случай:.
Рассмотрим решение в GeoGebra (Рис. 29). В данном случае, , тогда .
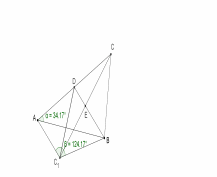
Рис. 29
2-й случай:.
Рассмотрим решение в GeoGebre (Рис. 30). В данном случае,, тогда .

Рис. 30
3-й случай: если то задача не имеет смысла, т.к. точки и совпадают.
2.6. Выбор плоской фигуры
Задача 6. (ЕГЭ, 2011) Через вершину правильного шестиугольника проведена прямая, пересекающая диагональ в точке . Известно, что эта прямая разбивает шестиугольник на части, площади которых относятся как . Найдите отношение .
Решение. Пусть – центр правильного шестиугольника , – его площадь (рис. 23). Тогда
1-й случай: пусть точкарасположена между точками и (рис. 24). Пусть прямая пересекает сторону в точке . Тогда

Рис.23
Треугольники и имеют общую высоту, опущенную из вершины . Поэтому
Треугольник подобен треугольнику , поэтому
2-й случай: пусть точка расположена между точками и(рис. 24). Пусть прямая пересекает сторону в точке .

Рис. 24
Тогда
Пусть диагонали и пересекаются в точке . Тогда – середина .
Треугольники и имеют общую высоту, опущенную из вершины . Поэтому
Значит, и
Пусть , , тогда, , , , .
Отсюда
Ответ: или .
2.7. Взаимное расположение окружностей
Задача 7. (ЕГЭ, 2012) Точка – центр правильного шестиугольника со стороной 7. Найдите радиус окружности касающейся окружностей, описанных около треугольника
Решение. Пусть точка – центр правильного шестиугольника со стороной (рис. 25). Радиус окружностей, описанных около треугольников , , равен .
Рассмотрим, например, треугольник .
Его сторона (диагональ правильного шестиугольника со стороной ), . Из теоремы синусов для треугольника получаем
Отсюда .
Рассмотрим возможные положения окружностей удовлетворяющих условию задачи.
1-й случай: пусть искомая окружность, касается всех данных окружностей внутренним образом. В этом случае ее центр находится в точке и радиус равен (рис. 26)
Шаги построения в GeoGebre (таб. 6):
Таблица 6
| № | Имя | Иконка GeoGebra | Определение |
| 1 | Отрезок |  | Отрезок c длиной . |
| 2 | Многоугольник |  | Правильный шестиугольник со стороной равной 7. |
| 3 | Точка |  | Точка пересечения диагоналей шестиугольника и, . |
| 4 | Окружность |  | Окружность через три точки . |
| 5 | Окружность |  | Окружность через три точки . |
| 6 | Окружность |  | Окружность через три точки . |
| 7 | Окружность |  | Окружность через три точки . |
| 8 | Отрезок |  | Отрезок . |

Рис. 25
2-й случай: пусть искомая окружность касается одной из окружностей (например, проходящей через точки ) внутренним образом, а двух других внешним образом (рис. 26).

Рис 26
Пусть – центр этой окружности, а ее радиус равен Тогда, воспользуемся теоремой: точки касания и центры касающихся окружностей лежат на одной прямой и расстояние между центрами равно сумме радиусов при внешнем касании и их разности при внутреннем.
Тогда .
Рассмотрим прямоугольный треугольник , где точка – проекция точки на диагональ
В этом треугольнике
Из теоремы Пифагора получаем
Отсюда получаем
Соответственно в данной задаче при получаем два ответа и .
Ответ: 14 или 6.
Задача 8. К двум окружностям, расположенным одна вне другой, проведены одна внешняя и одна внутренняя касательные. Рассмотрим две прямые, каждая из которых проходит через точки касания, принадлежащие одной из окружностей. Докажите, что точка пересечения этих прямых расположена на прямой, соединяющей центры окружностей.
Доказательство. Сделаем построение в GeoGebra (рис. 27) Обозначим центры окружностей через и . Внешняя касательная касается первой окружности в точке , а второй окружности в точке ; внутренняя касательная касается первой окружности в точке , а второй окружности в точке .
Пусть прямые и пересекают прямую в точках и соответственно. Надо доказать, что . Рассмотрим точки пересечения прямых и , и , исоответственно. , поэтому прямоугольные треугольники подобны, а также и . Из параллельности этих прямых получаем
Из подобия четырёхугольников получаем
Следовательно, , т. е. ч.т.д.

Рис. 27
Задача 9. (ЕГЭ, 2014 ) На гипотенузе прямоугольного треугольника опустили высоту . Из точки катеты опустили перпендикуляры и.
а) Докажите, что точки лежат на одной окружности.
б) Найдите радиус этой окружности, если .
Решение.
а) Докажем, что четырехугольник можно вписать в окружность.
Четырехугольник можно вписать в окружность, если сумма противоположных углов четырехугольника равна 180 градусов.
Шаги создания чертежа в GeoGebra (таб. 7):
Таблица 7
| № | Имя | Иконка GeoGebra | Определение |
| 1 | Окружность с диаметром |  | Окружность с радиусом . |
| 2 | Точка |  | Точка пересечения прямых и . |
| 3 | Прямая |  | Прямая через , перпендикулярная . |
| 4 | Точка |  | Точка пересечения прямых . |
| 5 | Прямая |  | Прямая через , перпендикулярная . |
| 6 | Точка |  | Точка пересечения прямых . |
| 7 | Прямая |  | Прямая через , перпендикулярная . |
| 8 | Точка |  | Точка пересечения прямых. |
| 9 | Отрезок |  | Отрезок. |
| 10 | Угол |  | Угол . |
| 11 | Угол |  | Угол . |
| 12 | Окружность |  | Окружность через три точки . |

Рис. 28
Из чертежа (рис. 28) видно, что сумма противолежащих углов в четырехугольнике равна 180 градусов, . Значит, около четырехугольника можно описать окружность. (ч.т.д.)
б) Найдите радиус этой окружности, если .
Рассмотрим прямоугольный треугольник . Угол – вписанный угол, который опирается на диаметр , и, следовательно, . В этом треугольнике мы знаем катет . По условию задачи . Найдем второй катет. Для этого рассмотрим четырехугольник :
и четырехугольник – параллелограмм:
(по условию).
Итак, задача свелась к нахождению гипотенузы прямоугольного треугольника :
, отсюда .
Ответ: 6,5.
2.8. Линейные и угловые элементы треугольника
Задача 10. (ЕГЭ, 2015) Дан прямоугольный треугольник с прямым углом при вершине при вершине и углом при вершине. Точка – середина гипотенузы. Точка симметрична точке относительно прямой . Найдите угол .
Решение. Рассмотрим два случая: и .
Рассуждения, справедливые для обоих случаев:
.
Поскольку точка симметрична точке относительно прямой , то и перпендикулярна .
Значит, , , треугольники и равны.
.
.
Из прямоугольного треугольника , .
, следовательно, треугольник – равнобедренный. Угол при его вершине .
А углы при основании .
Соответственные углы , следовательно, прямые параллельны. Следовательно, .
1-й случай:.
Рассмотрим решение в GeoGebra (Рис. 29). В данном случае, , тогда .

Рис. 29
2-й случай:.
Рассмотрим решение в GeoGebre (Рис. 30). В данном случае,, тогда .

Рис. 30
3-й случай: если то задача не имеет смысла, т.к. точки и совпадают.
1 2 3 4 5 6 7