Файл: Лекции по дисциплине Надежность сельскохозяйственной техники Тема 1. Введение. Цель и задачи курса. Цель Изучение теории надежности транспортной техники План.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 190
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
) (8)
Это соотношение является одним из основных уравнений теории надежности.
К числу важнейших общих зависимостей надежности относятся зависимости надежности систем от надежности элементов. Исходя из теоремы умножения вероятностей, вероятность безотказной работы системы равна произведению вероятностей безотказной работы отдельных элементов.
Обычно вероятность безотказной работы элементов достаточно высока, поэтому, пользуясь теорией приближенных вычислений, получаем:
Рст = 1- nQ(t) (9)
Пусть в системе из шести одинаковых элементов P1(t) =0,99.
Тогда Q(t) =0,01 и Рст(t) =0,94.
Вероятность безотказной работы нужно уметь определять для любого промежутка времени. По теореме умножения вероятностей
P(T+t) = P(T) P(t) или P(t) =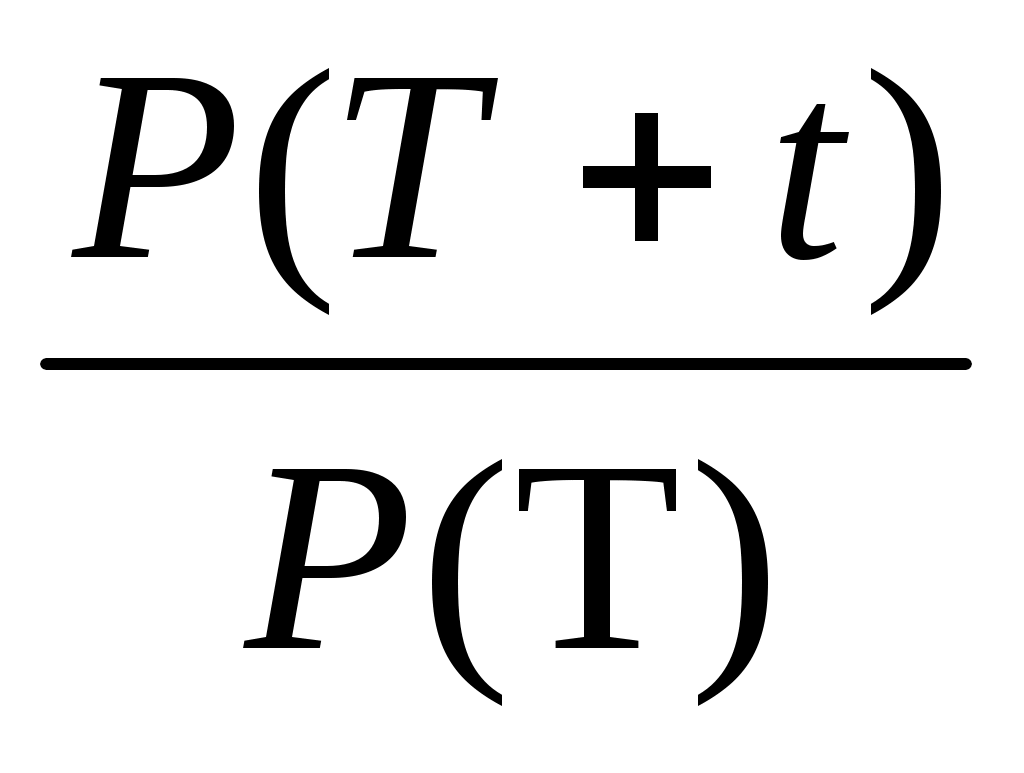
(10)
3.3 Характеристика случайности событий применительно к отказу объектов
В результате технические объекты подвергаются не только переменным, но и случайным воздействиям. Поэтому для анализа и контроля надежности используется теория вероятностей и математическая статистика.
Методы исследований надежности основаны на том, что отказ - случайное событие и для его предупреждения необходимо знать физические причины и закономерности возникновения и развития его.
В теории вероятности и основанной на ней математической статистике применяют ряд специфических понятий, основными из которых служат следующие: испытание (опыт), событие, случайная величина, вероятность, частота, частость.
Испытание (опыт) это практическое создание некоторых условий, влияющих на некоторое физическое явление.
Событие-это явление, происходящее в результате испытания (опыта).
Достоверным называют такое событие, которое неизбежно произойдет при данных условиях.
Невозможным называют событие, которое при тех же условиях произойти не может.
Случайным называют событие, которое при данных условиях может произойти, а может и не произойти.
С точки зрения количественной характеристики все явления делятся на единичные и массовые.
Единичное возникает однократно и при многократном воспроизведении того же опыта практически не повторится.
Массовыми называют явления, повторяющиеся при многократном воспроизведении испытаний.
Несовместными называют два события, если при испытании появление одного из них исключает появление другого (например: отказ и работоспособность).
Совместными называют два события, если появление одного из них не исключает появления второго.
Случайная величина – это такая величина, которая в результате опыта может принимать различные значения в определенных пределах.
Частота - это число одинаковых или близких появлений события или абсолютных значений случайных величин, соединенных в одну группу(интервал) или разряд.
Частость или относительная частота - это частота , выраженная в долях единицы или в процентах от общего числа испытаний или объектов изучаемой совокупности.
При проведении большого числа испытаний обнаруживают определенные закономерности в наступлении случайных событий. Изучение этих закономерностей составляет одну из задач теории вероятности.
Вероятность – это объективная математическая оценка возможности реализации случайного события или случайной величины.
Вероятность события А – это отношение числа случаев, благоприятствующих наступлению данного события, ко всему числу событий. Приближенное равенство P ≈ m/N позволяет определить вероятность Р какого-либо события по эмпирической частости.
Вероятность события принято выражать положительным числом, имеющим значения от нуля до единицы, т.е. 0 ≤ Р (А) ≤ 1. Если m = N, то Р(А)=m/N=1 и событие А достоверно(обязательно произойдет); при Р(А)=0 событие невозможно (произойти не может).
3.4. Формулы теории вероятности. Формулы сложения и умножения вероятностей
Вероятности случайных событий можно складывать или умножать.
Формула сложения вероятностей. Если при испытании может произойти только одно из событий, а вместе они произойти не могут, то они называются несовместными. Это сложное событие событие А называют суммой исходных событий и условно обозначают :
А = А1+ А2 + + Аn =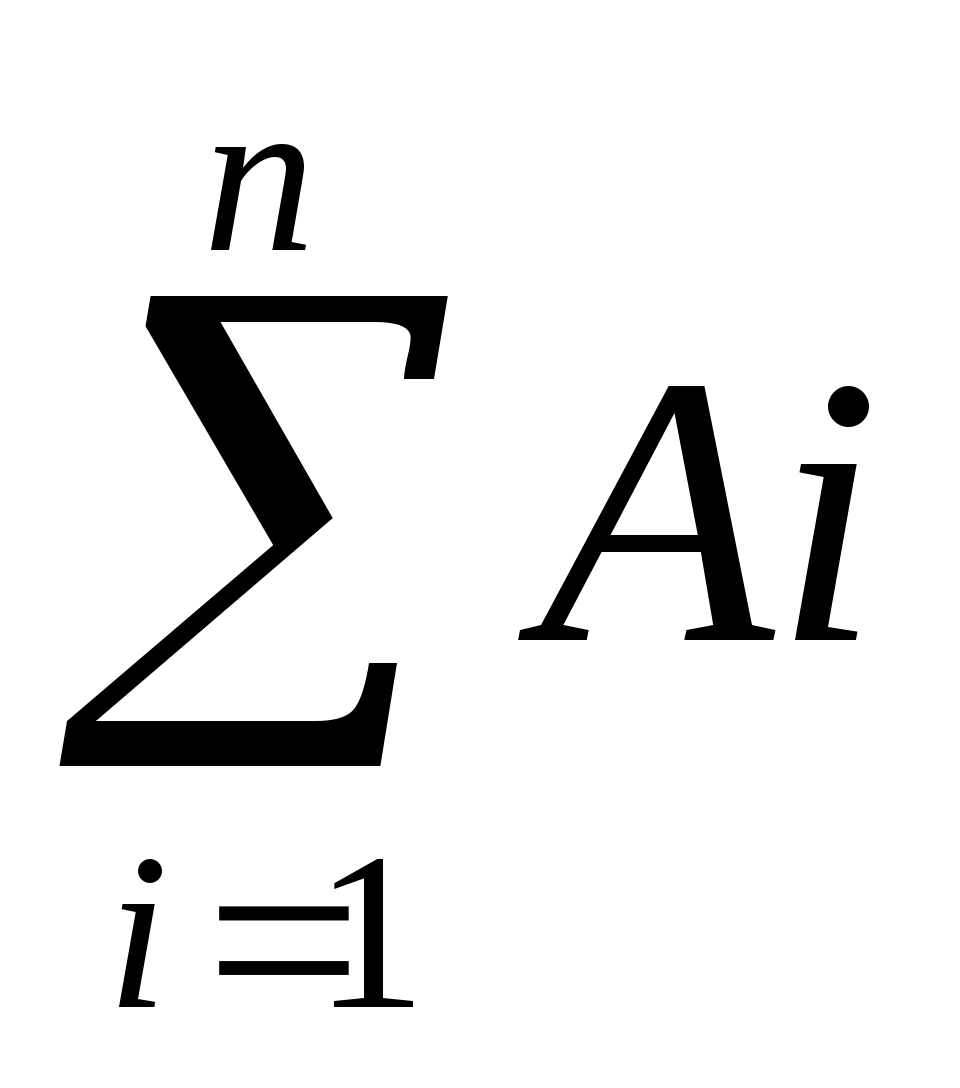
(11)
Если вероятности подчиняются таким же соотношениям, что и соответствующие им частоты, то получают формулу (теорему) сложения вероятностей, применяемую для несовместных событий.
Вероятность появления одного из нескольких независимых и несовместных однородных (принадлежащих к одной группе событий)событий (или иначе вероятность суммы несовместных событий А
1 , А2 , ,Аn) равна сумме вероятностей этих событий:
P(A) = P(A1 +A2 + + An )=P(A1) + P(A2) + P(A) + P(An) =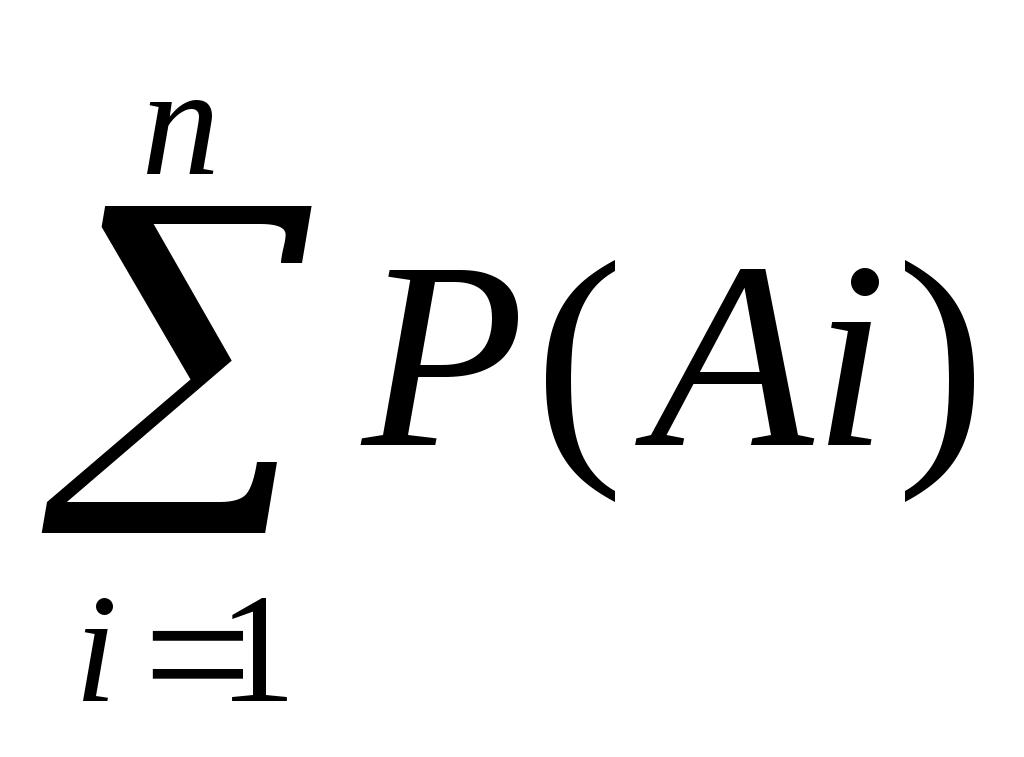
(12)
В общем случае для полной группы несовместных событий
P(A) =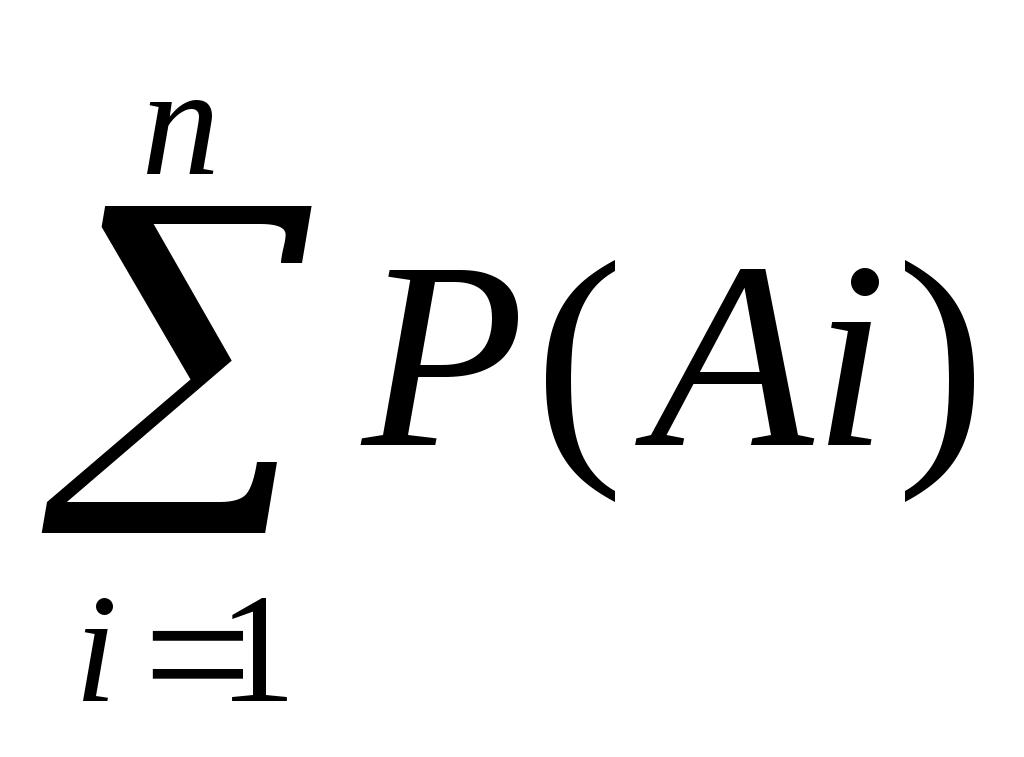 =1 (13)
Полная группа событий будет в том случае, если в результате испытаний наступит хотя бы одно из них (например, при длительных испытаниях обязательно появится отказ объекта). Для двух несовместных или противоположных событий А и
, образующих полную группу событий,
Р(А) = 1-Р( ) (14)
На практике в надежности такими событиями являются состояние работоспособности объекта и отказ. Эти события образуют полную группу, для которой P + q = 1 (15)
где Р- вероятность того, что объект будет работоспособным;
q – вероятность того, что наступит отказ.
Т.к. события противоположны, т.е. появление одного из них достоверно, а совместное появление обоих сразу в одном опыте невозможно, то
q = 1 – Р (16)
Для двух совместных событий Р(А1+А2)=Р(А1)+Р(А2)–Р(А1,А2) (17)
Формула умножения вероятностей. Если два события А и В независимы, т.е. появление одного из них не изменяет вероятности появления другого, то Р(АВ) = Р(А) Р(В), (18)
т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
При Р(А) = Р(В) Р(А В) = Р(А)2.
Сложное событие А , заключающееся в одновременном осуществлении нескольких событий, называется произведением исходных событий Аi и условно обозначается А = А1 А2 А3 , Аn =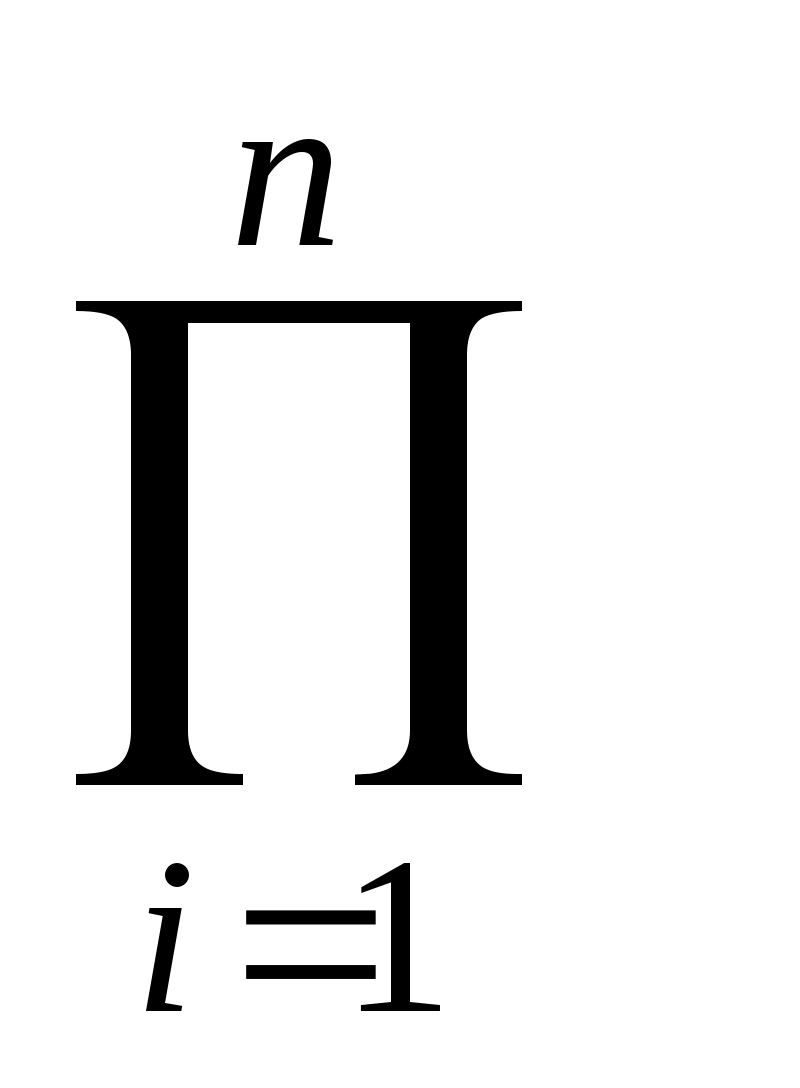
Р(Аi) (19)
По теореме умножения вероятностей независимых событий
Р(А) = Р(А1 А2 ,Аn) =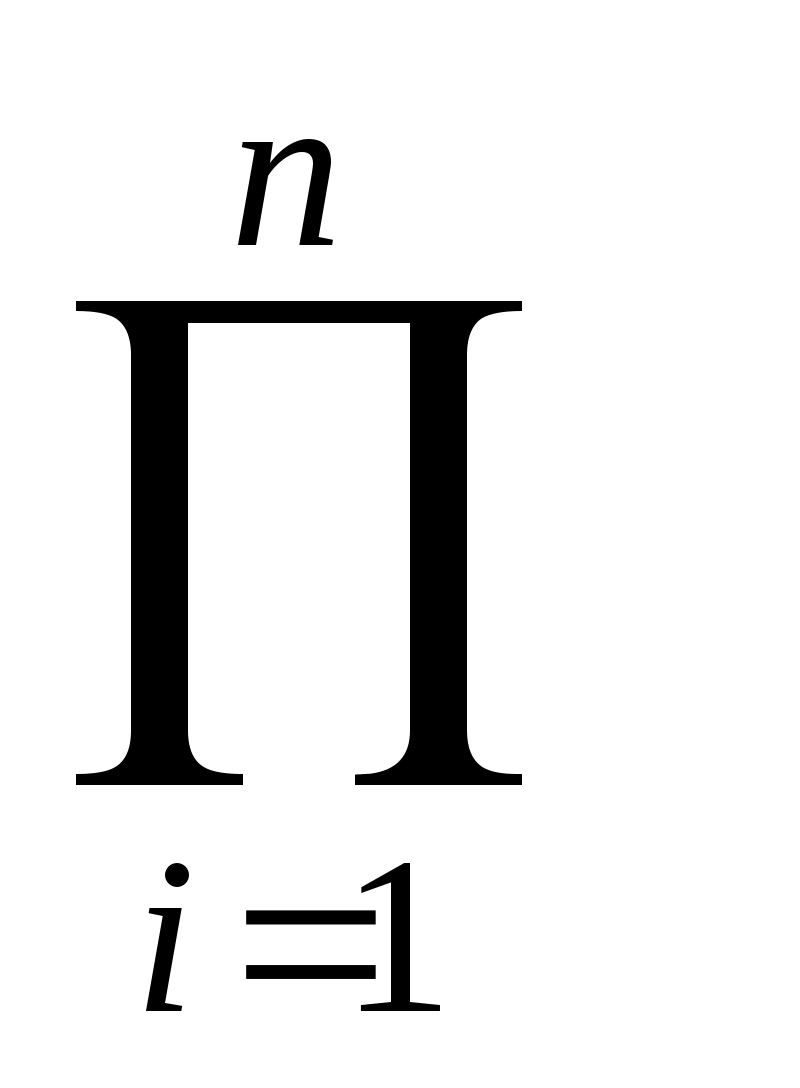 Р(Аi), (20)
если Р(А1) =Р(А2) = Р(А) =Р, то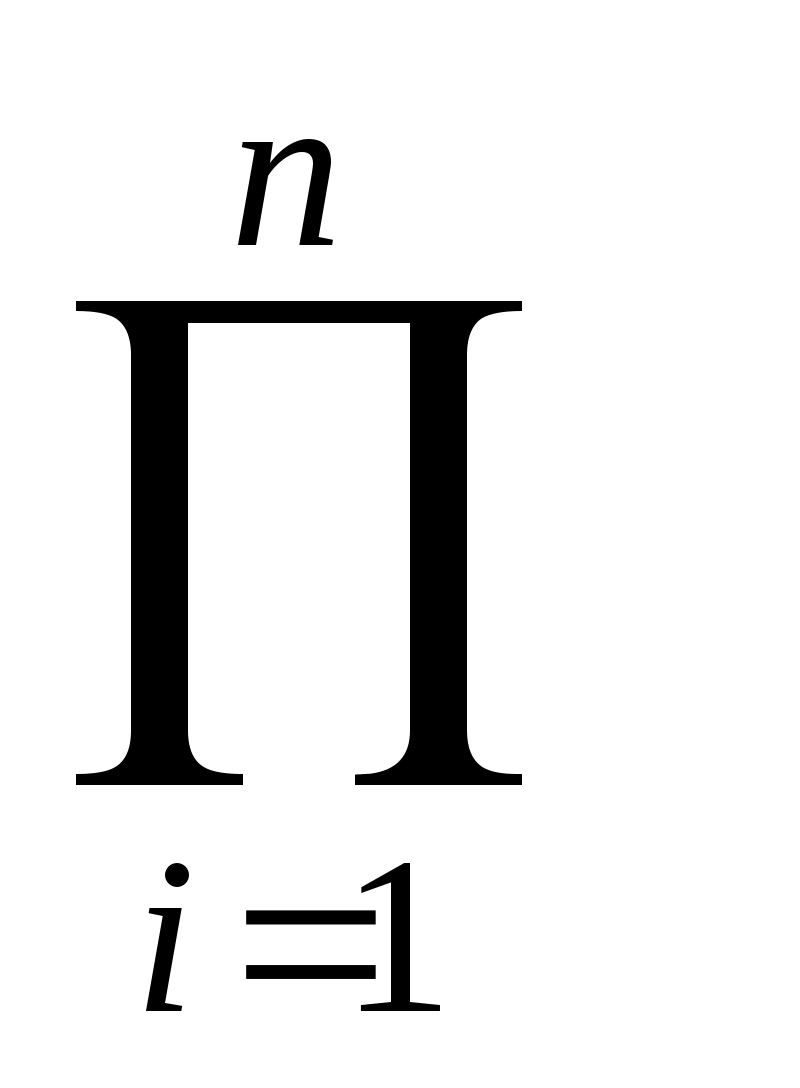
Р(Аi) Рn (21)
Для достаточно больших значений P, обозначая через q вероятность противоположного события (Р = 1-q )
Р(А) = (1- q )n (22)
Если события несовместны, то произведение таких событий является невозможным событием, вероятность которого равна нулю. Основные характеристики надежности имеют значительный разброс, т.е. они случайные величины, а поэтому при многократном повторении они подчиняются определенным статистически устойчивым законам распределения случайной величины.
Список рекомендуемой литературы
1.Ермолов Л.С., Кряжков В.М., Черкун В.Е., - Основы надежности сельскохозяйственной техники. М.: Колос, 1982
2.Ю.Н. Артемьев Качество ремонта и надежность машин в сельском хозяйстве. М, Колос, 1981
3.Д.Н.Решетов, А.С. Иванов, В.З. Фадеев Надежность машины М, Высшая школа, 1988.
4.В.И. Прейсман. Основы надежности сельскохозяйственной техники. Киев-Донецк «Вица школа», 1979.
Контрольные вопросы:
1. Как записывается формула плотности распределения случайной величины?
2. Что такое математическое ожидание, дисперсия, коэффициент вариации случайной величины?
3. Как определяется вероятность безотказной работы и интенсивность отказов?
4. Что такое случайная величина, частота, частость, вероятность события А?
5. В каких случаях применяется формула сложения случайных событий и в каких формула умножения вероятностей?
Тема № 5,6. Случайные величины и распределение вероятностей. Числовые характеристики распределения вероятностей.
Цель: Изучение основных понятий теории надежности технологических машин.
План:
1. Место теории вероятности и математической статистики в теории надежности машин.
2. Распределение случайных величин. Закон распределения случайной величины.
3. Характеристики распределения случайной величины.
4. Статистическая оценка надежности. Законы распределения, характеризующие надежность.
5. Критерии согласия.
6. Доверительная вероятность оценки точности определения математического ожидания и дисперсии.
5.1. Необходимые сведения из теории вероятностей и математической статистики.
При работе сельскохозяйственные машины подвергаются воздействию самых различных процессов. Все эти факторы реально существуют и являются объективными. Кроме того, работа машин зависит от субъективности факторов, тоже реально существующих, но связанных с человеком.
Перечисленные факторы столь многообразны, что машины одной марки, одного типа будут отличаться по своим характеристикам. Наработку любой машины до отказа или до предельного состояния заранее предугадать нельзя. Любой отказ в работе из-за большого числа действующих факторов следует рассматривать как событие случайное.
Закономерности в случайных событиях изучает специальный раздел математики – теория вероятностей. С учетом случайности отказов при работе машин изучение ряда вопросов в теории вероятности строится на основе положения теории вероятностей.
Основной характеристикой случайного события является – вероятность. Принято считать, что вероятность достоверного события (такого, которое обязательно произойдет), равна 1. Вероятность же невозможного события (которое в тех же условиях произойти заведомо не может) равна 0. Таким образом, вероятность любого случайного события – есть положительная величина лежащая от 0 до 1.
Кроме понятия случайного события в теории вероятности установлено понятие случайной величины, т.е. такая величина, которая в результате опыта может принимать различные значения в определенных пределах. Примерами случайной величины являются ресурс машины, наработка на отказ и др. Различают: непрерывные случайные величины – которые в некотором интервале могут принимать любые значения (величина износа, любой технический параметр машины) и дискретные – которые могут принимать лишь определенные значения (число негодных деталей в партии).
Поскольку для установления вероятности какого-либо события необходимо провести бесконечно большое число опытов, то на практике используют раздел теории вероятности – мат. статистику, и вероятность случайного события оценивается статистической вероятностью. Если из N опытов интересующее событие произошло m раз, то статистическая вероятность (частость) отказов W=m/N. При неограниченном увеличении N статистическое значение частости W приближается к некоторому числу Р, называемому вероятностью данного события:
Р = limW=lim m/N, т.е. P(A) m/N, (23)
где P(A) – вероятность события А; m – число случаев;
N – число несовместных, возможных и равнозначных событий.
Это соотношение является одним из основных уравнений теории надежности.
К числу важнейших общих зависимостей надежности относятся зависимости надежности систем от надежности элементов. Исходя из теоремы умножения вероятностей, вероятность безотказной работы системы равна произведению вероятностей безотказной работы отдельных элементов.
Обычно вероятность безотказной работы элементов достаточно высока, поэтому, пользуясь теорией приближенных вычислений, получаем:
Рст = 1- nQ(t) (9)
Пусть в системе из шести одинаковых элементов P1(t) =0,99.
Тогда Q(t) =0,01 и Рст(t) =0,94.
Вероятность безотказной работы нужно уметь определять для любого промежутка времени. По теореме умножения вероятностей
P(T+t) = P(T) P(t) или P(t) =
(10)3.3 Характеристика случайности событий применительно к отказу объектов
В результате технические объекты подвергаются не только переменным, но и случайным воздействиям. Поэтому для анализа и контроля надежности используется теория вероятностей и математическая статистика.
Методы исследований надежности основаны на том, что отказ - случайное событие и для его предупреждения необходимо знать физические причины и закономерности возникновения и развития его.
В теории вероятности и основанной на ней математической статистике применяют ряд специфических понятий, основными из которых служат следующие: испытание (опыт), событие, случайная величина, вероятность, частота, частость.
Испытание (опыт) это практическое создание некоторых условий, влияющих на некоторое физическое явление.
Событие-это явление, происходящее в результате испытания (опыта).
Достоверным называют такое событие, которое неизбежно произойдет при данных условиях.
Невозможным называют событие, которое при тех же условиях произойти не может.
Случайным называют событие, которое при данных условиях может произойти, а может и не произойти.
С точки зрения количественной характеристики все явления делятся на единичные и массовые.
Единичное возникает однократно и при многократном воспроизведении того же опыта практически не повторится.
Массовыми называют явления, повторяющиеся при многократном воспроизведении испытаний.
Несовместными называют два события, если при испытании появление одного из них исключает появление другого (например: отказ и работоспособность).
Совместными называют два события, если появление одного из них не исключает появления второго.
Случайная величина – это такая величина, которая в результате опыта может принимать различные значения в определенных пределах.
Частота - это число одинаковых или близких появлений события или абсолютных значений случайных величин, соединенных в одну группу(интервал) или разряд.
Частость или относительная частота - это частота , выраженная в долях единицы или в процентах от общего числа испытаний или объектов изучаемой совокупности.
При проведении большого числа испытаний обнаруживают определенные закономерности в наступлении случайных событий. Изучение этих закономерностей составляет одну из задач теории вероятности.
Вероятность – это объективная математическая оценка возможности реализации случайного события или случайной величины.
Вероятность события А – это отношение числа случаев, благоприятствующих наступлению данного события, ко всему числу событий. Приближенное равенство P ≈ m/N позволяет определить вероятность Р какого-либо события по эмпирической частости.
Вероятность события принято выражать положительным числом, имеющим значения от нуля до единицы, т.е. 0 ≤ Р (А) ≤ 1. Если m = N, то Р(А)=m/N=1 и событие А достоверно(обязательно произойдет); при Р(А)=0 событие невозможно (произойти не может).
3.4. Формулы теории вероятности. Формулы сложения и умножения вероятностей
Вероятности случайных событий можно складывать или умножать.
Формула сложения вероятностей. Если при испытании может произойти только одно из событий, а вместе они произойти не могут, то они называются несовместными. Это сложное событие событие А называют суммой исходных событий и условно обозначают :
А = А1+ А2 + + Аn =
(11)Если вероятности подчиняются таким же соотношениям, что и соответствующие им частоты, то получают формулу (теорему) сложения вероятностей, применяемую для несовместных событий.
Вероятность появления одного из нескольких независимых и несовместных однородных (принадлежащих к одной группе событий)событий (или иначе вероятность суммы несовместных событий А
1 , А2 , ,Аn) равна сумме вероятностей этих событий:
P(A) = P(A1 +A2 + + An )=P(A1) + P(A2) + P(A) + P(An) =
(12)В общем случае для полной группы несовместных событий
P(A) =
=1 (13)Полная группа событий будет в том случае, если в результате испытаний наступит хотя бы одно из них (например, при длительных испытаниях обязательно появится отказ объекта). Для двух несовместных или противоположных событий А и
, образующих полную группу событий, Р(А) = 1-Р(
) (14)На практике в надежности такими событиями являются состояние работоспособности объекта и отказ. Эти события образуют полную группу, для которой P + q = 1 (15)
где Р- вероятность того, что объект будет работоспособным;
q – вероятность того, что наступит отказ.
Т.к. события противоположны, т.е. появление одного из них достоверно, а совместное появление обоих сразу в одном опыте невозможно, то
q = 1 – Р (16)
Для двух совместных событий Р(А1+А2)=Р(А1)+Р(А2)–Р(А1,А2) (17)
Формула умножения вероятностей. Если два события А и В независимы, т.е. появление одного из них не изменяет вероятности появления другого, то Р(АВ) = Р(А) Р(В), (18)
т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
При Р(А) = Р(В) Р(А В) = Р(А)2.
Сложное событие А , заключающееся в одновременном осуществлении нескольких событий, называется произведением исходных событий Аi и условно обозначается А = А1 А2 А3 , Аn =
Р(Аi) (19)По теореме умножения вероятностей независимых событий
Р(А) = Р(А1 А2 ,Аn) =
Р(Аi), (20)если Р(А1) =Р(А2) = Р(А) =Р, то
Р(Аi) Рn (21)
Для достаточно больших значений P, обозначая через q вероятность противоположного события (Р = 1-q )
Р(А) = (1- q )n (22)
Если события несовместны, то произведение таких событий является невозможным событием, вероятность которого равна нулю. Основные характеристики надежности имеют значительный разброс, т.е. они случайные величины, а поэтому при многократном повторении они подчиняются определенным статистически устойчивым законам распределения случайной величины.
Список рекомендуемой литературы
1.Ермолов Л.С., Кряжков В.М., Черкун В.Е., - Основы надежности сельскохозяйственной техники. М.: Колос, 1982
2.Ю.Н. Артемьев Качество ремонта и надежность машин в сельском хозяйстве. М, Колос, 1981
3.Д.Н.Решетов, А.С. Иванов, В.З. Фадеев Надежность машины М, Высшая школа, 1988.
4.В.И. Прейсман. Основы надежности сельскохозяйственной техники. Киев-Донецк «Вица школа», 1979.
Контрольные вопросы:
1. Как записывается формула плотности распределения случайной величины?
2. Что такое математическое ожидание, дисперсия, коэффициент вариации случайной величины?
3. Как определяется вероятность безотказной работы и интенсивность отказов?
4. Что такое случайная величина, частота, частость, вероятность события А?
5. В каких случаях применяется формула сложения случайных событий и в каких формула умножения вероятностей?
Тема № 5,6. Случайные величины и распределение вероятностей. Числовые характеристики распределения вероятностей.
Цель: Изучение основных понятий теории надежности технологических машин.
План:
1. Место теории вероятности и математической статистики в теории надежности машин.
2. Распределение случайных величин. Закон распределения случайной величины.
3. Характеристики распределения случайной величины.
4. Статистическая оценка надежности. Законы распределения, характеризующие надежность.
5. Критерии согласия.
6. Доверительная вероятность оценки точности определения математического ожидания и дисперсии.
5.1. Необходимые сведения из теории вероятностей и математической статистики.
При работе сельскохозяйственные машины подвергаются воздействию самых различных процессов. Все эти факторы реально существуют и являются объективными. Кроме того, работа машин зависит от субъективности факторов, тоже реально существующих, но связанных с человеком.
Перечисленные факторы столь многообразны, что машины одной марки, одного типа будут отличаться по своим характеристикам. Наработку любой машины до отказа или до предельного состояния заранее предугадать нельзя. Любой отказ в работе из-за большого числа действующих факторов следует рассматривать как событие случайное.
Закономерности в случайных событиях изучает специальный раздел математики – теория вероятностей. С учетом случайности отказов при работе машин изучение ряда вопросов в теории вероятности строится на основе положения теории вероятностей.
Основной характеристикой случайного события является – вероятность. Принято считать, что вероятность достоверного события (такого, которое обязательно произойдет), равна 1. Вероятность же невозможного события (которое в тех же условиях произойти заведомо не может) равна 0. Таким образом, вероятность любого случайного события – есть положительная величина лежащая от 0 до 1.
Кроме понятия случайного события в теории вероятности установлено понятие случайной величины, т.е. такая величина, которая в результате опыта может принимать различные значения в определенных пределах. Примерами случайной величины являются ресурс машины, наработка на отказ и др. Различают: непрерывные случайные величины – которые в некотором интервале могут принимать любые значения (величина износа, любой технический параметр машины) и дискретные – которые могут принимать лишь определенные значения (число негодных деталей в партии).
Поскольку для установления вероятности какого-либо события необходимо провести бесконечно большое число опытов, то на практике используют раздел теории вероятности – мат. статистику, и вероятность случайного события оценивается статистической вероятностью. Если из N опытов интересующее событие произошло m раз, то статистическая вероятность (частость) отказов W=m/N. При неограниченном увеличении N статистическое значение частости W приближается к некоторому числу Р, называемому вероятностью данного события:
Р = limW=lim m/N, т.е. P(A) m/N, (23)
где P(A) – вероятность события А; m – число случаев;
N – число несовместных, возможных и равнозначных событий.