Файл: Лекции по дисциплине Надежность сельскохозяйственной техники Тема 1. Введение. Цель и задачи курса. Цель Изучение теории надежности транспортной техники План.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 194
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
i , соответствующее наибольшей ординате полигона распределения (рисунок 4а). За моду прерывной случайной величины принимают значение, имеющее наибольшую вероятность.
5) Мода М00 теоретического распределения случайной величины – это такое значение xi, которое соответствует максимальному значению плотности распределения f(x) (рисунок 4б).
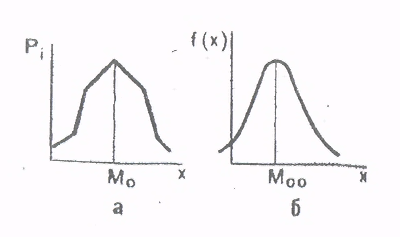
Рисунок 4. Мода случайных величин:
а – дискретной (прерывной); б - непрерывной
6) Медиана Мео теоретического распределения – это такое значение xi, при котором вероятность больших или меньших его значений одинакова, т.е. это ордината кривой распределения, которая делит площадь под ней на две равные части (рисунок 5).
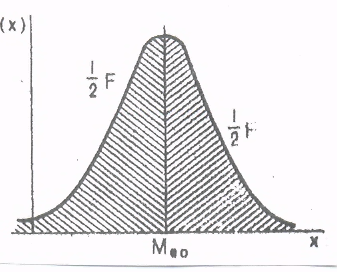
Рисунок 5. Медиана непрерывной случайной величины
Разброс случайной величины относительно центра распределения (среднеарифметической, математического ожидания, моды или медианы) характеризуется мерами рассеивания.
К мерам рассеивания относятся: размах, дисперсия (рассеивание), среднее квадратическое отклонение (стандарт) и коэффициент вариации.
7) Эмпирическое среднее квадратическое отклонение и среднее квадратическое отклонение (стандарт) будут соответственно равны корням квадратным из дисперсии S2 и из DX, взятых с положительным знаком.
При малом числе наблюдений, т.е.при N < 25
S =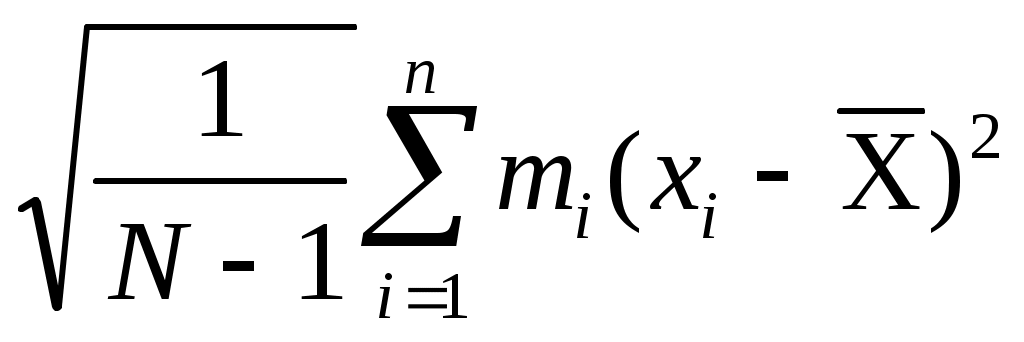
(38)
При N > 25
S =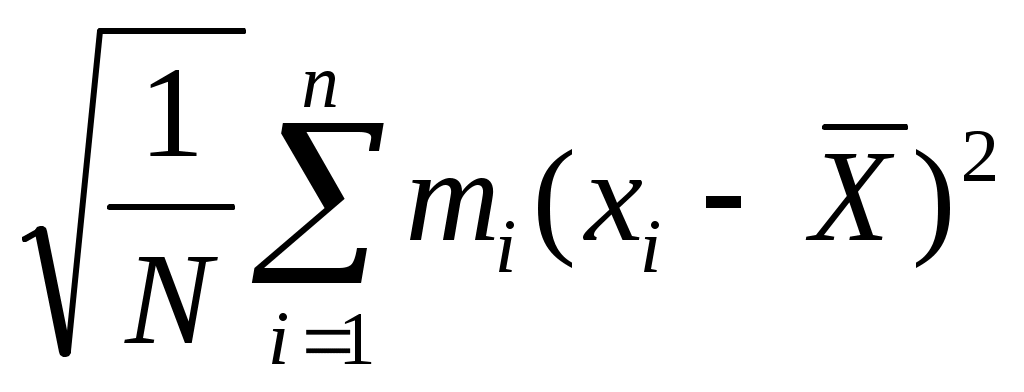
(39)
Размерности S и σ совпадают с размерностью самой случайной величины х. Если при вычислениях исходят не из отклонений от среднего арифметического, а из непосредственно измеренных величин, то
S =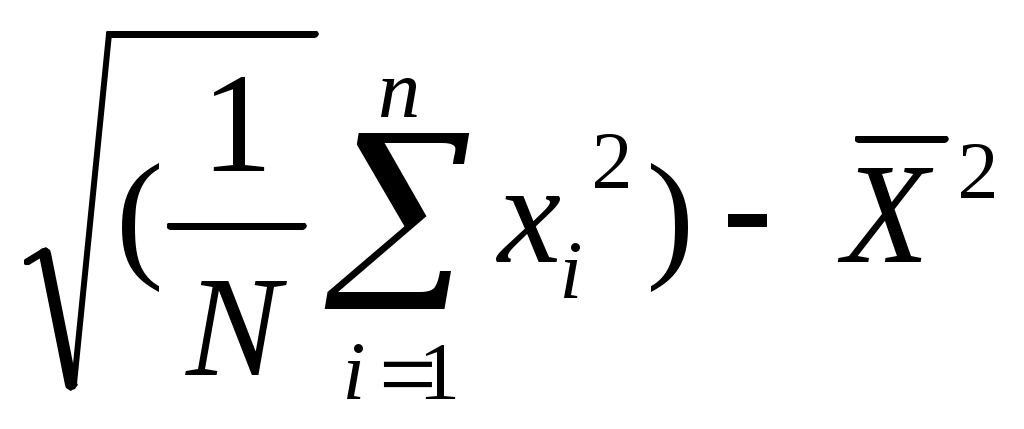
(40)
σ =
и определяет ширину кривой распределения.
Дисперсия суммы (разности) взаимно независимых случайных величин равна сумме (разности) их дисперсий.
σ2 =σ 12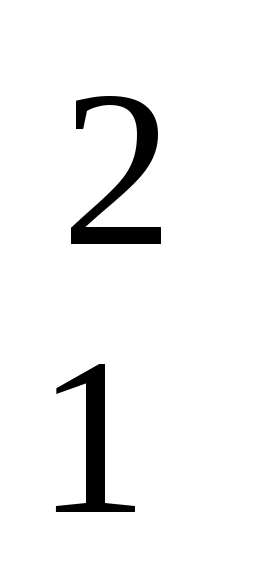 + σ
+ + σ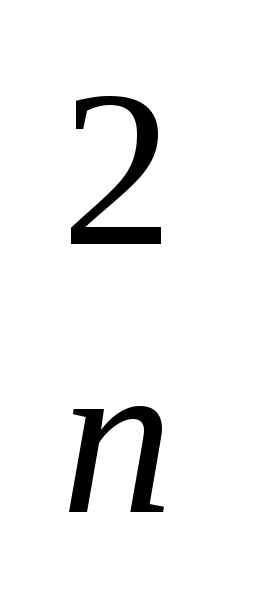
= 
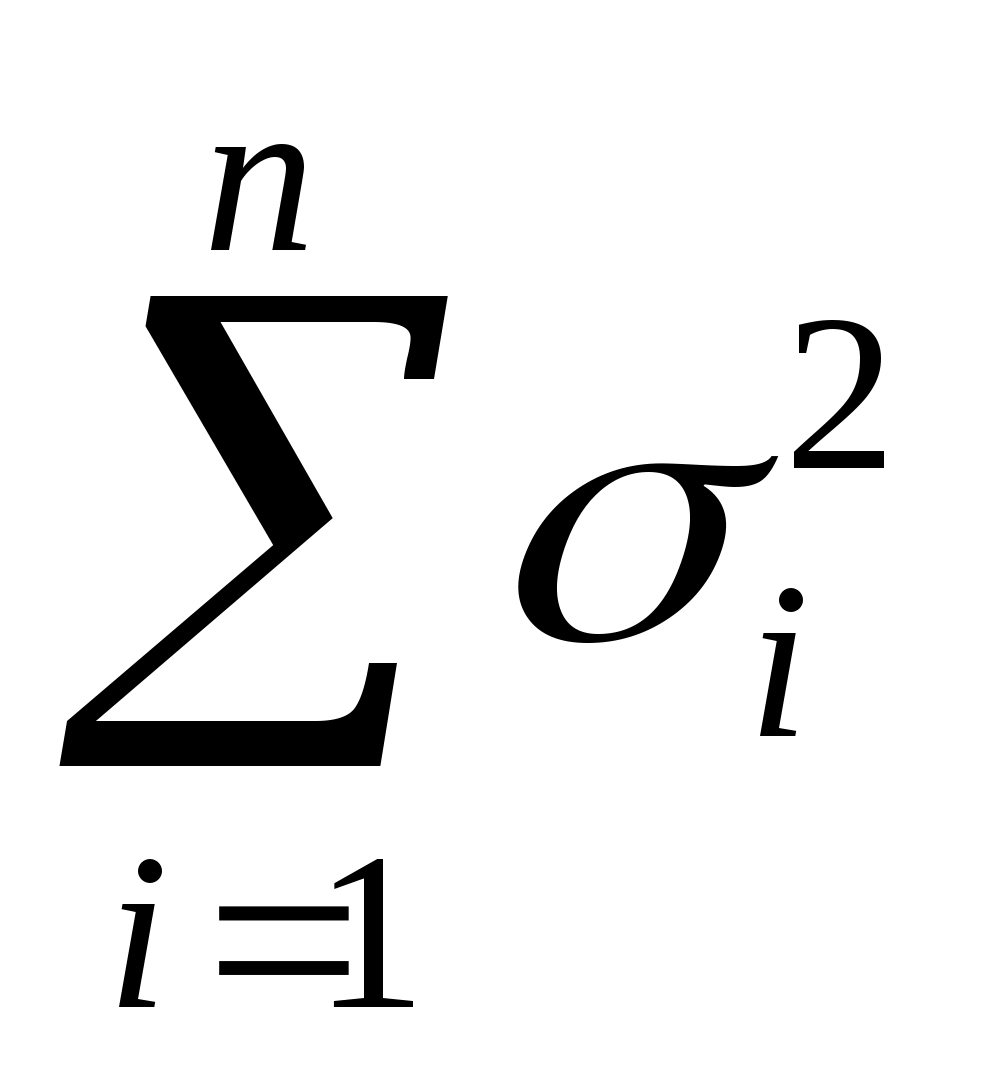
(41)
Среднее квадратическое отклонение суммы конечного числа взаимно независимых величин равно корню квадратному из суммы квадратов средних квадратических отклонений этих величин.
Среднее квадратическое отклонение величины среднего арифметического значения
(cредняя ошибка) составляет 1/N от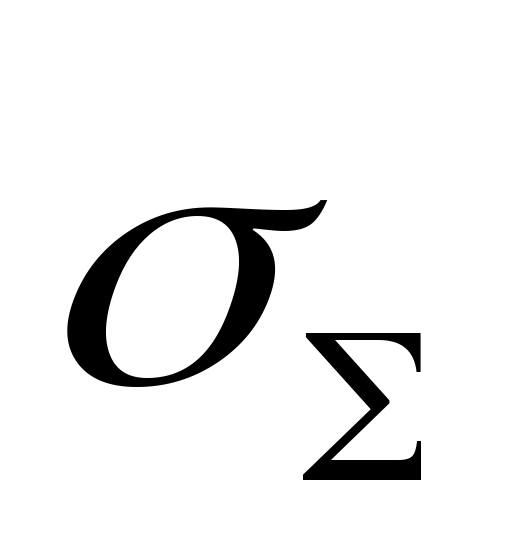 
и вычисляется как: σ X=
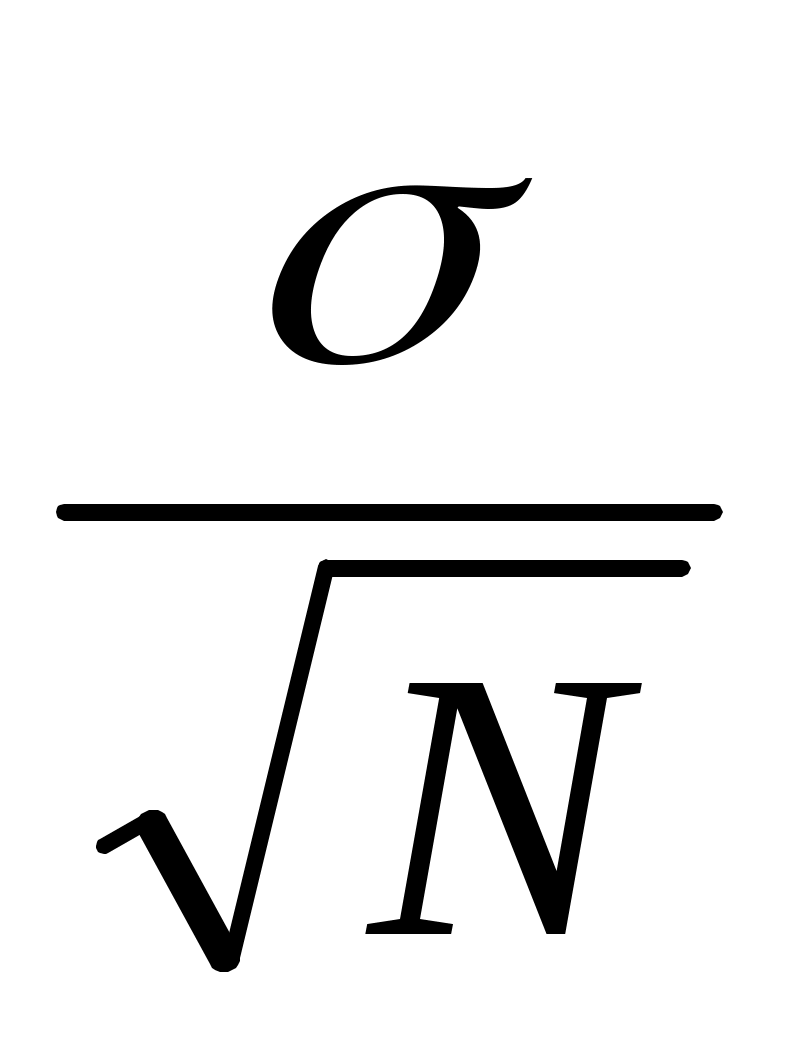(42)
Cовокупность не содержит грубых погрешностей согласно критерию Райта в том случае, если | xi | ≤ 3σ (43)
где | xi | - максимальное по абсолютной величине отклонение, равное |xmax - |.
При обработке результатов испытаний может возникнуть необходимость сравнить различные распределения, а также рассеивание разнородных величин. В качестве отвлеченной меры рассеивания, не зависящей от единиц измерения сравниваемых величин, принимается коэффициент вариации или изменчивости νx.
8) Для сравнения рассеивания разнородных величин дисперсия и стандарт не могут быть использованы. Для этого применяется коэффициент вариации υx.
Для эмпирического распределения υx=S/X – он показывает насколько велико рассеивание по сравнению со средним значением случайной величины.
Для теоретического распределения υx=/МХ (МХ – математическое ожидание).
Коэффициент вариации может быть выражен в процентах: υx=S/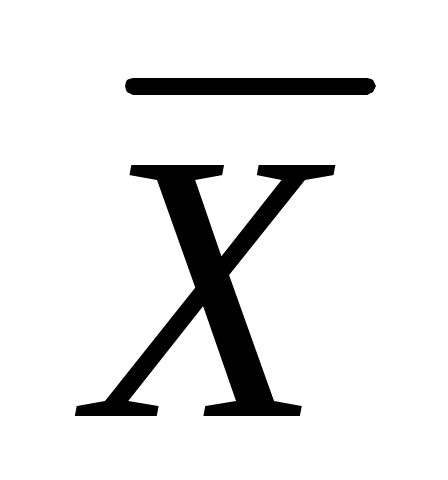
100%.
5.4 Статистическая оценка надежности. Законы распределения случайной величины, характеризующие надежность.
Сбор, обработка и анализ информации о надежности связаны с необходимостью исследования случайных событий.
Статистическая совокупность – это такая совокупность, которая состоит из однородных объектов, обладающих качественной общностью.
Генеральная или общая совокупность –
это совокупность объектов, содержащая все исследуемые объекты.
Выборка или выборочная совокупность – определенное число объектов, отобранных из исследуемой совокупности для получения сведений о генеральной совокупности.
Выборка должна быть представительной, т.е. такой, чтобы каждый объект был отобран случайно и все они имели одинаковую вероятность попасть в выборку
Объем выборки – число объектов наблюдений, составляющих выборку.
Чаще всего встречаются со следующими распределениями (законами распределения): нормальным и его разновидностями (усеченным нормальным, логарифмически нормальным); экспоненциальным (показательным); Релея; Вейбулла – Гнеденко; гамма-распределением; Пуассона; биноминальным.
Закон нормального распределенияполучил наибольшее распространение в технических приложениях(нормальный закон Гаусса). Он играет важную роль в теории вероятности и теории надежности. Этому закону подчиняются многие случайные величины массовых явлений, на которые оказывает большое число факторов, равнозначных по своим значениям (напр. износы, измерения большого числа деталей микрометрическими методами).
Плотность нормального распределения непрерывной случайной величины выглядит так: f(x) =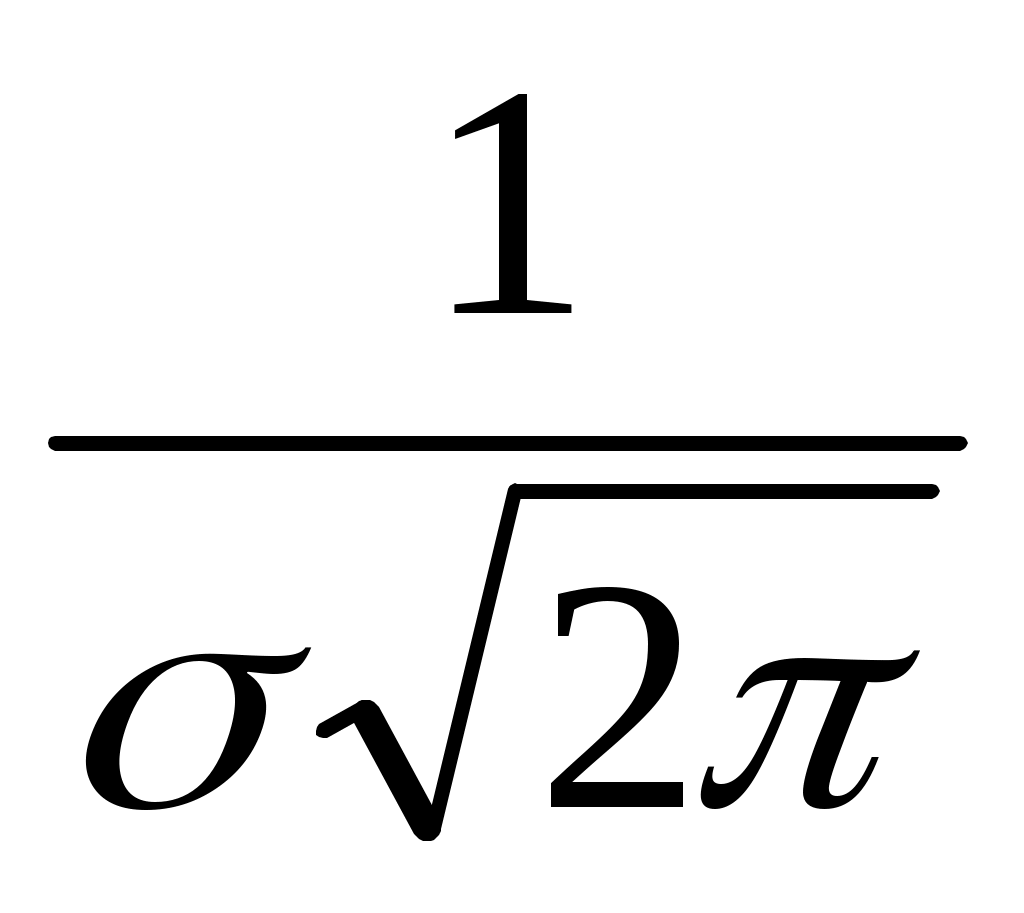
exp(-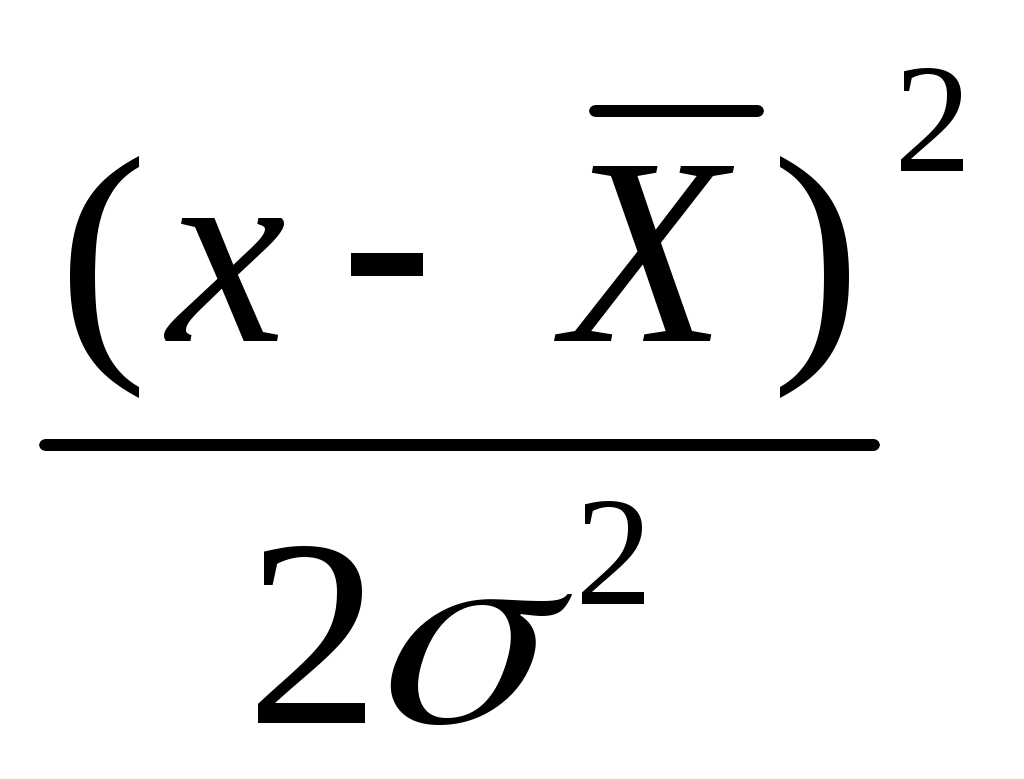
), (44)
где среднее квадратическое отклонение случайной величины х ;
е – основание натурального логарифма, равное 2,7183;
х - случайная величина (- ∞< х < +∞);
- среднее арифметическое значение(математическое ожидание) случайной величины х.
Дифференциальная кривая, соответствующая ЗНР, симметрична относительно ординаты в точке х = , называемой центром распределения, и имеет колоколообразный вид (рисунок 6).
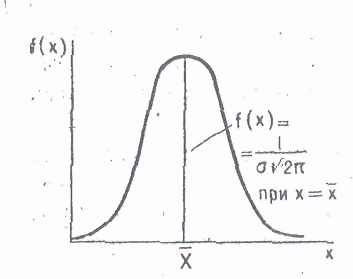
Рисунок 6. Нормальный закон распределения случайных величин.
Случайная величина, подчиняющаяся закону нормального распределения, имеет три следующих свойства; одинаковые положительные и отрицательные отклонения от средней арифметической равновозможны
; меньшие отклонения более вероятные, чем большие; весьма большие отклонения от маловероятны. Для подсчета вероятности того, что случайная величина находится в тех или иных пределах, пользуются интегралом Ф(t), значения которого приводятся в таблицах, имеющихся в литературе по математической статистике.
Интегральная функция закона нормального распределения записывается следующим образом:
F(x) =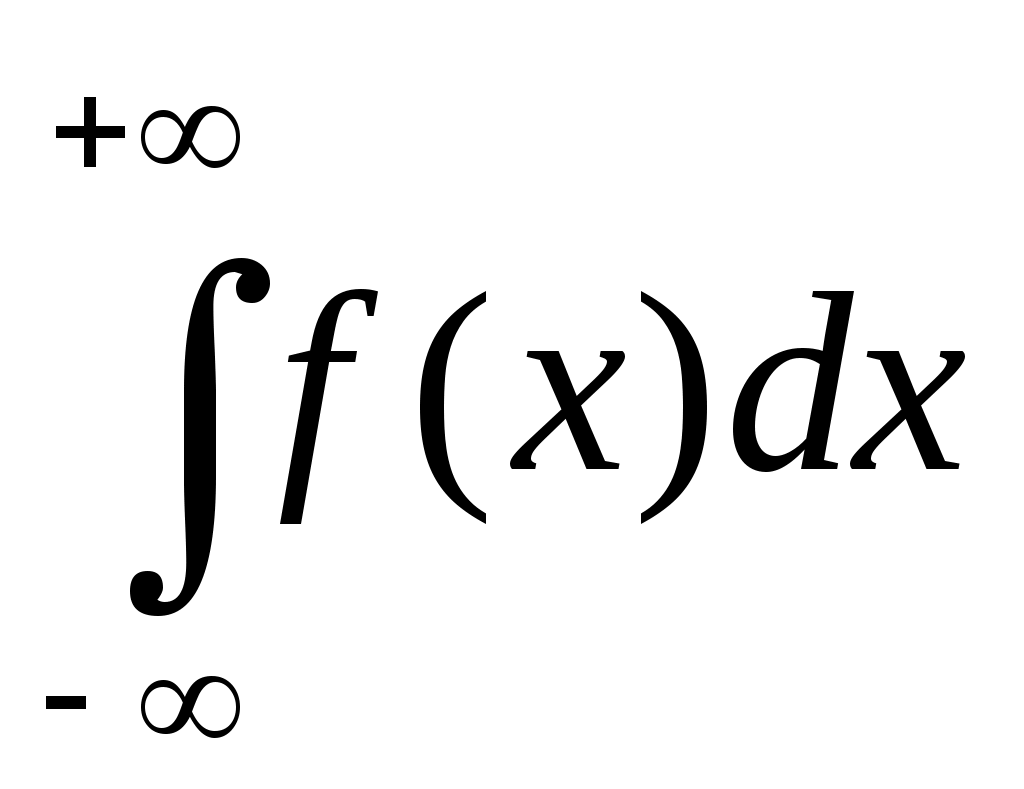
= 
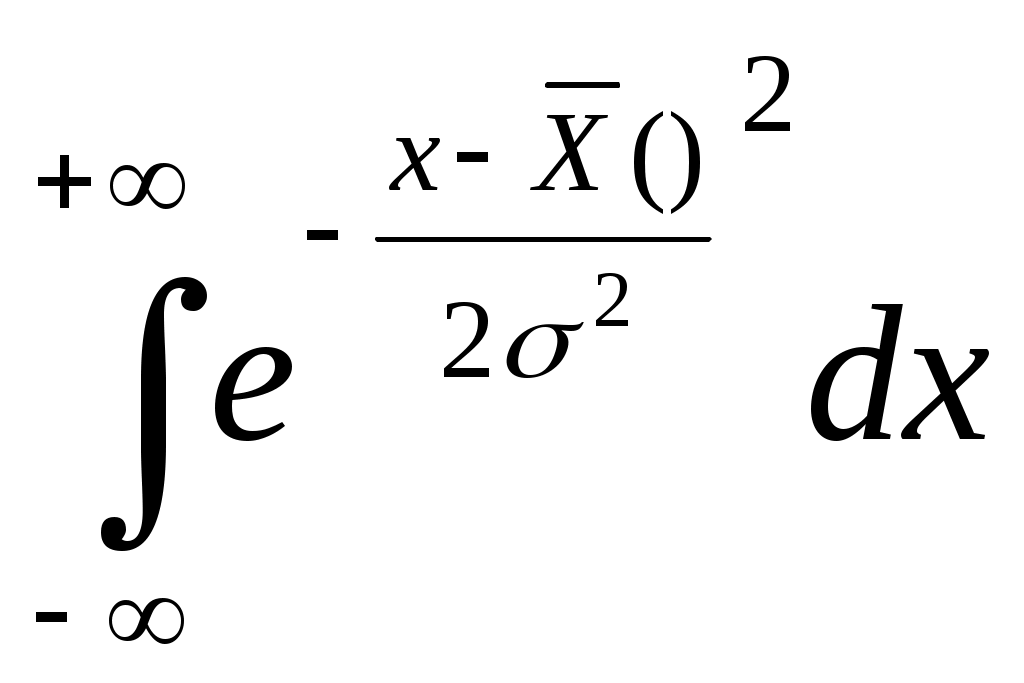(45)
Для подсчета того, что случайная величина находится в тех или иных пределах, пользуются интегралом Ф(t), значения которого приводятся в таблицах, имеющихся в литературе по математической статистике и учебниках по надежности машин.
Табличный интеграл Ф(t) соответствует площади под кривой, заключенной между осью симметрии кривой и ординатой, соответствующей значению t, и непосредственно дает вероятность того, что значение случайной величины находится в пределах от 0 до t.
Так, например, для х = 3 (t = 3) из таблиц находим Ф(t) = 0,49865, т.е. для 2Ф(3) = 0,9973 ≈ 1.Таким образом, характерной особенностью нормального распределения является то, что вероятность или частость значений х , заключенных в пределах от -3σ до +3σ, составляет 0,9973б, то есть близка к единице.
Кривые распределения, подчиняющиеся ЗНР, могут характеризоваться также асимметрией А (рисунок 7а) и эксцессом Е (рисунок 7б).
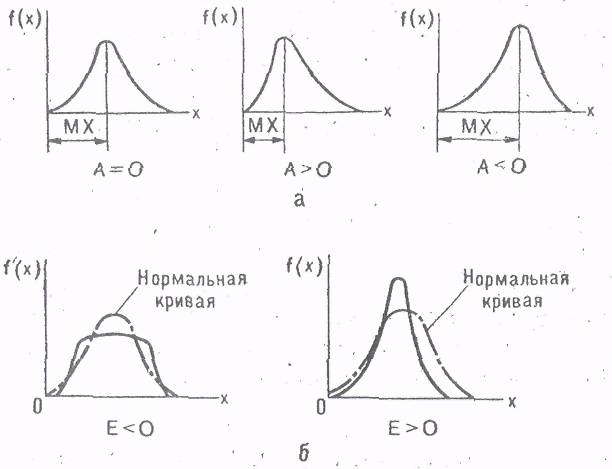
Рисунок 7. Кривые распределения (а – с асимметрией; б – с эксцессом)
При А = 0, кривая симметрична; при А>0 кривая имеет положительную асимметрию; при А<0 – отрицательную.
Эксцесс характеризует крутизну кривой. При Е<0 наблюдается отрицательный эксцесс; при Е>0 – положительный при Е=0 эксцесс отсуствует (нормальная кривая).
Для закона усеченного нормального распределения – случайная величина х с двух сторон ограничена определенными значениями.
Логарифмическое нормальное распределение – это когда десятичный логарифм случайной величины х распределяется по нормальному закону.
Экспоненциальное распределение (показательное).
Дифференциальная функция экспоненциального закона распределения случайных величин (рисунок 8а) при x ≥ 1 имеет вид:
f(x) = λe-λx = λ exp ( λx ) (46)
где λ - постоянная величина (коэффициент).
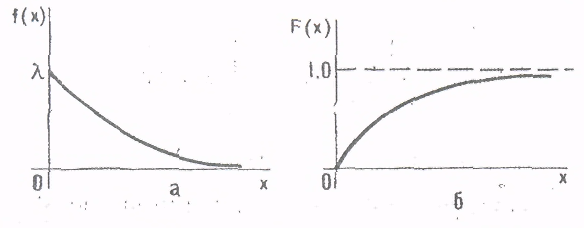
Рисунок 8. Экспоненциальный закон распределения случайных величин:
а – плотность распределения; б – функция распределения.
Интегральная функция (рисунок 8б)
F(x) =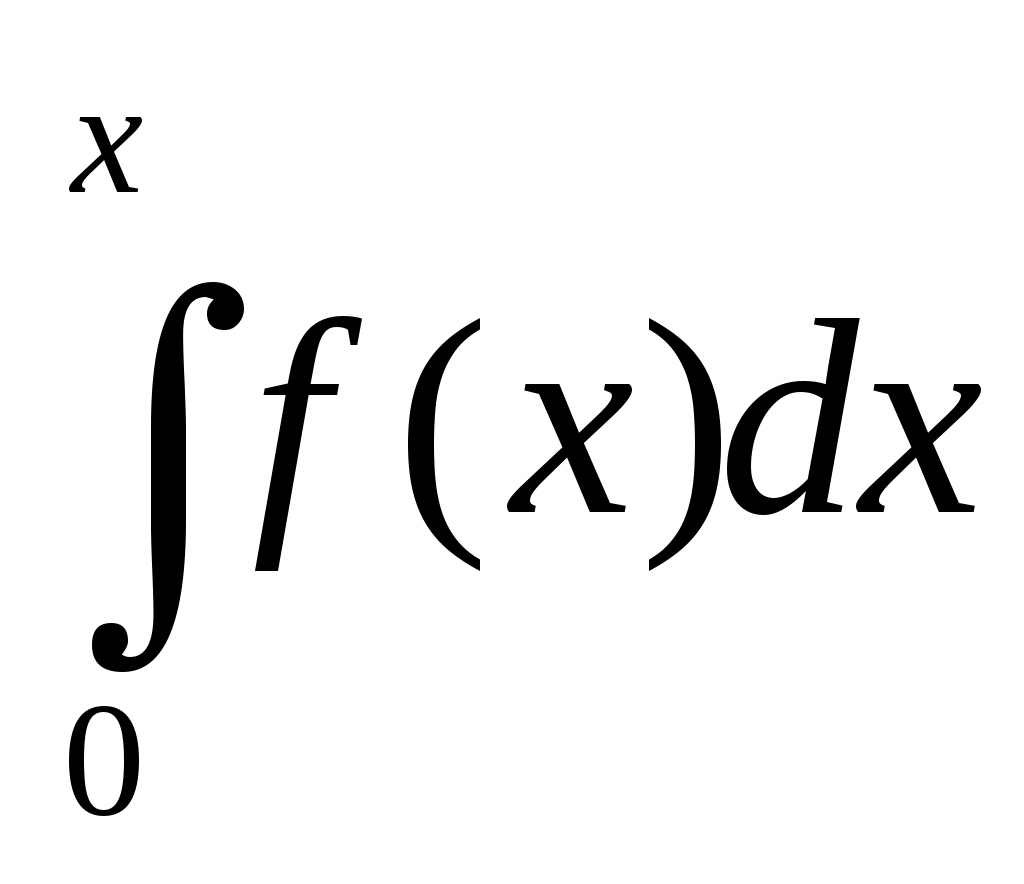
= 
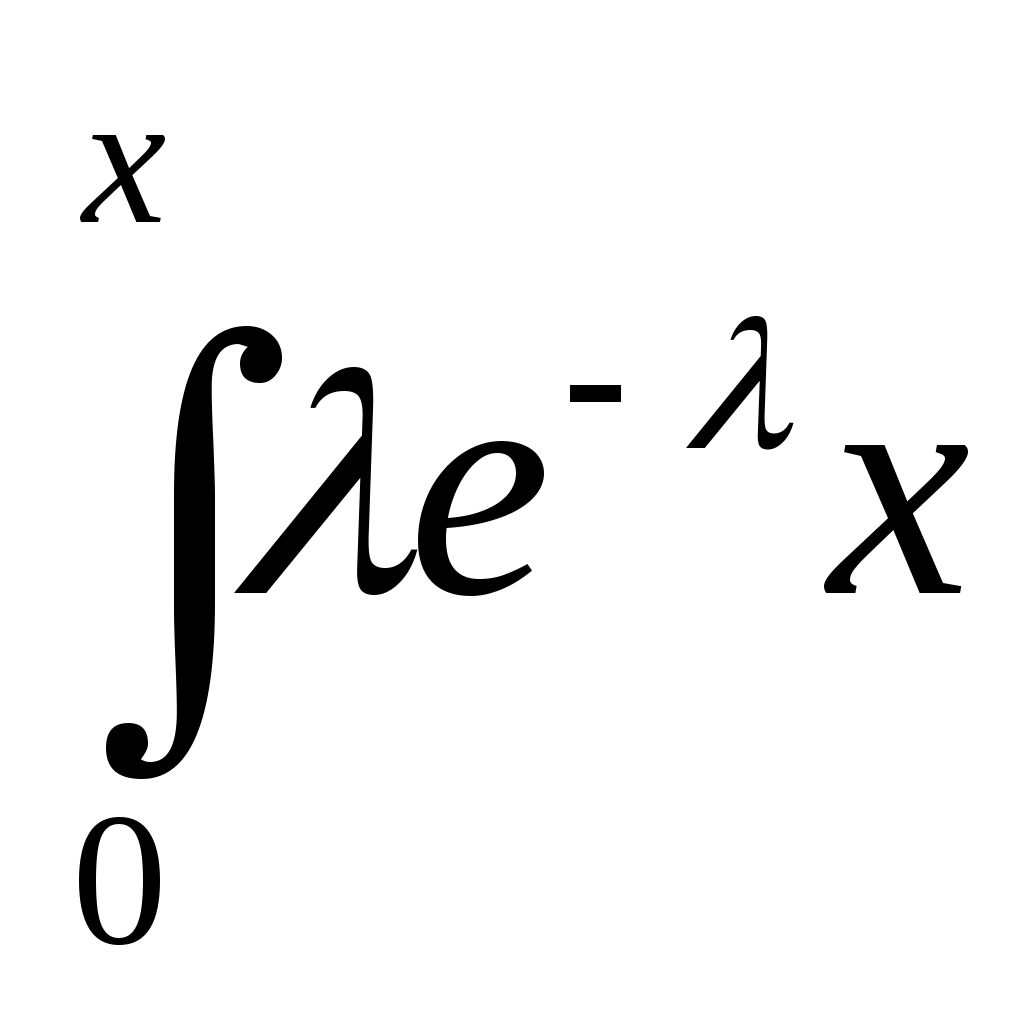= 1 – e-λx = 1 – exp(-λ x) (47)
Математическое ожидание случайной величины х, имеющей показательное распределение, - это величина, обратная коэффициенту λ.
У показательного распределения математическое ожидание и среднеквадратичное отклонение равны.
Распределение Релея - распределение положительной случайной величины происходит с плотностью распределения вида:
f(x) =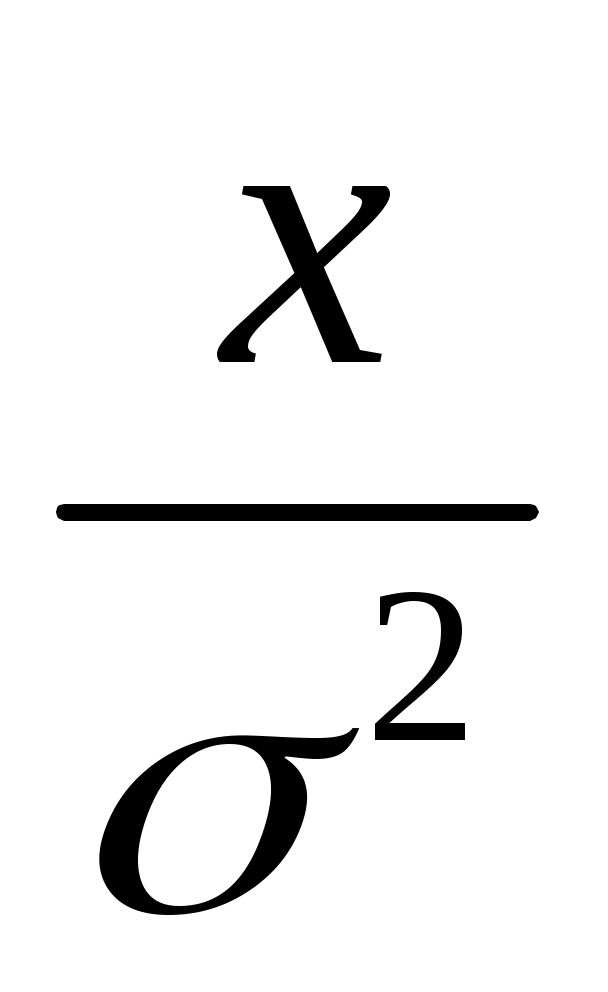
exp (-
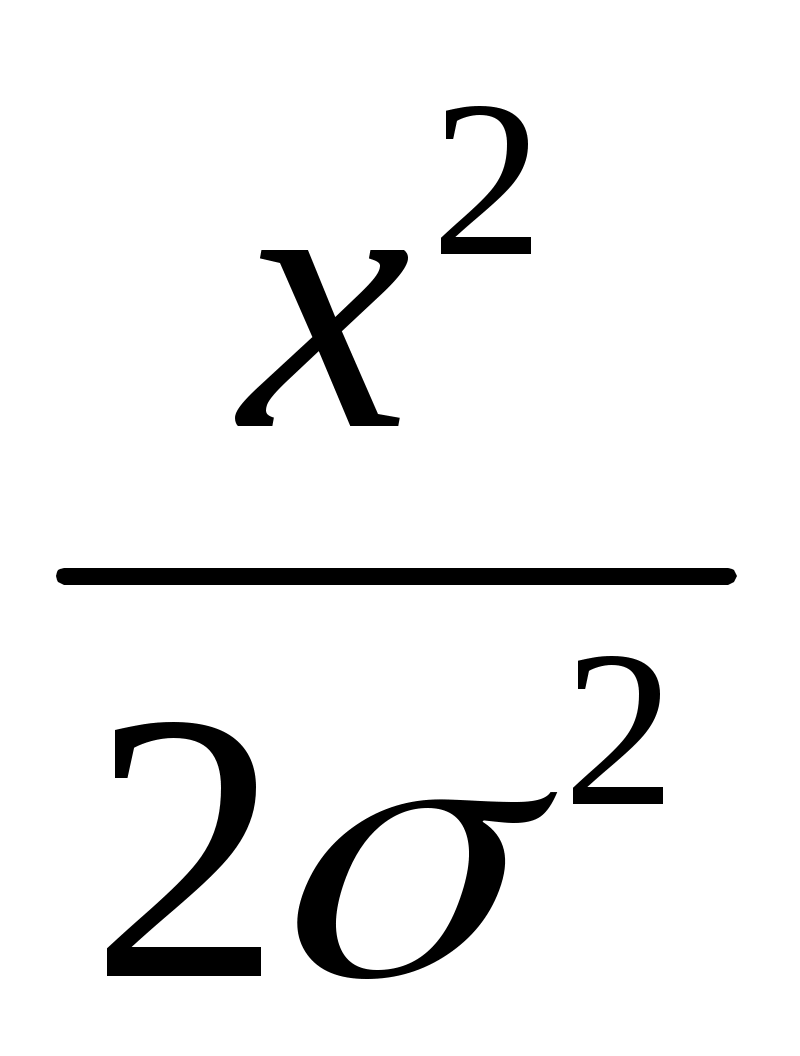) (48)
Функцию распределения Релея находят по уравнению:
F(x) =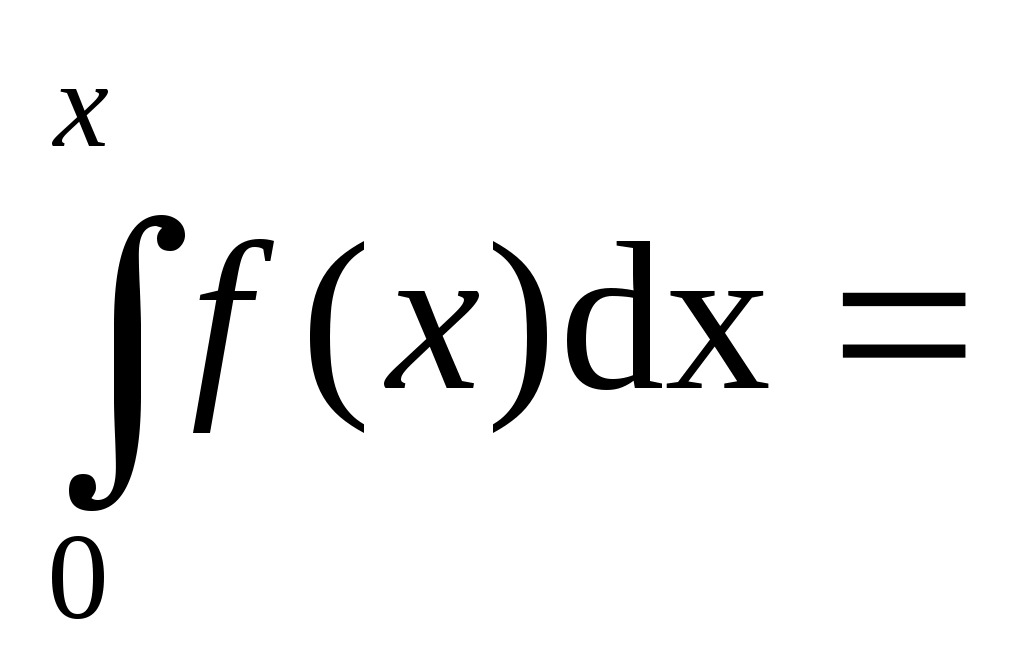
1 – exp(-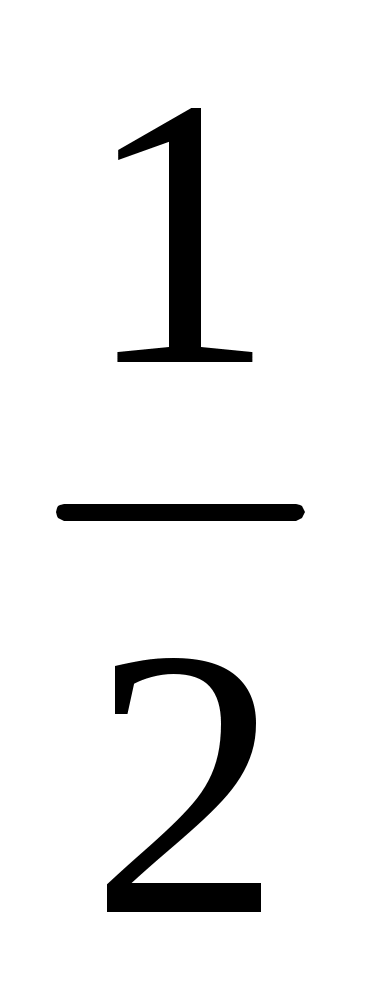 
) (49)
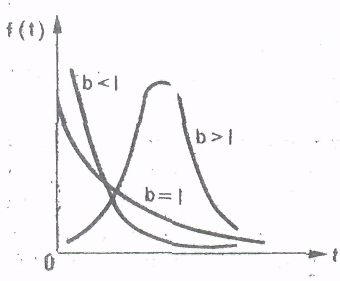
Рисунок 9. Распределение Вейбулла-Гнеденко
Распределение Вейбулла-Гнеденко (рисунок 9)имеет следующую плотность распределения:
f(x) =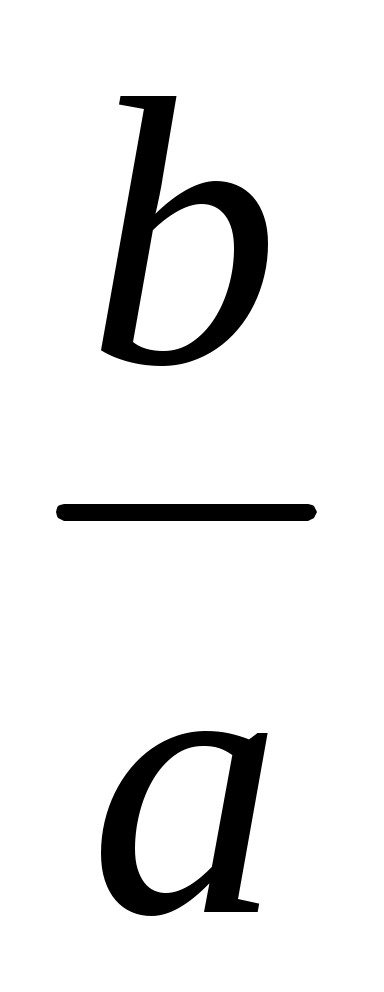
(
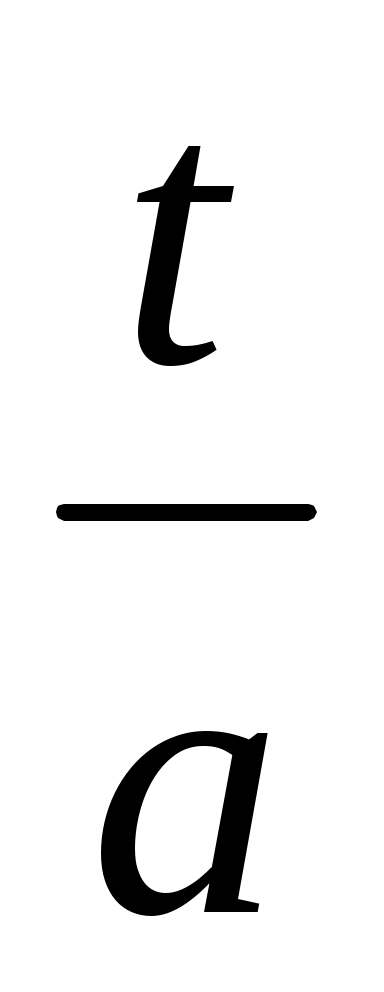)b-1 exp (- 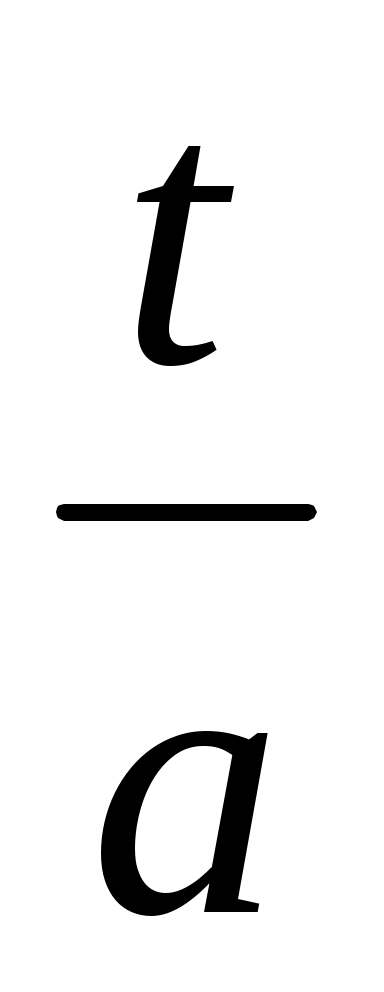)b (50)
где b и a - параметры распределения.
При b = 1 распределение Вейбулла-Гнеденко совпадает с экспоненциальным распределением, а при b = 2 – с распределением Релея.
Интегральная функция распределения: F(t) = 1 – exp [ - (
5) Мода М00 теоретического распределения случайной величины – это такое значение xi, которое соответствует максимальному значению плотности распределения f(x) (рисунок 4б).
Рисунок 4. Мода случайных величин:
а – дискретной (прерывной); б - непрерывной
6) Медиана Мео теоретического распределения – это такое значение xi, при котором вероятность больших или меньших его значений одинакова, т.е. это ордината кривой распределения, которая делит площадь под ней на две равные части (рисунок 5).
Рисунок 5. Медиана непрерывной случайной величины
Разброс случайной величины относительно центра распределения (среднеарифметической, математического ожидания, моды или медианы) характеризуется мерами рассеивания.
К мерам рассеивания относятся: размах, дисперсия (рассеивание), среднее квадратическое отклонение (стандарт) и коэффициент вариации.
7) Эмпирическое среднее квадратическое отклонение и среднее квадратическое отклонение (стандарт) будут соответственно равны корням квадратным из дисперсии S2 и из DX, взятых с положительным знаком.
При малом числе наблюдений, т.е.при N < 25
S =
(38)При N > 25
S =
(39)Размерности S и σ совпадают с размерностью самой случайной величины х. Если при вычислениях исходят не из отклонений от среднего арифметического, а из непосредственно измеренных величин, то
S =
(40)σ =
и определяет ширину кривой распределения.Дисперсия суммы (разности) взаимно независимых случайных величин равна сумме (разности) их дисперсий.
σ2 =σ 12 + σ
+ + σ =
(41)
Среднее квадратическое отклонение суммы конечного числа взаимно независимых величин равно корню квадратному из суммы квадратов средних квадратических отклонений этих величин.
Среднее квадратическое отклонение величины среднего арифметического значения
(cредняя ошибка) составляет 1/N от и вычисляется как: σ X= (42)Cовокупность не содержит грубых погрешностей согласно критерию Райта в том случае, если | xi | ≤ 3σ (43)
где | xi | - максимальное по абсолютной величине отклонение, равное |xmax -
|.При обработке результатов испытаний может возникнуть необходимость сравнить различные распределения, а также рассеивание разнородных величин. В качестве отвлеченной меры рассеивания, не зависящей от единиц измерения сравниваемых величин, принимается коэффициент вариации или изменчивости νx.
8) Для сравнения рассеивания разнородных величин дисперсия и стандарт не могут быть использованы. Для этого применяется коэффициент вариации υx.
Для эмпирического распределения υx=S/X – он показывает насколько велико рассеивание по сравнению со средним значением случайной величины.
Для теоретического распределения υx=/МХ (МХ – математическое ожидание).
Коэффициент вариации может быть выражен в процентах: υx=S/
100%.5.4 Статистическая оценка надежности. Законы распределения случайной величины, характеризующие надежность.
Сбор, обработка и анализ информации о надежности связаны с необходимостью исследования случайных событий.
Статистическая совокупность – это такая совокупность, которая состоит из однородных объектов, обладающих качественной общностью.
Генеральная или общая совокупность –
это совокупность объектов, содержащая все исследуемые объекты.
Выборка или выборочная совокупность – определенное число объектов, отобранных из исследуемой совокупности для получения сведений о генеральной совокупности.
Выборка должна быть представительной, т.е. такой, чтобы каждый объект был отобран случайно и все они имели одинаковую вероятность попасть в выборку
Объем выборки – число объектов наблюдений, составляющих выборку.
Чаще всего встречаются со следующими распределениями (законами распределения): нормальным и его разновидностями (усеченным нормальным, логарифмически нормальным); экспоненциальным (показательным); Релея; Вейбулла – Гнеденко; гамма-распределением; Пуассона; биноминальным.
Закон нормального распределенияполучил наибольшее распространение в технических приложениях(нормальный закон Гаусса). Он играет важную роль в теории вероятности и теории надежности. Этому закону подчиняются многие случайные величины массовых явлений, на которые оказывает большое число факторов, равнозначных по своим значениям (напр. износы, измерения большого числа деталей микрометрическими методами).
Плотность нормального распределения непрерывной случайной величины выглядит так: f(x) =
exp(- ), (44)где среднее квадратическое отклонение случайной величины х ;
е – основание натурального логарифма, равное 2,7183;
х - случайная величина (- ∞< х < +∞);
- среднее арифметическое значение(математическое ожидание) случайной величины х.Дифференциальная кривая, соответствующая ЗНР, симметрична относительно ординаты в точке х =
, называемой центром распределения, и имеет колоколообразный вид (рисунок 6). Рисунок 6. Нормальный закон распределения случайных величин.
Случайная величина, подчиняющаяся закону нормального распределения, имеет три следующих свойства; одинаковые положительные и отрицательные отклонения от средней арифметической равновозможны
; меньшие отклонения более вероятные, чем большие; весьма большие отклонения от
маловероятны. Для подсчета вероятности того, что случайная величина находится в тех или иных пределах, пользуются интегралом Ф(t), значения которого приводятся в таблицах, имеющихся в литературе по математической статистике.Интегральная функция закона нормального распределения записывается следующим образом:
F(x) =
= (45)Для подсчета того, что случайная величина находится в тех или иных пределах, пользуются интегралом Ф(t), значения которого приводятся в таблицах, имеющихся в литературе по математической статистике и учебниках по надежности машин.
Табличный интеграл Ф(t) соответствует площади под кривой, заключенной между осью симметрии кривой и ординатой, соответствующей значению t, и непосредственно дает вероятность того, что значение случайной величины находится в пределах от 0 до t.
Так, например, для х = 3 (t = 3) из таблиц находим Ф(t) = 0,49865, т.е. для 2Ф(3) = 0,9973 ≈ 1.Таким образом, характерной особенностью нормального распределения является то, что вероятность или частость значений х , заключенных в пределах от
-3σ до +3σ, составляет 0,9973б, то есть близка к единице.Кривые распределения, подчиняющиеся ЗНР, могут характеризоваться также асимметрией А (рисунок 7а) и эксцессом Е (рисунок 7б).
Рисунок 7. Кривые распределения (а – с асимметрией; б – с эксцессом)
При А = 0, кривая симметрична; при А>0 кривая имеет положительную асимметрию; при А<0 – отрицательную.
Эксцесс характеризует крутизну кривой. При Е<0 наблюдается отрицательный эксцесс; при Е>0 – положительный при Е=0 эксцесс отсуствует (нормальная кривая).
Для закона усеченного нормального распределения – случайная величина х с двух сторон ограничена определенными значениями.
Логарифмическое нормальное распределение – это когда десятичный логарифм случайной величины х распределяется по нормальному закону.
Экспоненциальное распределение (показательное).
Дифференциальная функция экспоненциального закона распределения случайных величин (рисунок 8а) при x ≥ 1 имеет вид:
f(x) = λe-λx = λ exp ( λx ) (46)
где λ - постоянная величина (коэффициент).
Рисунок 8. Экспоненциальный закон распределения случайных величин:
а – плотность распределения; б – функция распределения.
Интегральная функция (рисунок 8б)
F(x) =
= = 1 – e-λx = 1 – exp(-λ x) (47)Математическое ожидание случайной величины х, имеющей показательное распределение, - это величина, обратная коэффициенту λ.
У показательного распределения математическое ожидание и среднеквадратичное отклонение равны.
Распределение Релея - распределение положительной случайной величины происходит с плотностью распределения вида:
f(x) =
exp (- ) (48)Функцию распределения Релея находят по уравнению:
F(x) =
1 – exp(- ) (49) Рисунок 9. Распределение Вейбулла-Гнеденко
Распределение Вейбулла-Гнеденко (рисунок 9)имеет следующую плотность распределения:
f(x) =
( )b-1 exp (- )b (50)где b и a - параметры распределения.
При b = 1 распределение Вейбулла-Гнеденко совпадает с экспоненциальным распределением, а при b = 2 – с распределением Релея.
Интегральная функция распределения: F(t) = 1 – exp [ - (