Как правило, при изучении надежности машин имеют дело с несовместимыми случайными событиями, т.е. такими, когда появление одного исключает появление других (например, отказ и работоспособность). Для таких событий в теории вероятности применят теорему сложения вероятностей.

Вероятность суммы независимых и несовместимых событий равна сумме вероятностей этих событий:

Р(А) = Р(А₁ + А₂ +…+ А_n) = P(A₀) (24)

А также теорему умножения вероятностей: Если два события А и В независимы, т.е. появление одного из них не изменяет вероятность другого, то Р(АВ) = Р(А) * Р(В) – выражает вероятность совместного появления двух независимых событий.

---

5.2. Распределение случайных величин.

Распределение случайных величин - это совокупность значений случайных величин, расположенных в возрастающем порядке, с указанием их вероятностей (для теоретических распределений) и частостей (для эмпирических распределений).

Закон распределения случайной величины – это всякое соотношение, устанавливающее связь между возможными значениями случайных величин и соответствующими этим значениям вероятностями или частостями.

Дискретные (прерывные) случайные величины Х могут принимать только ряд отдельных значений х₁, х₂,..х_n, каждому из которых соответствует некоторое значение вероятности Р₁,Р₂,…,Р_n.

Рассматривая появление любого из перечисленных значений прерывной случайной величины как события, заметим, что эти события образуют полную группу несовместных случайных событий, а следовательно, сумма вероятностей всех возможных значений прерывистой случайной величины равна единице:

Р₁ + Р₂ + + Р_n = 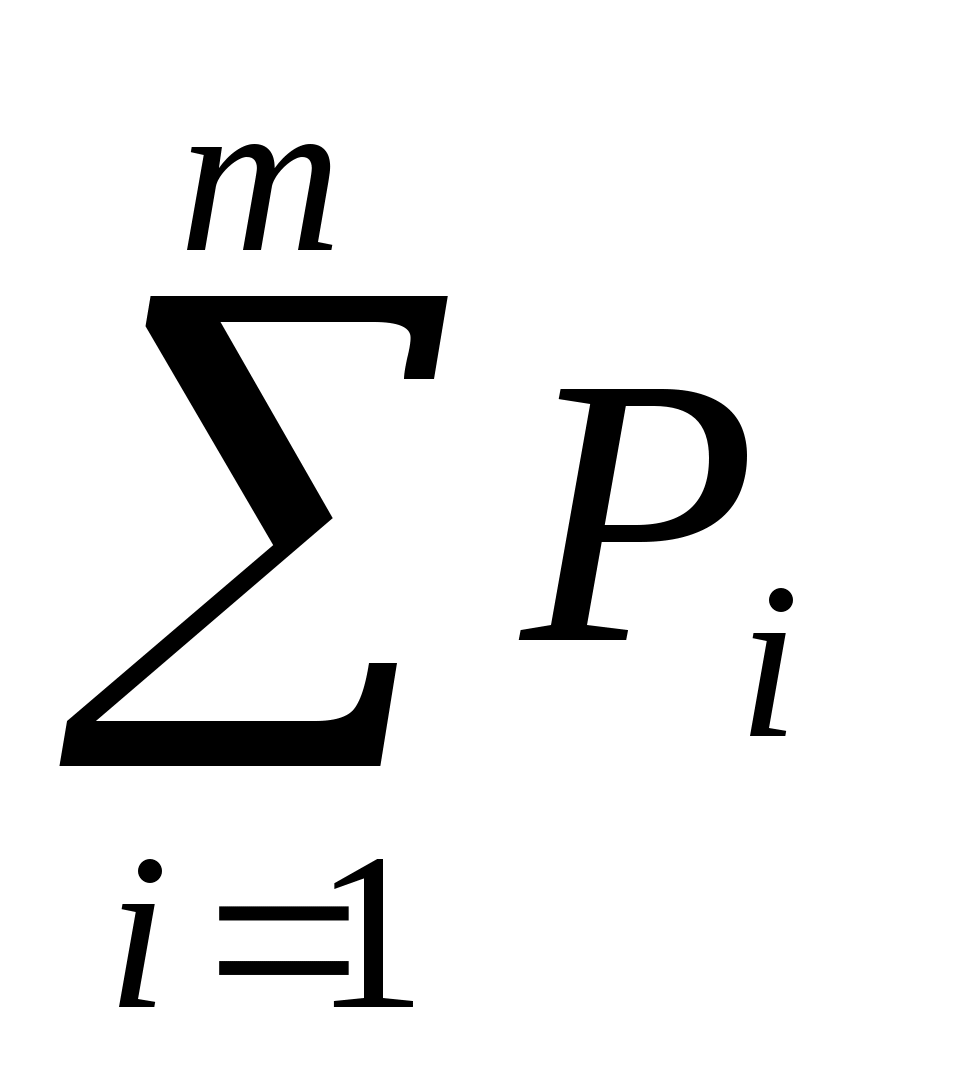= 1 (25)

Распределение прерывной случайной величины может быть представлено в виде таблицы, называемой рядом распределения (таблица 1) или графически многоугольником распределения (рисунок 1).

Таблица 1. Ряд распределения случайной величины

Значения случайной величины Х	х1	х2	…	хn
Вероятность Р (Х = хi ) = Р	Р1	Р2	…	Рn

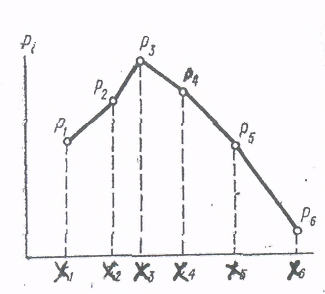
Рисунок 1.Многоугольник распределения прерывной случайной величины
При графическом представлении (см. рисунок 1) по оси абсцисс откладывают значения случайной величины х_i , а по оси ординат – вероятность Р_i, соответствующие этим значениям.

Ряд распределения и многоугольник удобны только для дискретных случайных величин. В случае непрерывной случайной величины, которая имеет бесчисленное множество значений, такая форма непригодна. В этом случае используется не вероятность события P(X=x

---

_i), а вероятность события P(Xx_i), т.е. вероятность, что случайная величина примет значение меньше какого-либо наперед выбранного значения -.

Площадь элементарного прямоугольника, равную произведению f(x)dx, называют элементом вероятности (рисунок 2). Для определения вероятности событий Р(Х < х) необходимо вычислить площадь, заключенную между кривой и осью Х в интервале от ∞ до х, т.е.сложить все элементы вероятностей в интервале от ∞ до х.

F(x) (26)


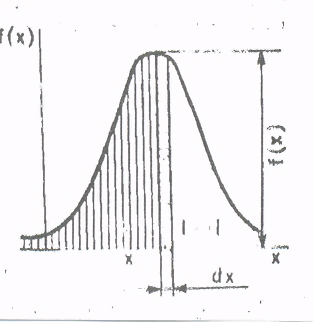
Рисунок 2. График функции f(x) для непрерывной случайной величины
Функция (интегральный закон) распределения случайной величины - наиболее универсальная характеристика как дискретных (прерывных), так и непрерывных случайных величин.

Если Х – случайная величина, а х - некоторое действительное число, то вероятность того, что Х < х:

F( x ) = P ( X < x ), (27)

где F(x) - функция распределения.

Функцию распределения можно представить в виде графика, если по оси абсцисс откладывать значение x_i , а по оси ординат – значения F(x).

Для дискретной случайной величины график функции распределения будет иметь вид ступенчатой кривой (рисунок 3).



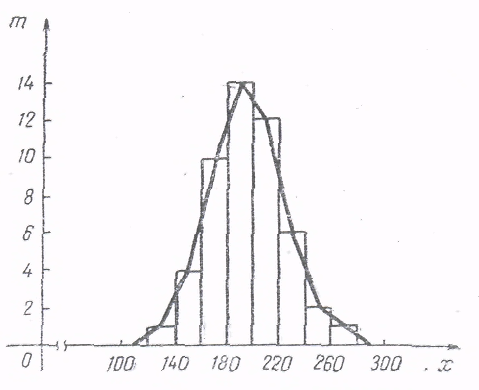
Рисунок 3. Полигон и гистограмма
Функцию распределения непрерывной случайной величины изображают плавной кривой. При любом значении х 0 < F(x) < 1.

В эмпирических распределениях возможные значения случайных величин оцениваются частотами или частостями, полученными в результате испытаний или опытов.

На практике при изучении непрерывных случайных величин их полученные значения делят на интервалы или разряды. После этого подсчитывают частоты по разрядам.

В таблице эмпирического распределения случайной величины указывают интервалы значений x_i, частоту m_i и чаcтость W_i = m_i/ N.

Эмпирическое распределение может быть изображено в виде ступенчатого графика, называемого гистограммой, или в виде ломаной линии, называемой полигоном.

О характере распределения непрерывной случайной величины в окрестностях различных точек можно судить на основании особой функции, называемой плотностью распределения.

Плотность распределения непрерывной случайной величины –

---

это производная от функции распределения непрерывной случайной величины:

f(x) = (28)

Для дискретной величины функция плотности распределения не существует.

Графически плотность распределения представляет собой кривую распределения случайных величин.

Плотность распределения характеризуется следующими основными свойствами.

1. Она неотрицательная функция от х вследствие того, что F(х) –неубывающая функция.

2. Площадь, ограниченная кривой f(x) и осью абсцисс (интеграл от плотности распределения в бесконечных пределах), равна единице, т.е.

f(x) dx = 1 (29)

При изучении случайных величин часто достаточно знать числовые характеристики распределения случайной величины.
5.3 Характеристики распределения случайной величины.

Числовые характеристики, полученные по результатам опытов, называются статистическими характеристиками случайной величины.

Теоретические характеристики, определенные по теоретическому закону распределения, называются параметрами распределения:

Основными статистическими характеристиками случайных величин, изучаемых в теории надежности, служат среднее арифметическое и среднее квадратическое отклонение.

1) Среднее арифметическое - это частное от деления суммы измеренных значений на число слагаемых этой суммы, т.е. на число испытаний (опытов).

= = (30)

Средняя взвешенная величина определяется по формуле

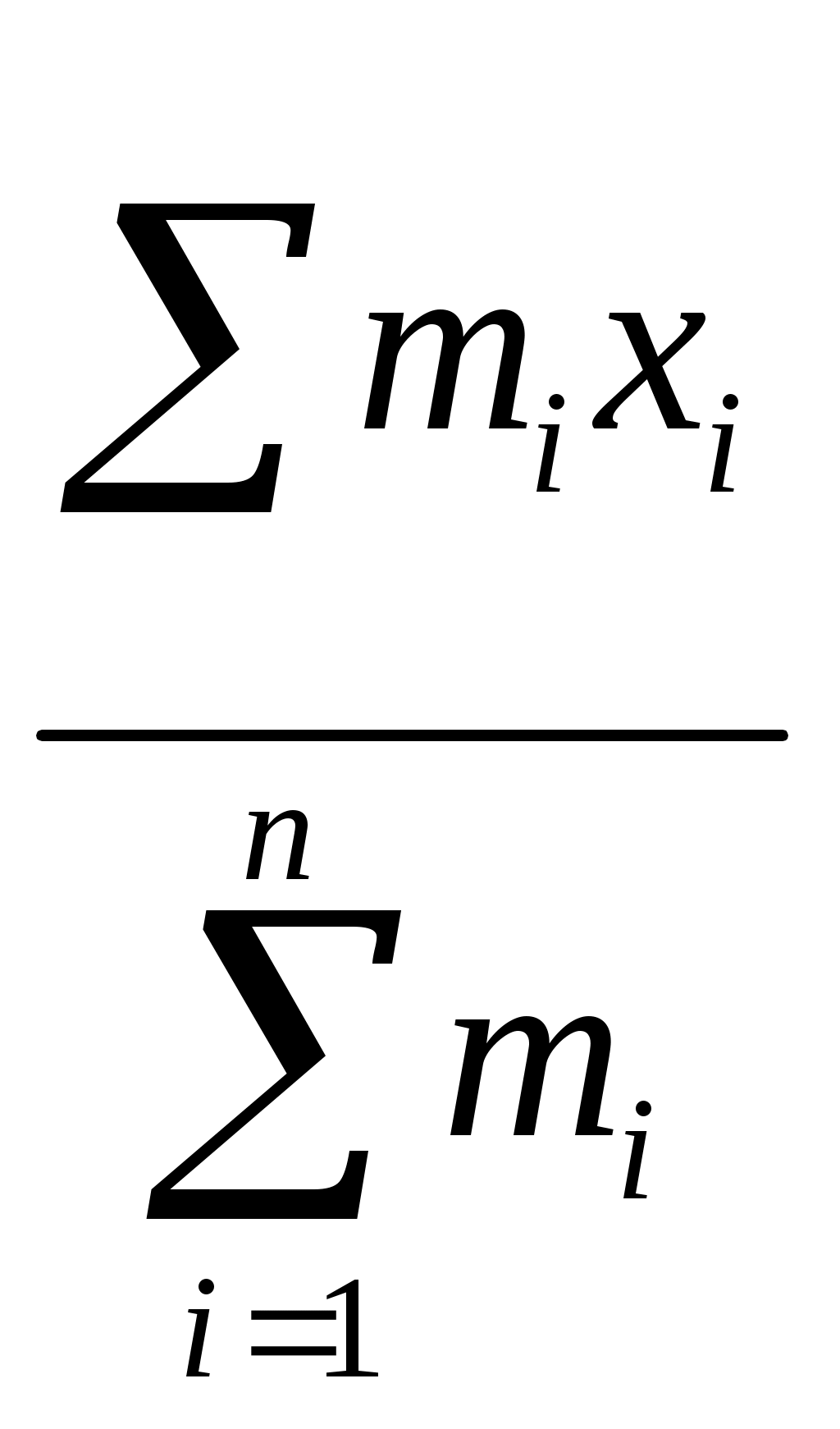= = , (31)

где m_i –частота; = N –число всех зафиксированных значений x_i.

Средняя взвешенная подсчитывается также сумма произведений значений случайной величины x

---

_i на соответствующие им частости m_i / N , т.е.

= W ₁x ₁+W ₂x ₂+ + W _nx_n = (32)

При достаточно большом числе испытаний N частости приближенно равны соответствующей вероятности

W₁ ≈ P₁ ; W₂ ≈P₂ ; W_n ≈ P_n; (33)

Заменив в формуле относительные частоты соответствующими вероятностями, получим для дискретной случайной величины равенство для определения математического ожидания:

MX ≈ P₁ x₁+ P₂ x₂ + + P_n x_n= ∑P_i x_i (34)

2) Размах R распределения (диапазон распределения) в эмпирической совокупности – разность между максимальным и минимальным из значений случайной величины x_i ,полученных в результате испытаний.

Им пользуются в эмпирических распределениях как мерой рассеивания при малом числе испытаний(N < 10).

Рассеивание случайной величины наиболее часто измеряют дисперсией(рассеиванием) и средним квадратическим отклонением.

3) Эмпирическая дисперсия S² - величина рассеивания зафиксированных значений вокруг их среднего значения. При малом числе наблюдений т.е. при N < 25, S² = (35)

При N > 25 S² = = a₂ - , (36)

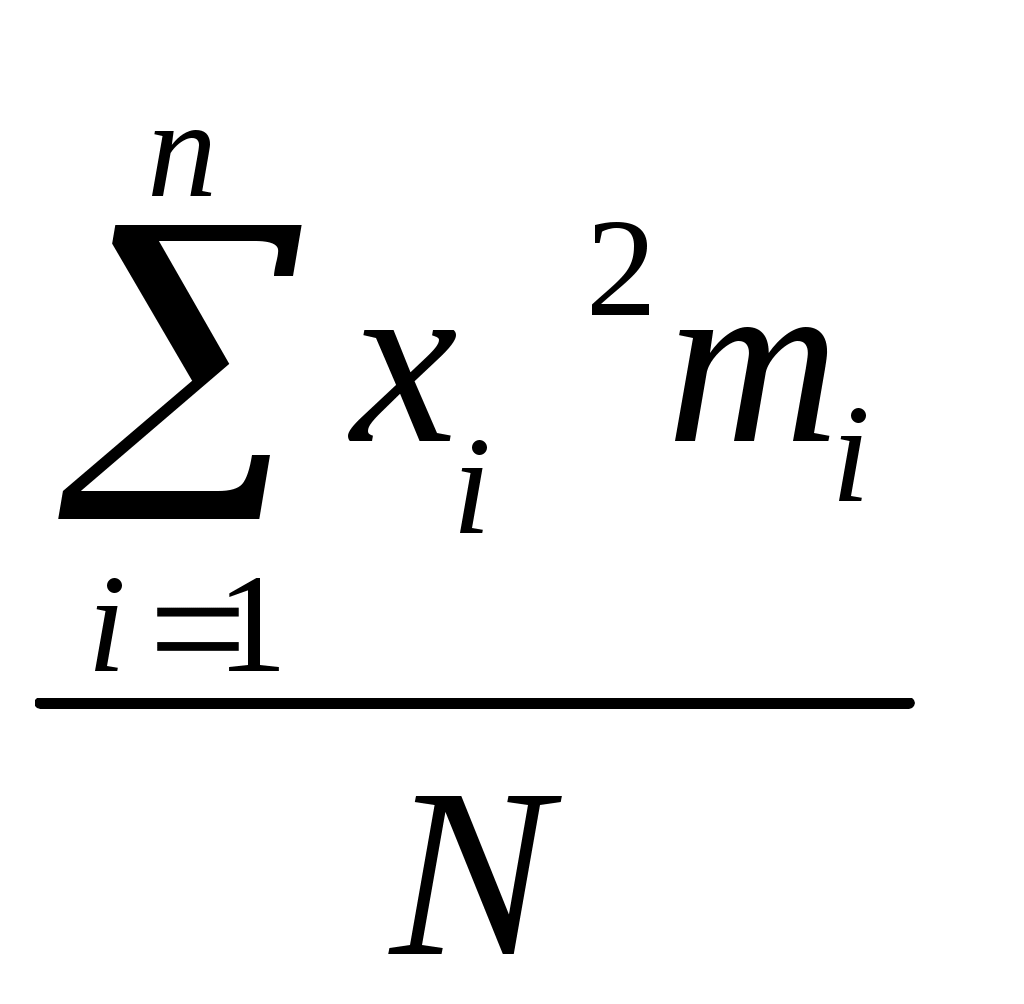где а₂ = (37)

Эмпирическое среднее квадратическое отклонение и среднее квадратическое отклонение (стандарт) будут соответственно равны корням квадратным из дисперсии S² и из DX.

Размерности S и σ совпадают с размерностью самой случайной величины х.

σ = и определяет ширину кривой распределения.

4) Мода М₀ эмпирической совокупности - это значение непрерывной случайной величины х

---

Смотрите также файлы

• Какой внешний долг южной кореи.docx

• Особенности производства в отношении отдельных категорий лиц.docx

• Практическая работа 11 Управление системой компас3d цель приобрести навыки управления системой компас3d план.docx

• Студенты, чья фамилия начинается с букв аг, выполняют первый.docx

• Практическая работа 5 По дисциплине Физика Земли (наименование учебной дисциплины согласно учебному плану) Тема Выполнение геологической интерпретации фрагмента регионального геофизического профиля мовогт (геотраверса) Уралсейс.docx