Конец 20-х — середина 80-х годов XX ст. После Первой мировой войны начался процесс качественных изменений системы мирового хозяйства, который завершился падением колониальной системы.

Конец 80-х — начало 90-х годов XX ст. Отличительной особенностью этого этапа является нарастание интеграционных процессов в производстве, развитие их организационно-экономических форм, связанных с производством товаров и комплектующих в разных странах.

В целом мировое хозяйство в конце XX — начале XXI века, сохраняя разнообразие, большое количество противоречий и разноплановых тенденций, всё же является более целостным, интегрированным и динамичным, чем в середине XX века, и приобретает глобальный характер. Для него стали характерными новые экономические связи и отношения, расширились таможенные и политические союзы.

Характеристика современного этапа развития мирового хозяйства: - на основе дальнейшего развития международного разделения труда в мире происходит интенсивный процесс интернационализации и глобализации экономических отношений, усиливается экономическая интеграция; - научно-технический прогресс привел к глубоким изменениям в самой структуре мирового хозяйства, еще более усилилась трансформация различных сфер международных экономических отношений; - каждая из национальных экономик стремится увеличить свою экспортную квоту и все в большей степени зависит от успехов в международной экономической деятельности; - мировые рынки товаров и услуг растут значительнее, чем их производство; - наиболее динамично развивающимися секторами международных отношений становятся услуги, включающие в себя информатику, ноу-хау, инжиниринг, образование, финансовые услуги; и т.д.

2. 
   Международная экономическая интеграция: предпосылки, цели, этапы интеграции. Россия в интеграционных группировках
   

Международная экономическая интеграция (МЭИ) – это сближение, взаимоприспособление, сращивание национальных хозяйственных систем. Интеграция является объективным, осознанно направляемым процессом, принимающим форму межгосударственных соглашений.

Предпосылки интеграции: - идентичность уровней экономического развития и рыночной зрелости объединяющихся стран; - географическая близость, наличие, как правило, общей границы, исторически сложившихся экономических взаимосвязей; -·общность социально-экономических, политических и иных проблем, стоящих перед интегрирующимися странами.

---

Цели интеграции: - увеличение объемов производства и расширение номенклатуры поставляемых товаров и услуг; - реализация преимуществ экономики масштаба; - формирование благоприятной внешнеполитической среды; - решение задач торговой политики; - содействие структурной перестройке национальных экономик; - поддержка отдельных отраслей промышленности, сферы услуг, сельского хозяйства.

Выделяют четыре вида (этапа) международной экономической интеграции:

1. Зона свободной торговли (ЗСТ) – первая интеграционная ступень, предусматривающая договоренность между государствами по поводу свободной от таможенных и количественных ограничений международной торговли товарами и услугами.

2. Таможенный союз (ТС) возникает на основе соглашений государств-участниц о полном упразднении таможенных пошлин при взаимообмене товарами и услугами. Кроме того, ТС предполагает создание единого для всех стран-участниц внешнего таможенного тарифа.

3. Единый рынок (ЕР) представляет более совершенную форму экономической интеграции, чем ЗСТ и ТС. Помимо всего, имевшего место на предыдущих уровнях, он предусматривает унификацию технических норм, единых экологических требований, а также единой законодательной базы для внутрисоюзного предпринимательства.

4. Экономический Союз (ЭС) – высшая форма современной межгосударственной интеграции. Он представляет собой объединение государств на основе создания единого экономического, правового, военного и информационного пространства.

Россия в интеграционных группировках:

• 
  Союзное государство
  
• 
  ООН (Совет Безопасности ООН)
  
• 
  СНГ
  
• 
  ОДКБ
  
• 
  Организация по безопасности и сотрудничеству в Европе
  
• 
  Организация черноморского экономического сотрудничества
  
• 
  Совет Европы
  
• 
  Большая восьмёрка
  
• 
  БРИКС
  
• 
  АТЭС
  
• 
  Шанхайская организация сотрудничества
  
• 
  Евразийский экономический союз
  
• 
  Центрально-Азиатское сотрудничество (организация)
  
• 
  Международная организация по стандартизации
  
• 
  Международный олимпийский комитет
  
• 
  Международная электротехническая комиссия
  
• 
  Всемирная торговая организация
  

Эконометрика

1. 
   Метод наименьших квадратов: предпосылки, математическая формулировка метода, свойства оценок
   

Метод наименьших квадратов (МНК) – один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Данный метод применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

---

Предпосылки:

1. Математическое ожидание случайного отклонения равно нулю для всех наблюдений.

2. Дисперсия случайных отклонений постоянна для любых наблюдений.

3. Случайные отклонения ui и uj являются независимыми друг от друга для i¹j.

4. Случайное отклонение должно быть независимо от объясняющих переменных.

5. Модель является линейной относительно параметров.

Математическая формулировка:

Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение.



То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.

Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.

Свойства оценок МНК определяются предположениями относительно свойств случайного возмущения в модели наблюдений. Эти предположения обычно называются условиями Гаусса – Маркова.

Условия Гаусса-Маркова:

1. 
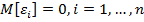   – условие, гарантирующее несмещённость оценок МНК.
   

1. 
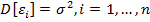   – условие гомоскедастичности, его нарушение приводит к проблеме гетероскедастичности.
   
2. 
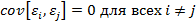   – условие отсутствия автокорреляции предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях. Если данное условие не выполняется, то в модели возникает проблема автокорреляции случайных возмущений.
   
3. 
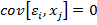   для всех 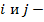условие независимости случайного возмущения и объясняющей переменной. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.
   

---

Свойства оценок, полученных с помощью МНК:

1. Линейность оценок – оценки параметров и представляют собой линейные комбинации наблюдаемых значений объясняемой переменной;

2. Несмещённость оценок;

3. Состоятельность оценок;

4. Эффективность – данное свойство означает, что оценка имеет минимальную дисперсию в заданном классе оценок.

2. Модель парной линейной регрессии: формулировка, область применения, мнк-оценки, примеры использования.

Линейная регрессия - выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины.

В отличие от функциональной зависимости y = f(x), когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.

Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.

Если установленная зависимость может быть записана в виде уравнения прямой

y = ax + b, то эта регрессионная зависимость называется линейной регрессией.

О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).

---

В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель

,

где - свободный член прямой парной линейной регрессии,

- коэффициент направления прямой парной линейной регрессии,

- случайная погрешность,

N - число элементов генеральной совокупности.

Метод наименьших квадратов является одним из наиболее распространенных и наиболее разработанных, вследствие своей простоты и эффективности методов оценки параметров линейных эконометрических моделей. Вместе с тем, при его применении следует соблюдать определенную осторожность, поскольку построенные с его использованием модели могут не удовлетворять целому ряду требований к качеству их параметров и, вследствие этого, недостаточно «хорошо» отображать закономерности развития процесса .

Процедура оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением: yt = a0 + a1 х1t +...+ an хnt + εt .

Исходными данными при оценке параметров a0 , a1 ,..., an является вектор значений зависимой переменной y = (y1 , y2 , ... , yT )' и матрица значений независимых переменных



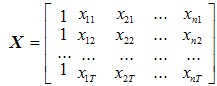
в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели .

Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.

---

Смотрите также файлы

• Свод правил республики казахстан.pdf

• Лабораторная работа по дисциплине правоведение Группа Тм22УП161в Студент Кузьмин Н. С. Преподаватель Рогова Т. М.docx

• 1. Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей.doc

• Тема Основы здорового образа жизни.doc

• 5 Сгибание и разгибание рук в упоре лежа.docx