Файл: пензенский государственный университет политехнический институт.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Диссертация

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 215

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Содержание

Введение

Основные положения, выносимые на защиту:

Эквивалентные преобразования моделей задач линейного программирования

Анализ моделей и алгоритмов решения задач о назначениях

Анализ эквивалентных преобразований моделей задач о назначениях

Выводы

Модель и алгоритм решения задачи с приоритетными назначениями

Выводы

Алгоритм решения простейшей линейной многокритериальной задачи о назначениях Многообразие многокритериальных задач в сочетании с отсутствием единого принципа оптимальности порождает огромное число методов их решению. Использование того или иного подхода к решению конкретной задачи может оказать существенное влияние на трудоемкость вычислений. Это относится особенно к специальным классам задач, для которых при скалярном критерии качества разработаны эффективные алгоритмы, использующие специфику ограничений и критериальной функции. Одной из таких задач является задача о назначениях.В основе подавляющего большинства методов решения многокритериальных задач лежит понятие веса критерия, характеризующего его сравнительную важность. Наиболее распространенные методы решения многокритериальных задач основаны на свертке набора исходных целевых функций (с учетом их веса) в один обобщенный скалярный критерий [71]. Такой подход позволяет получить оптимальное по Парето решение и при этом характеризуется вычислительной эффективностью. Использование свертки обеспечивает возможность применения для решения многокритериальной задачи о назначениях специально разработанные для однокритериального случая методы – венгерский и метод Мака.Свертка частных критериев разного смыслового содержания не позволяет интерпретировать значение взвешенного обобщенного критерия, поэтому в общем случае использование операторов свертки требует предварительного нормирования матриц затратСl,l 1, k, т.е. приведения их к единой безразмерной шкале. Часто используемый способ нормирования – минимакс-нормализация.Предлагается следующий алгоритм решения простейшей многокритериальной линейной задачи о назначениях (70) – (75). Нормировать матрицы затрат Сl, l 1, k: cl clсl ijmin . c  cijl maxlmin Составить целевые функции безразмерными коэффициентами: f1(X), f2 (X),..., fk(X) с n nlfl(X)  сijxij, l 1, ki1 j1 Составить вектор   (1, 2,..., k)весовых коэффициентов относительной важности целевых функцийf1(X), f2 (X),..., fk(X) ,l 0 , l 1.k, l 1. В том случае, если все критерии имеют одинаковуюl1 важность,l 1, l 1.k. Составить скалярную целевую функция (обобщенный критерий) g(X)   ) ,( f1(X), f2 (X),..., fk(X),где  – оператор свертки. Перейти к однокритериальной задаче о назначениях вида g(X)  min, (76) n xij 1, j 1, n,i1 (77) n xij 1, i 1, n,j1 (78) xij{0,1}, i, j 1, n. (79) Решить задачу (76) – (79) венгерским методом или методом Мака. Результатом является получение решения, оптимального по Парето. Решая задачу многократно и с изменением весовых коэффициентов, можно получить множество Парето-оптимальных решений. Вид свертки в каждом конкретном случае отражает приемлемую для ЛПР форму компромисса между частными критериями. Наиболее часто используемыми свертками являются линейная свертка, мультипликативная свертка и свертка на основе отклонения от идеальной точки. 1   ...   8   9   10   11   12   13   14   15   ...   21

Решение простейшей линейной многокритериальной задачи о назначениях с использованием свертки на основе отклонения от идеальной точки Под идеальной точкой в многокритериальной задаче о назначениях вида (71) – (76) понимают такой векторF*(X)  Rk, компоненты которого являются минимумами целевых функцийf1(X), f2 (X),..., fk(X) по отдельности, т.е.fl*(X)  min fl(X),XDl 1, k. В практических задачах идеальная точка является недостижимой [73]. Свертка на основе идеальной точкиF*(X)имеет вид: g(X)  (F(X), F*(X)) , где  – некоторая метрика вRk. Наиболее часто используются взвешенная чебышевская метрика g(X)  maxlfl(X)  fl* l (80) и взвешенная евклидова метрика kg(X)  ( fl(X)  fl*)2.l1 (81) Предлагается следующий алгоритм составления обобщенного скалярного критерия на основе идеальной точки: составить kоднокритериальных задач о назначениях вида n nlfl(X)  cijxij min,i1 j1n (82)  xij 1, j 1, n,i1n (83)  xij 1, i  1, n,j1 (84) xij{0,1}, i, j 1, n, (85) гдеl 1,k; найти X * – оптимальное решение l-й задачи вида (82) – (84) и lfl*  fl(X*) , l 1, k; lсоставить вектор F*(X)  ( f*, f*,..., f*) , гдеfl*  fl(X*) , l 1, k;1 2 k lсоставить свертку на основе отклонения от идеальной точки по формуле (80) или (81). Разработана программа для нахождения решения многокритериальной линейной задачи о назначениях с использованием свертки на основе отклонения от идеальной точки средствами математического пакета Mathcad, полный текст которой представлен в приложении E. На рисунке 20 приведены результаты применения свертки на основе отклонения от идеальной точки к многокритериальной задаче о назначениях, исходные данные которой совпадают с исходными данными задачи, решенной с использованием линейной свертки: Рисунок 20 – Результаты решения многокритериальной линейной задачи о назначениях с использованием свертки на основе отклонения от идеальной точки На рисунке 20 представлены матрица X – оптимальное по Парето решение, полученное с использованием чебышевской метрики, и матрица Y – оптимальное по Парето решение, полученное с использованием евклидовой метрики. Также программа находит для каждого оптимального по Парето решения значения соответствующего ему критериального вектора. Применяя алгоритм многократно с изменением весовых коэффициентов, можно построить множество точек Парето. Выбор конкретного решения из множества Парето-оптимальных осуществляется ЛПР.Следует отметить, что в некоторых прикладных задачах ЛПР за идеальную точку может принять реальное решение, соответствующее некоторым принятым стандартам или планируемым значениям. 1   ...   10   11   12   13   14   15   16   17   ...   21

Модель и алгоритм решения многокритериальной задачи о назначениях с целевыми функциями противоположного направления

Модель и алгоритм решения многокритериальной открытой задачи о назначениях Обобщим открытую задачу о назначениях на случай многокритериальности. Математическая модель такой задачи в предположенииm nимеет вид:

Модель и алгоритм решения многокритериальной задачи с порядком назначений Обобщим задачу с порядком назначений на случай многокритериальности. Математическая модель такой задачи имеет вид:nn f1(X)  c1 x min,(121) ijiji1 j1… nn k(X)  ckx min,n (122)  xij 1,n j 1, n, (123)  xij 1, i  1, n, (124) {0,1}, i1, n, j 1, n, , i1, n, j h1, n, j*  1, h. (126) f xij гдеP {1,2,.., h}пр.(i, j)  (i, j*)– подмножество индексов работ, распределяемых в первую очередь.В главе 2 показано, что однокритериальная задача с порядком назначений эквивалента совокупности двух последовательно решаемых задач – открытой и с недопустимыми назначениями. Аналогично, многокритериальная задача с порядком назначений эквивалента совокупности двух последовательно решаемых задач – многокритериальной открытой задаче и многокритериальной задаче с недопустимыми назначениями. Следовательно, можно описать алгоритм решения многокритериальной задачи с порядком назначений. Нормировать матрицы затрат Сl, l 1, k: cl clсl ijmin . c  cijl maxlmin Найти размер штрафа Ml 2n. Построить математическую модель назначения на работы из множества P :

Выводы

Заключение

Список использованных источников


i1 j1




xij

i1


n




xij

j1

1,
1,

j 1, n,



i 1, n,




где

xij{0,1}, i, j 1, n,


ij
Ql (ql) – матрица затрат l-й задачи с недопустимыми назначениями,



l 1, L.

Матрица затрат Ql

образом:

получается из исходной матрицы С следующим


– в каждой комбинации Rн. к. ,


k
k

k1, K, фиксируется пара индексов,


обозначим ее как

(i, j)* ;

– в матрице затрат на данное место ставится штраф, в качестве

которого можно взять число

M n maxсij.


Для определенности будем полагать

получаем

M 2n max сij. В результате

M, если (i, j) Rн. к.,

(i, j) (i, j)* , k 1, K;


ij
ql

cij

kk

иначе.

Определим количество Lполученных задач. Зафиксировать пару


индексов в комбинации
индексов в комбинации

н. к. 1

R
R
н. к. 2

можно
можно

н. к. 1

R
R
н. к. 2

способами, зафиксировать пару
способами и т.д. По основному


правилу комбинаторики получаем

L | Rн. к. | | Rн. к. | ... | Rн. к. | .

1 2 K

Каждую из полученных задач можно решить венгерским методом или методом Мака. Оптимальным решением является та матрица назначений,

которой соответствует минимальное значение целевой функции




l 1, L.

l(X) ,

Эквивалентное преобразование задачи с недопустимыми комбинациями в совокупность L простейших линейных задач с формулируется так:

  1. найти размер штрафа

M 2n max сij;



  1. k
    R
    последовательно фиксируя в каждой комбинации индексов (i, j)* , построить Lпростейших линейных задач

н. к. k

пару





nn

l(X) qlxij min,

ij

i1 j1
n
(43)

xij 1, j 1, n,

i1

n
(44)

xij 1, i 1, n,
(45)



j1


xij{





0,1}, i, j 1, n,
(46)

l1, L,
(47)



где

L | Rн. к. | | Rн. к. | ... | Rн. к. |;

1 2 K



ql M, если (i, j)  Dk,

(i, j) (i, j)* , k 1, K;

k


c
ij

ij

иначе.

Тогда алгоритм решения задачи о назначениях (38) – (42) имеет вид.

  1. Применить к модели (38) – (42) эквивалентное преобразование задачи с недопустимыми комбинациями. Результатом является получение L простейших линейных задач вида (43) – (47).

  2. Решить L задач, описываемых соотношениями (43) – (47), венгерским методом или методом Мака.

  1. Найти

min l(X). Матрица назначений X , соответствующая

l1, L

min l(X), является оптимальным решением задачи с недопустимыми

l1, L
комбинациями назначений.

Разработана программа для нахождения решения задачи с недопустимыми комбинациями назначений средствами математического пакета Mathcad. Рассмотрим работу программы на исходных данных, представленных на рисунке 8.



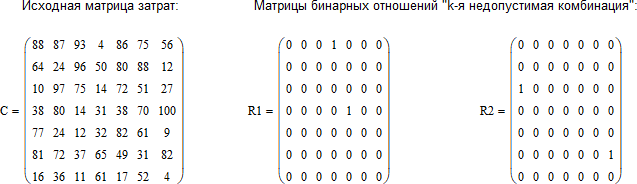
Рисунок 8 – Исходные данные задачи с недопустимыми комбинациями назначений

Применяя описанный выше алгоритм, находим оптимальное решение (рисунок 9).



Рисунок 9 – Результаты поиска оптимального решения задачи с недопустимыми комбинациями назначений
При заданных матрице затрат и множестве недопустимых комбинаций целевая функция задачи с недопустимыми комбинациями назначений достигает минимального значения, равного 112.

Важно отметить, что в общем случае учет недопустимых комбинаций назначений ведет к увеличению значение целевой функции. На рисунке 10 приведено решение простейшей линейной задачи о назначениях, матрица

затрат C которой совпадает с матрицей затрат задачи с недопустимыми комбинациями назначений:


Рисунок 10 – Результаты поиска оптимального решения простейшей линейной задачи с матрицей затрат С
Как видно из рисунка, при одинаковой матрице затрат минимальное значение целевой функции простейшей линейной задачи о назначениях меньше минимального значения целевой функции задачи с недопустимыми комбинациями назначений.

Наложим на задачу (38) – (42) дополнительное ограничение. Будем считать, что в искомом решении может присутствовать не более одного назначения из каждой недопустимой комбинации. Эквивалентное преобразование будет иметь отличие лишь в части правила размещения

штрафов в матрицах Ql:

M, если (i, j) Rн. к.,
(i, j) (i, j)* , k 1, K;


ij
ql

cij

kk

иначе.


где

l 1, L,

L | Rн. к. | | Rн. к. | ... | Rн. к. | .

1 2 K

Такой способ построения матриц затрат позволит исключить из искомого решения все назначения из недопустимой комбинации, кроме

одного. В общем случае, полагая, что в искомом решении может

присутствовать hназначений из каждой недопустимой комбинации,

h min| Rн. к. |,| Rн. к. |,...,| Rн. к. |., штрафы будут последовательно

1 2 K


накладываться на размещения из hэлементов комбинации

Rн. к. .

k



Смотрите также файлы