Файл: Зубодолбежный станок.docx

4. 
   Исследование функции положения прототипа 2
   

По графику изменения координаты выходного звена найдём крайнее положение при помощи встроенных функций MathCAD (нижний правый график на рисунке 1.6.3.1).



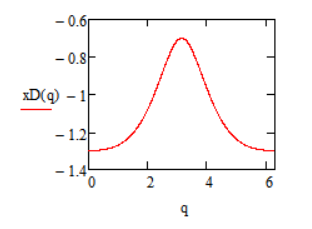
Рис.1.6.4.1. График изменения координаты точки D.







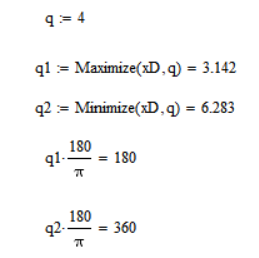
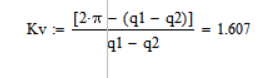
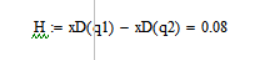
Значение Kv по заданию 1.6, H по заданию 0,08, следовательно, удалось добиться желаемого результата.

5. 
   Расчёт критериев синтеза
   
   1. 
      K1
      

Найдём максимальное по модулю значение скорости выходного звена и рассчитаем критерий K1.

2. 
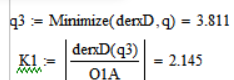
   K2
   

Найдём максимальное по модулю значение косинуса угла 4-ого звена и рассчитаем критерий K2.

6. 
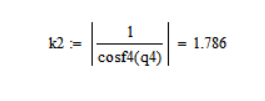
   Крайние положение прототипа 2
   

Крайние положения механизма изображены на рисунке 1.6.6.1.


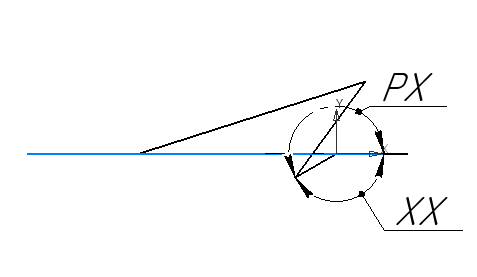
Рисунок 1.6.6.1 – Крайние положение прототипа 2

7. 
   Таблица сравнения. Выбор лучшего прототипа.
   

Таблица 1 - Таблица сравнения прототипов

	Kv	H	K1	K2	Габариты (мм)
Прототип 1	1.6	0.08	1,139	1.208	378х218
Прототип 2	1.607	0.08	2,45	1,786	218х273

---

Из таблицы видно, что очевидного выбора нет (необходимо выбрать прототип с меньшими K1,K2, габаритами). Так что необходимо установить приоритетный параметр: наиболее важным параметром я выбрала K1, так как этот коэффициент отражает соотношение между силами на входе и на выходе: сила, прикладываемая к выходному звену в зубодолбежном станке, очень велика, а потому важно не допустить возрастания момента на кривошипе, так как он и так велик. Учитывая это, я выбрала для дальнейшего рассмотрения прототип 1.

8. 
   План двенадцати положений выбранного механизма
   

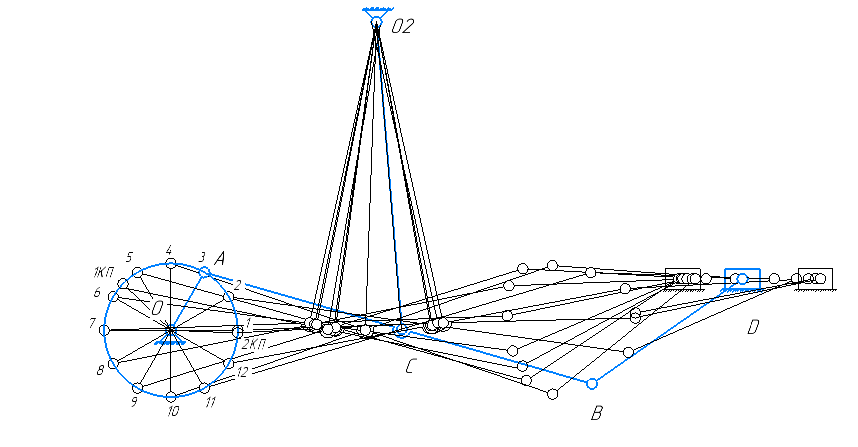
Рисунок 1.8.1 – 12 положений механизма

9. 
   Графоаналитическое исследование кинематики выбранного прототипа
   
   1. 
      Построение плана скоростей и ускорений положения 60°
      

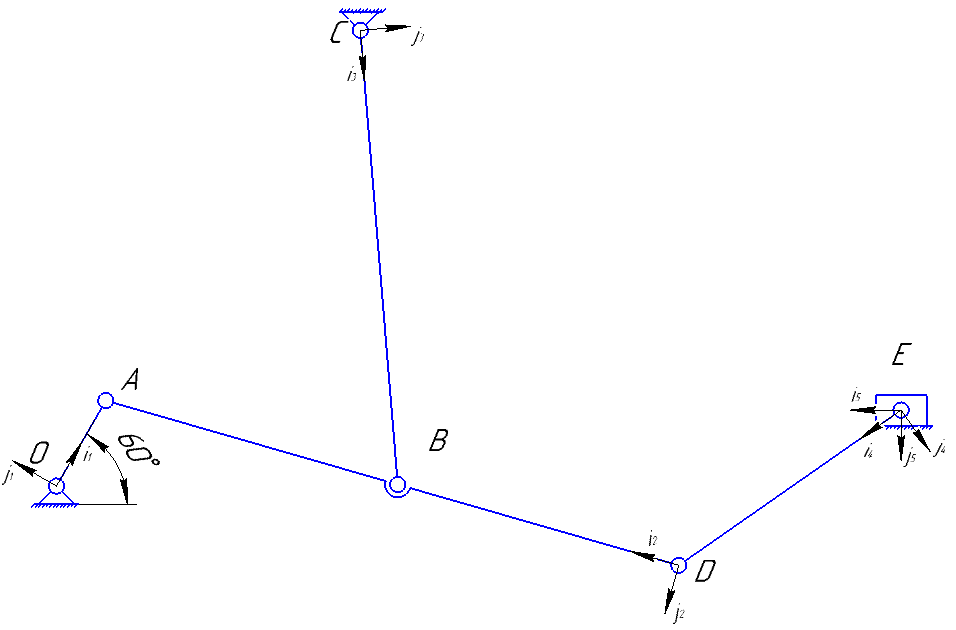
Рисунок 1.9.1.1 – Схема механизма в положении 60°

План скоростей представлен на рисунке 1.9.1.2.



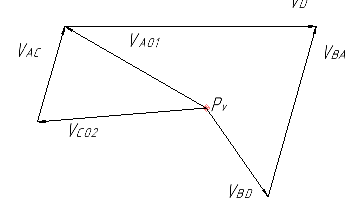
Рисунок 1.9.1.2 – План скоростей

План ускорений представлен на рисунке 1.9.1.3.



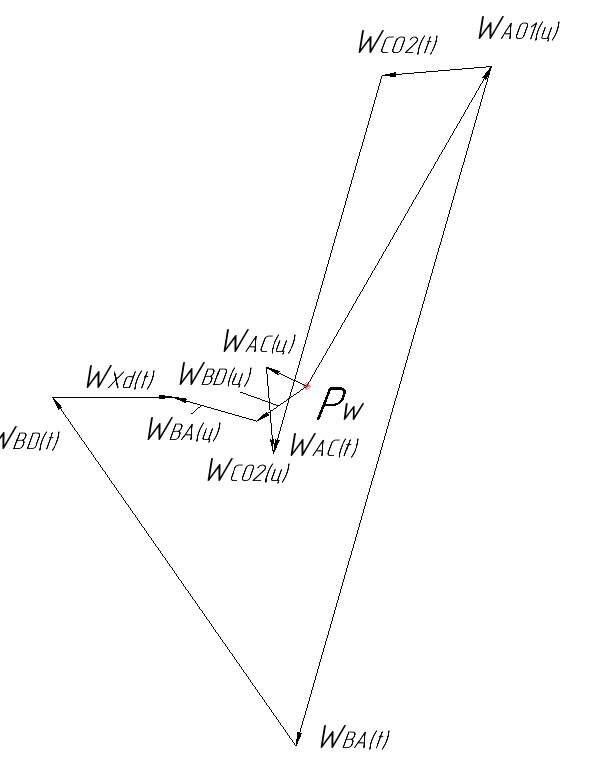
Рисунок 1.9.1.3 – План ускорений

Рассчитаем скорости и ускорения графически с помощью MathCAD и КОМПАС:

2. 
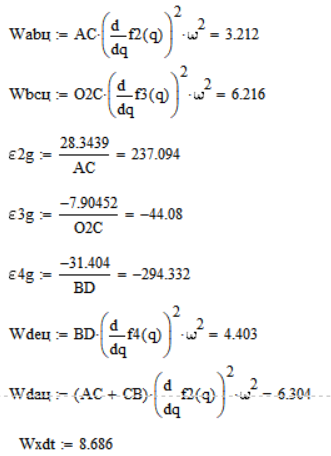
   Расчёт скоростей и ускорений аналитически
   положения 60°
   

3. 
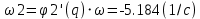
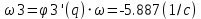
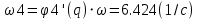
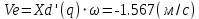
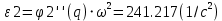
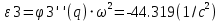
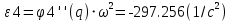
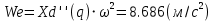
   Сравнение результатов расчётов для положения 60°
   

---

Таблица 2 – Сравнение результатов двух методов расчёта положения 60°

Координаты и углы	Аналитически	Графически
Скорости
ω2	-5.183 с-1	-5.184 с-1
ω3	-5.886 с-1	-5.887 с-1
ω4	6.328 с-1	6.424 с-1
Xe	-1.5677 м/с	-1.567 см/с
Ускорения
ε2	237.094 с-2	-241.217 с-2
ε3	-44.08 с-2	-44.319 с-2
ε4	-294.332 с-2	-297.256 с-2
We	8.686 м/c2	м/c2

Силовой анализ механизма. Снижение внешней виброактивности механизма.

10. 
    Определение исходных данных для силового расчёта
    

Погонная масса: µ = 50 кг/м

Ускорение свободного падения: 10 м/с²

Угловая скорость вращения кривошипа: 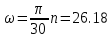м/с

Массы звеньев (кг):



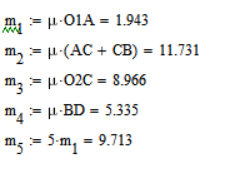
Силы тяжести рассчитываются по формуле:

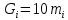
Определим координаты центров масс. Для этого запишем уравнения координат точек А, B, D:



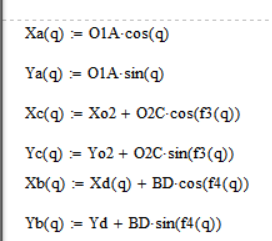
Далее определим координаты центров масс по следующим формулам:



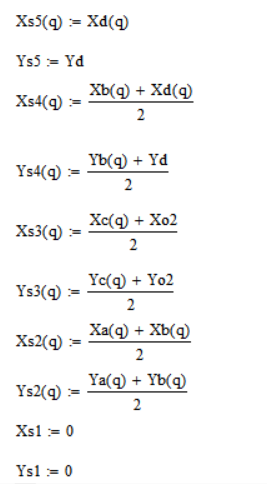
Определение сил инерции (Н):

---

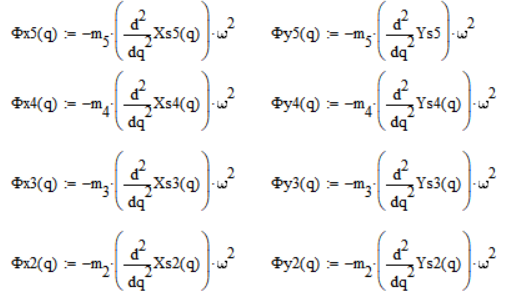
Определение моментов инерции (кг*м²):



Определение моментов сил инерции (Н*м²):

11. 
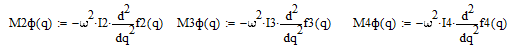
    Определение зависимости силы сопротивления от обобщенной координаты
    

По индикаторной диаграмме, представленной на рисунке 1.2.1, определяется зависимость рабочей нагрузки от входной координаты q.

Результаты вычислений представлены на рисунках ниже:

Задание функции положения выходного звена:





Задание функции величины рабочей нагрузки в зависимости от функции положения:





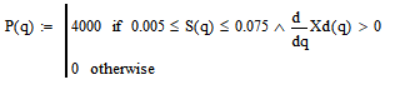
График функции рабочей нагрузки, совмещённый с графиков скорости выходного звена, представлен на рисунке 2.2.1.



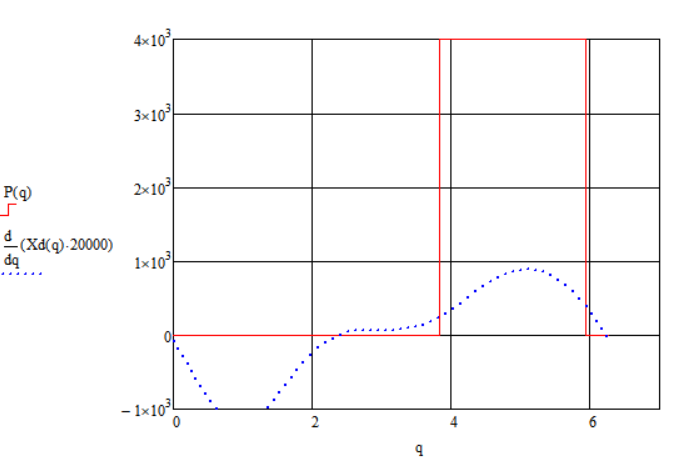
Рисунок 2.2.1 – График функций рабочей нагрузки и скорости выходного звена



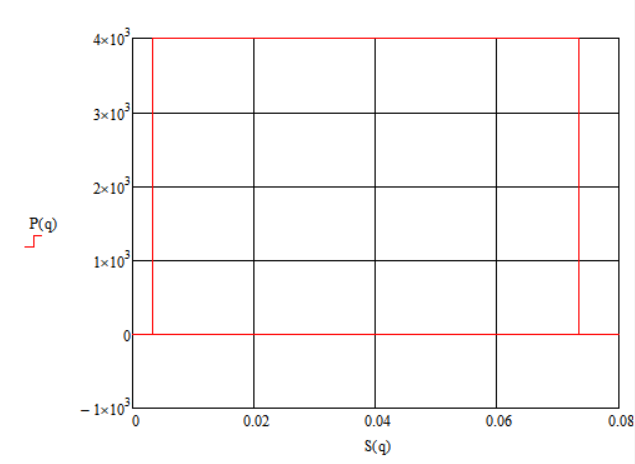
Рисунок 2.2.2 – График зависимости рабочей нагрузки от функции положения выходного звена (индикаторная диаграмма)

12. 
    Кинетостатический расчёт
    
    1. 
       Составление и решение уравнений кинетостатики
       

На схеме механизма, показанной на рисунке 2.3.1.1, изобразим все силы инерции, силы тяжести и моменты сил инерции для всех звеньев механизма.



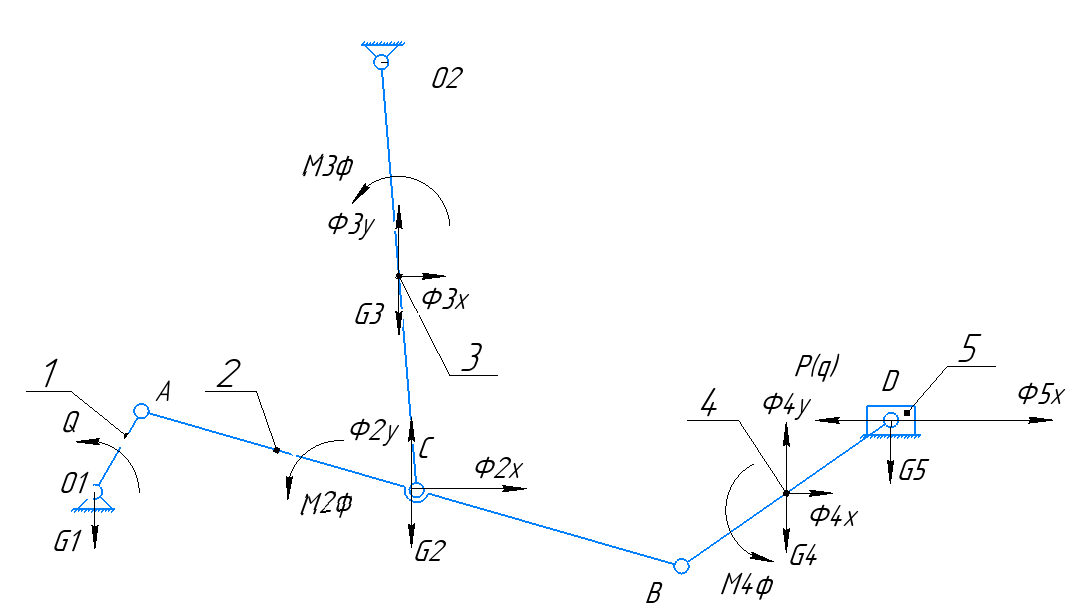
Рисунок 2.3.1.1 – Схема механизма для кинетостатического расчёта

Рассмотрим отдельно структурные группы механизма. Отрываем структурную группу от механизма и в местах отрыва действие других звеньев заменяем реакциями опор.

Звенья 5 и 4:


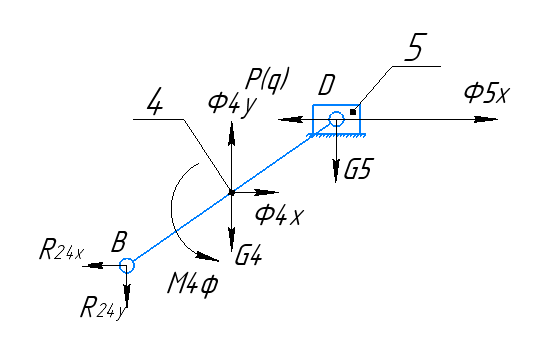
Рисунок 2.3.1.2 – Звенья 4, 5

Запишем уравнения равновесия для плоской системы:

---

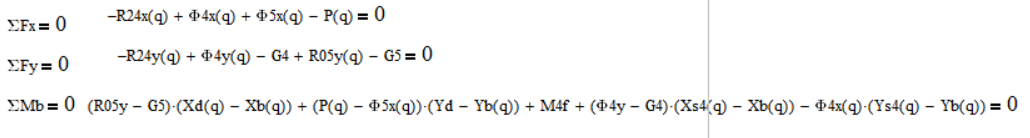
Из выше представленных уравнений выразим неизвестные реакции:



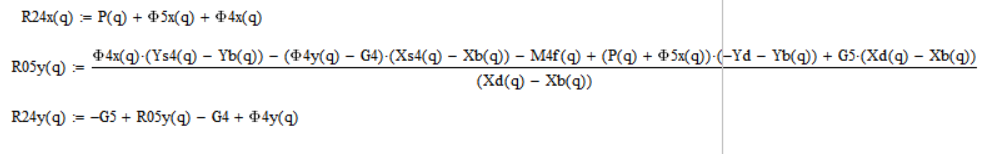
Звенья 3 и 2:


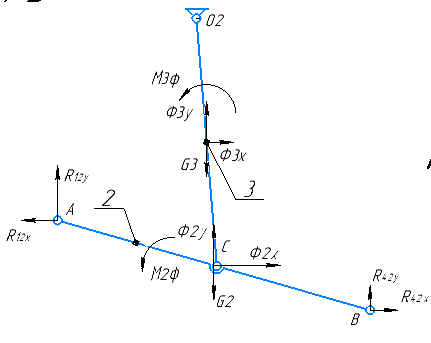
Рисунок 2.3.1.3 – Звенья 2, 3

Определим реакции для звеньев 3 и 2. Для этого запишем уравнения равновесия для плоской системы:



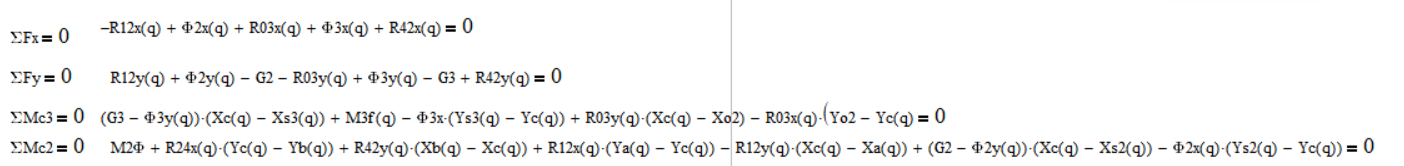
Учтём:



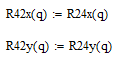
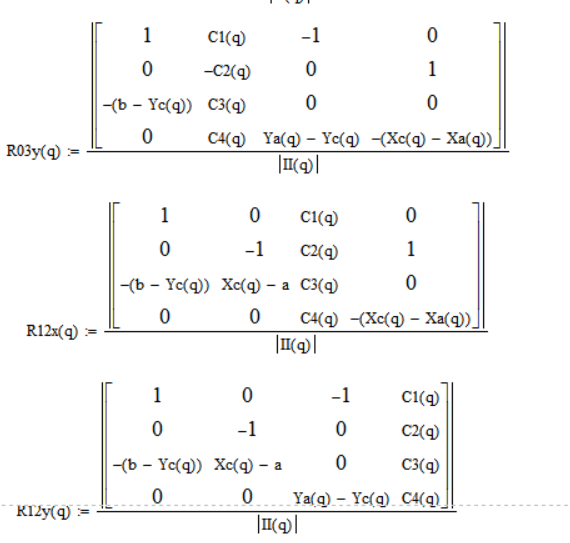
Из выше представленных уравнений выразим неизвестные реакции методом Крамера:





Звено 1:


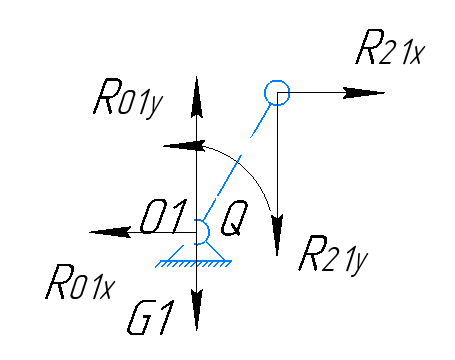
Рисунок 2.3.1.4 – Звено 1

Определим реакции для звена 1. Для этого запишем уравнения равновесия для плоской системы:



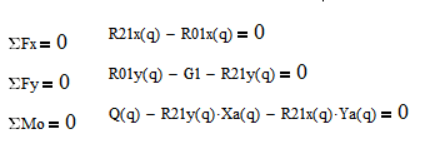
Учтём:



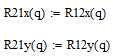
Из выше представленных уравнений выразим неизвестные реакции:

2. 
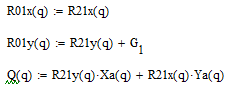
   Нахождение движущего момента из общего уравнения динамики
   

Для механизма работа активных сил равна:



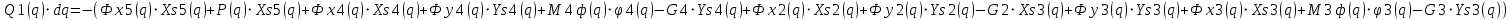
Найдём движущий момент:









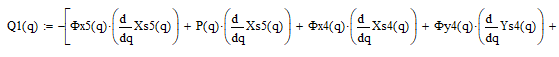
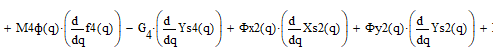
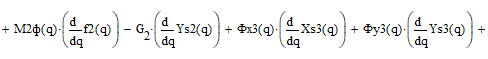
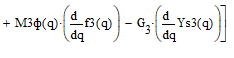
Для проверки кинетостатического анализа наложим графики зависимостей, полученных из общего уравнения динамики и из кинетостатического расчёта, движущего момента от входной координаты (рисунок 2.3.2.1).

---