Файл: Зубодолбежный станок.docx

Коэффициент при синусе в разложении приведённого момента инерции:



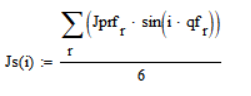
Выражение разложения приведённого момента инерции в ряд Фурье с точностью до 5 гармоник:



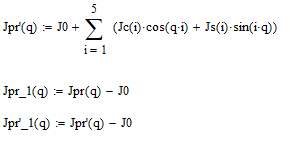
Переменные части приведённых моментов инерции:




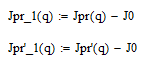
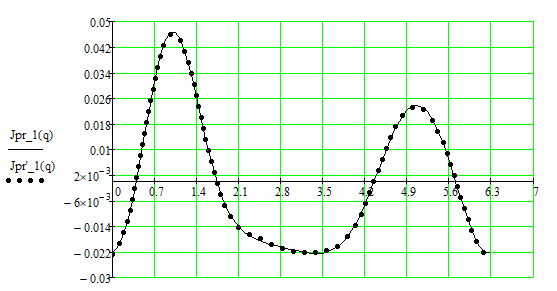
Рисунок 4.3.1.1 – Совмещённый график переменных частей приведённого момента инерции и его разложения в ряд Фурье

Определим первую производную по обобщённой координате приведённого момента инерции по следующей формуле:





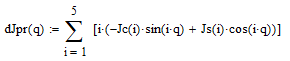
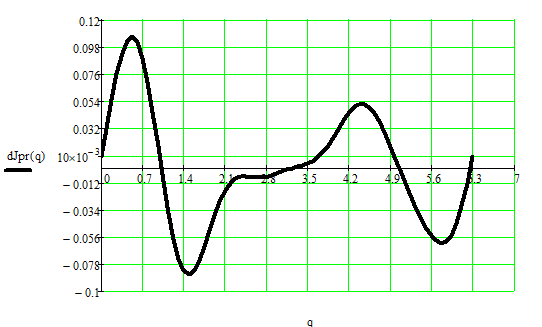
Рисунок 4.3.1.2 – График первой производной приведённого момента инерции по обобщённой координате

2. 
   Приведённый момент сил сопротивления
   

Приведённый момент сил сопротивления определяется как коэффициент при вариации обобщённой координаты в выражении для возможной работы активных сил сопротивления (рабочей нагрузки и силы тяжести):



Определение коэффициентов разложения в ряд Фурье приведённого момента инерции:



Выражение разложения в ряд Фурье приведённого момента сопротивления:





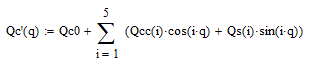
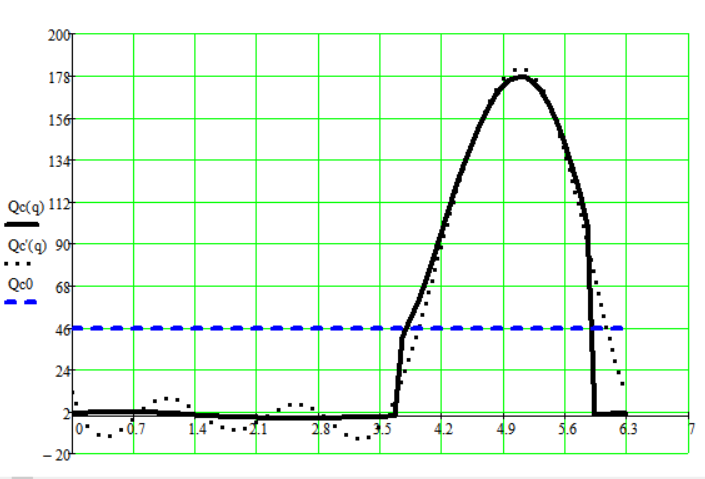
Рисунок 4.3.2.1 – Совмещённый график приведённого момента сопротивления, его разложения в ряд Фурье и его среднего значения

3. 
   Приведенная статическая характеристика двигателя
   

Приведенная статическая характеристика двигателя определяется как обобщённая сила из уравнения:

---

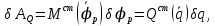
откуда



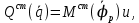
где уравнения статической характеристики электродвигателя постоянного тока независимого возбуждения:



Тогда:




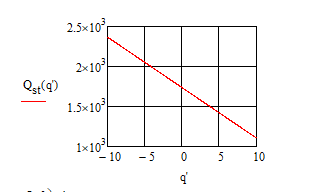
Рисунок 4.3.3.1 – График функции статической характеристики двигателя

4. 
   Возмущающий момент
   

Возмущающий момент – характеристика внутренней виброактивности механизма.

Решения уравнений движения проводятся методом последовательных приближений. Вычисление угловой скорости кривошипа в нулевом приближении – средней скорости вращения выходного звена:



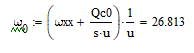
Для разложения функции возмущающего момента в ряд Фурье определим:



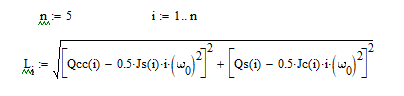
Определение начальных фаз гармоник ряда Фурье:



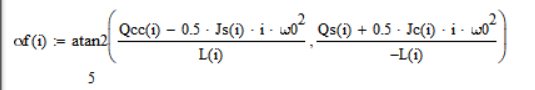
Разложение функции возмущающего момента в ряд Фурье:





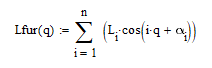
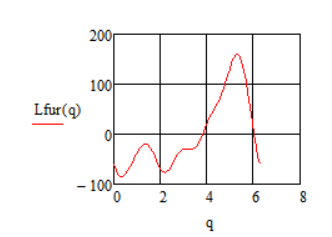
Рисунок 4.3.4.1 – График функции возмущающего момента, разложенного в ряд Фурье

4. 
   Динамические ошибки
   

Вычисление механической постоянной времени машины, необходимой для вычисления динамических ошибок:

1. 
   Динамическая ошибка по углу
   

Разложение функции динамической ошибки по углу в ряд Фурье:



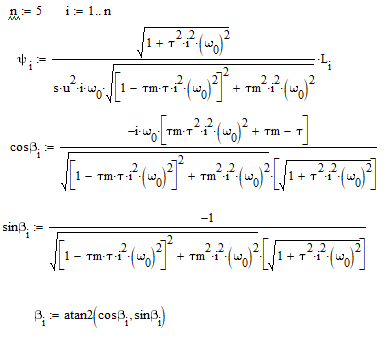
Определение функции динамической ошибки по углу, разложенной в ряд Фурье:

---

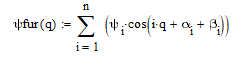
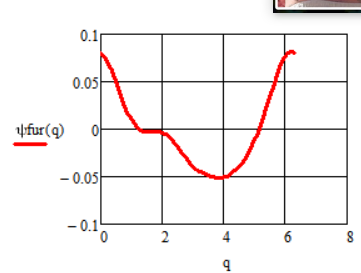
Рисунок 4.4.1.1 – График функции динамической ошибки по углу, разложенной в ряд Фурье

2. 
   Динамическая ошибка по скорости
   

Разложение динамической ошибки по скорости в ряд Фурье:




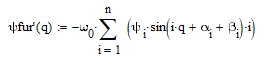
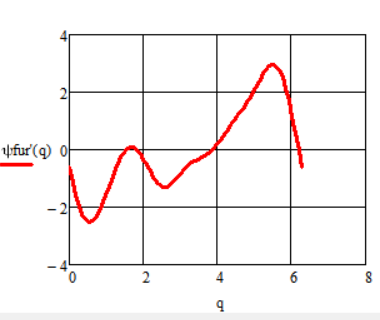
Рисунок 4.4.2.1 – График функции динамической ошибки по скорости, разложенной в ряд Фурье

5. 
   Неравномерность вращения кривошипа
   

В технических требованиях к машине задаются допустимые значения динамических ошибок, оцениваемые коэффициентом неравномерности вращения кривошипа. В данном варианте допустимый коэффициент δ = 0,05. Вычислим максимальную и минимальную динамическую ошибку по скорости:



Коэффициент неравномерности вращения кривошипа:



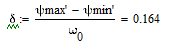
Как видно из расчётов – полученный коэффициент неравномерности вращения кривошипа больше заданного. Машина нуждается в улучшении.

6. 
   Движущий момент
   

Закон изменения движущего момента при учёте механической характеристики двигателя определяется по формуле:



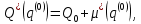
где:

• 
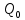  — постоянная часть движущего момента;
  
• 
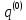  — обобщённая координата в нулевом приближении;
  
• 
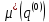  — переменная часть движущего момента.
  

1. 
   Переменная часть движущего момента
   

Произведём разложение функции переменной части движущего момента в ряд Фурье. Определение коэффициентов:



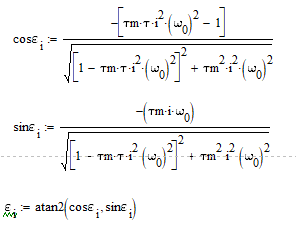
Разложение функции переменной части движущего момента в ряд Фурье:

---

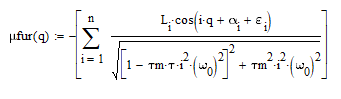
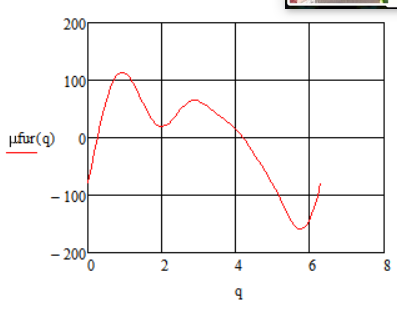
Рисунок4.6.1.1 – График функции переменной части движущего момента, разложенной в ряд Фурье

2. 
   Закон изменения движущего момента
   

Вычисление постоянной части движущего момента:



Определение функции движущего момента:




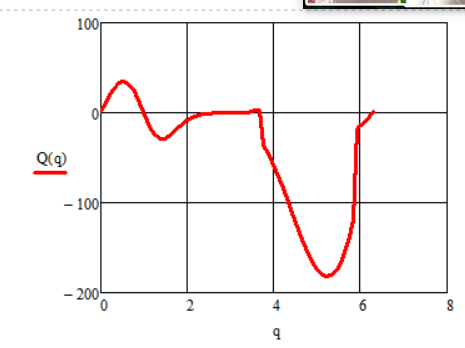
Рисунок 4.6.2.1 – График функции движущего момента

7. 
   Движущий момент в приводе
   

Динамические нагрузки в передаточном механизме являются важной характеристикой установившегося движения. Их можно определить из следующего уравнения:



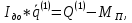
где:

• 
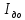  — момент инерции ротора двигателя и передаточного механизма, приведённый к входному звену;
  
• 
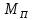  — момент силы в передаточном механизме.
  

Тогда:



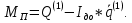
Поскольку:



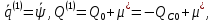
то:

1. 
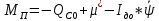
   Определение движущего момента в приводе
   

Вычисление момента инерции ротора двигателя и передаточного механизма, приведённого к входному звену:



Механическая постоянная привода:



Вычисление начальных фаз гармоник ряда Фурье:



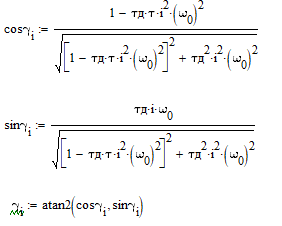
Определение функции движущего момента в приводе:

---

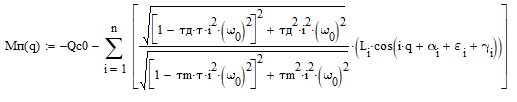
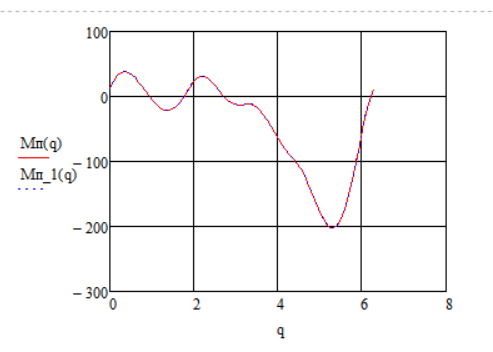
Рисунок 4.7.1.1 – График движущего момента в приводе

2. 
   Условие знакопостоянства движущего момента в приводе
   

Основное требование конструирования привода – знакопостоянство движущего момента в приводе, обеспечивающее отсутствие перекладки зазоров в зубчатых передачах редуктора.

Как видно из графика на рисунке 4.7.1.1, условие нарушается, что ведёт к быстрому износу передач. Следовательно, машина нуждается в улучшении.

8. 
   Улучшение показателей качества машины
   

Улучшить показатели машины можно при помощи установки маховика.

Установка маховика обеспечивает увеличение среднего значения приведённого момента инерции.

Зададим момент инерции маховика, установленного на роторе двигателя:



Тогда приведённый момент инерции будет вычислен, как:




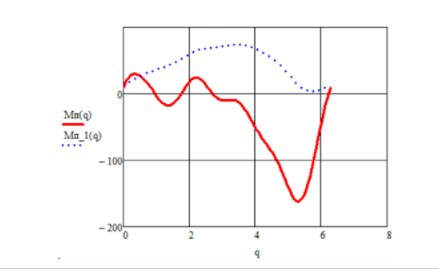
Рисунок 4.8.1 – Полученный график движущего момента в приводе

Как видно из графика, установленного маховика достаточно, чтобы обеспечить условие знакопостоянства движущего момента.

Вычислим коэффициент неравномерности вращения кривошипа:



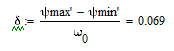
Коэффициент неравномерности вращения всё ещё больше допускаемого значения 0,05. Также можно установить тормоз, но нам удалось добиться знакопостоянства движущего момента, а влияние тормоза на коэффициент неравномерности вращения либо сводится к нулю, либо (при достаточно увеличении усилия на тормозе) вовсе повышает данный коэффициент, что можно видеть в расчётах ниже.

Назначим момент на тормозе:



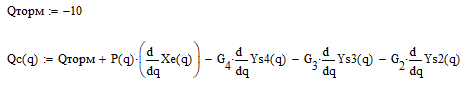
Коэффициент неравномерности вращения при этом:



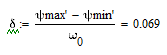
Так же тормоз смещает график движущего момента вверх, что в некоторых случаях может быть полезно, но в нашем – не нужно, так как условие знакопостоянства уже выполняется. При этом тормоз уменьшает КПД машины.

---