Файл: Зубодолбежный станок.docx

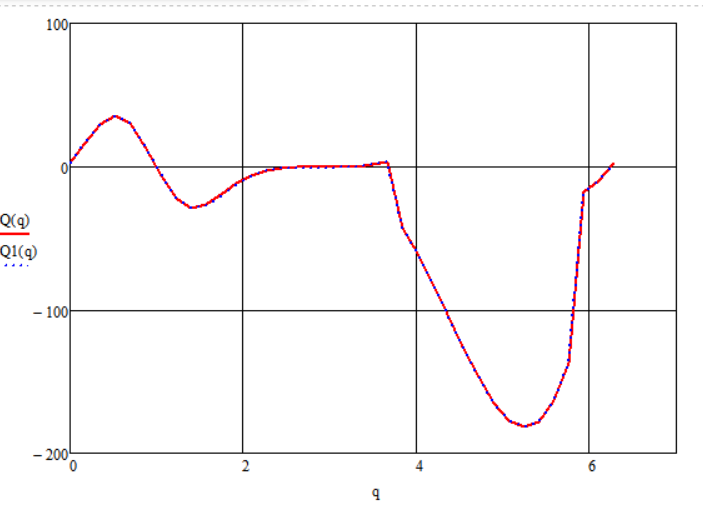
Рисунок 2.3.2.1 - Графики зависимостей Q=Q(q) и Q1=Q1(q)

Как видно из рисунка, графики зависимостей, вычисленных двумя методами, движущего момента от входной координаты совпали, поэтому можно говорить о правильности анализа механизма.

13. 
    Устранение внешней виброактивности механизма
    
    1. 
       Главный вектор сил инерции
       

Мера внешней виброактивности механизма — главный вектор сил инерции.

Определение проекций вектора, а также годограф данного вектора, представлены ниже.





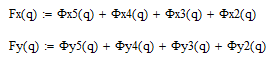
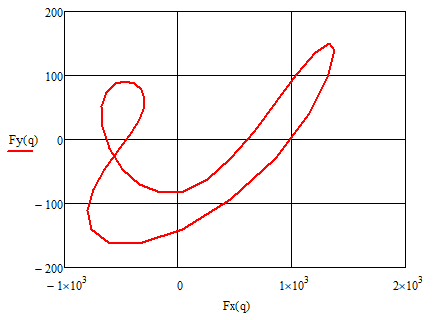
Рисунок 2.4.1.1 – Годограф главного вектора сил инерции

Разложим главный вектор сил инерции в ряд Фурье:

2. 
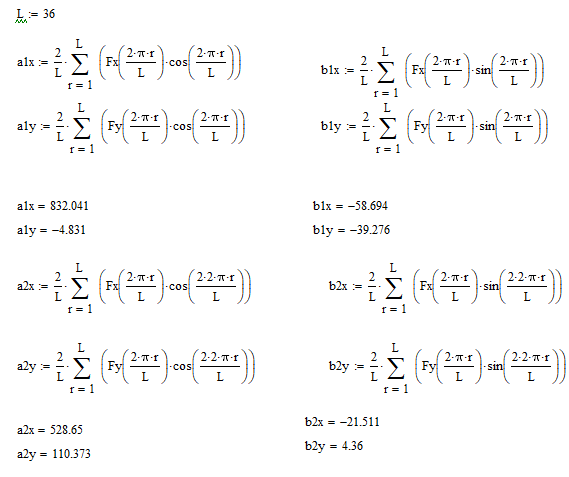
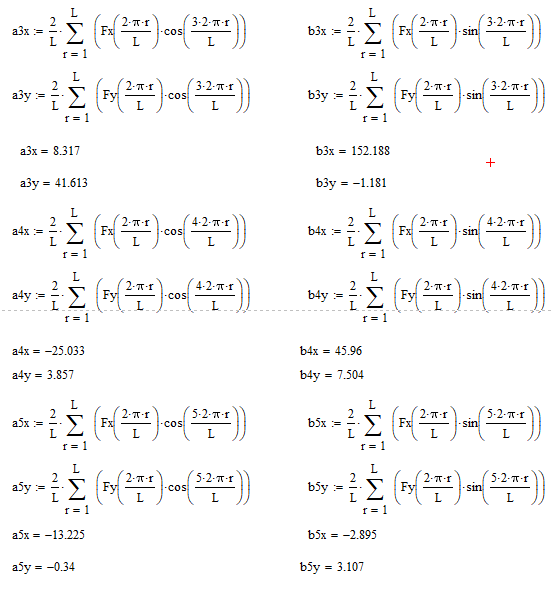
   Эллиптические и круговые гармоники
   

Коэффициенты при первой гармонике имеют большие значения, поэтому нас интересуют только они:



Значения проекций главного вектора сил инерции, разложенные в ряд Фурье с точностью до 1 гармоники:



Эллиптические гармоники могут быть представлены в виде суммы двух круговых гармоник.

Вычислим значения коэффициентов круговых гармоник:



Проекции векторов круговых гармоник:




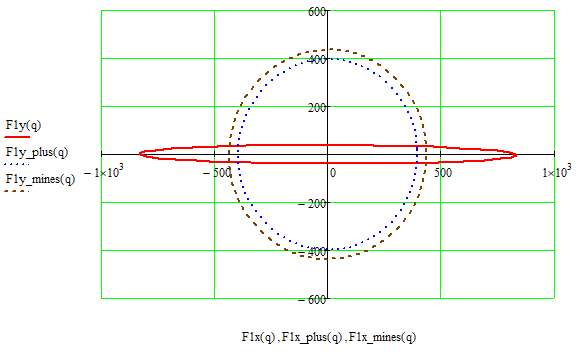
Рисунок 2.4.2.1 – Эллиптическая и круговые гармоники

Модули векторов круговых гармоник:

---

3. 
   Установка противовесов
   

Вычисление начальных углов установки противовесов через синусы и косинусы начальных углов круговых гармоник:



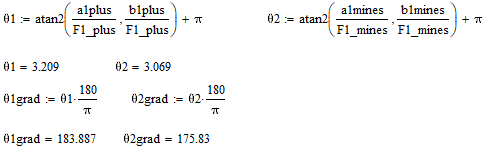
Вычислим массы противовесов:



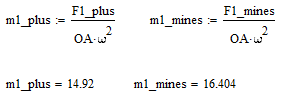
Схема установки противовесов представлена на рисунке 2.4.3.1.


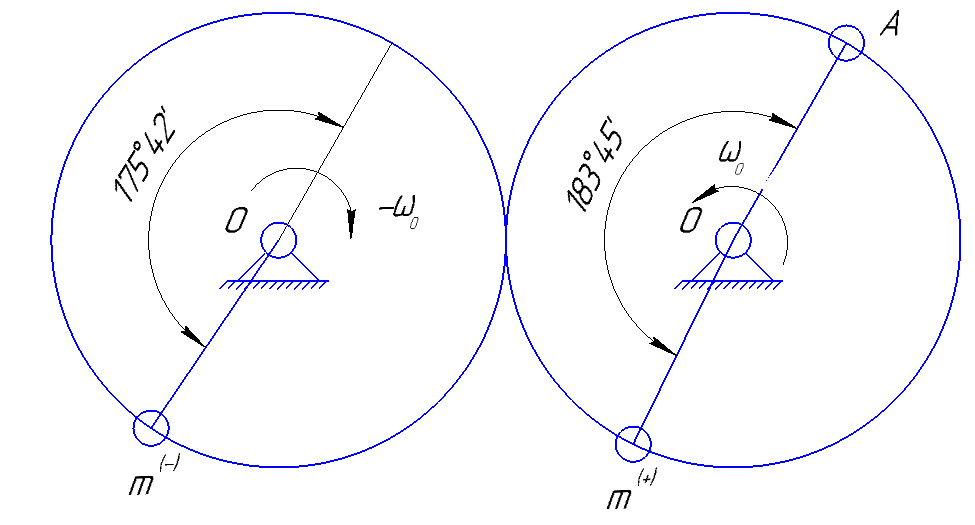
Рисунок 2.4.3.1 – Схема установки противовесов

Определим законы движения противовесов:

Координаты первого противовеса, центр окружности которого совпадает с точкой О, изменяются согласно уравнениям:



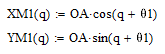
Центр окружности второго противовеса имеет координаты:



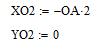
Координаты второго противовеса изменяются согласно уравнениям:



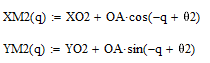
Найдём проекции ускорений противовесов на оси:



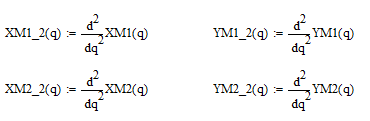
Силы, действующие на противовесы:



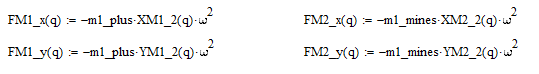
Силы, действующие на корпус машины после установки противовесов:



Совместный график годографов главного вектора сил инерции до и после установки противовесов представлен на рисунке 2.4.3.2.



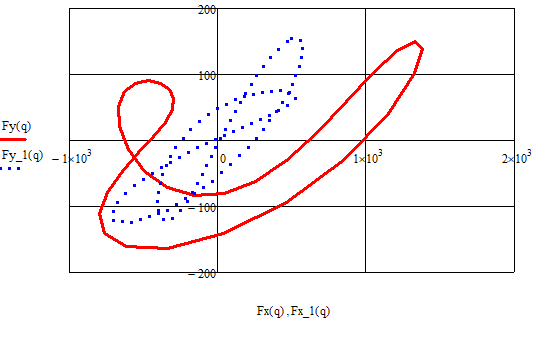
Рисунок 2.4.3.2 – Совмещённый график годографов главного вектора сил инерции

4. 
   Целесообразность установки противовесов
   

В результате установки противовесов годограф главного вектора сил инерции изменился: существенно по оси ОХ, и менее существенно по оси ОУ.

Установка двух противовесов, уменьшающих первую гармонику неуравновешенной силы, не должны обеспечивать полное её устранение.

---

Масса механизма после установки противовесов определяется по формуле:



Результаты уравновешивания приведены в таблице 4.

Таблица 4 – Результаты уравновешивания

	Фх, Н	Фу, Н	m, кг
Без противовесов	2174,05	313,27	37,687
С вращающимися противовесами	1270,9	276,27	69,01
Изменение	-41,5%	-11,8%	+83,1%

Как видно из таблицы, установка противовесов хоть и уменьшила проекции главных векторов сил инерции на оси ОХ и ОУ на 41,5% и на 11,8% соответственно, но увеличила массу механизма в 1,83 раз, что допустимо только в редких случаях, когда нельзя сохранить внутреннюю виброактивность. В нашем случае сделаем вывод, что установка противовесов нецелесообразна.

2. 
   Выбор двигателя
   
   1. 
      Выбор двигателя по каталогу
      

Двигатель выбираем по необходимой (эквивалентной) мощности, т.е. такой мощности, которая требуется для того, чтобы механизм, испытывающий воздействие заданных сил, совершал требуемые движения.

Определим потребляемую двигателем мощность по формуле:



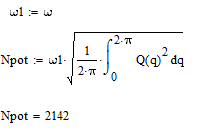
По каталогу выбираем следующий двигатель. Характеристики выбранного электродвигателя постоянного тока независимого возмущения представлены в таблице 5.

Таблица 5 – Характеристики выбранного двигателя

Характеристика	Значение
Типоразмер	2ПН112L
Номинальная мощность, Вт	2200
Номинальная частота вращения ротора, об/мин	1500
Коэффициент перегрузки	2
Номинальный ток, А	11
Номинальное напряжение, В	220
Сопротивление, Ом	0,968
Индуктивность, Гн	0,014
Момент инерции ротора,	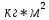0.018

---

2. 
   Проверка условия загрузки двигателя
   

Найдём номинальный момент на двигателе по формуле:



Максимальным моментом на двигателе считаем момент, полученный при максимальной перегрузке (увеличение номинального моменты в 2 раза):



Из графика на рисунке 2.3.2.1 находим максимальное значение движущего момента:



Определяем выполняемость условия:



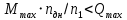
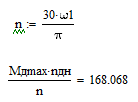
Т. к. 168,068 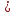178,98, выбранный двигатель удовлетворяет требованиям.

3. 
   Определение параметров двигателя
   

Определим число оборотов в минуту на холостом ходу:



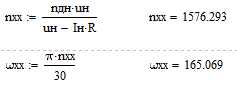
Определим электромагнитную постоянную времени:



Определим крутизну статической характеристики двигателя:

4. 
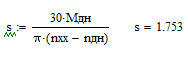
   Выбор редуктора
   

Выбор редуктора осуществляется по передаточному числу:



Был выбран цилиндрический двуступенчатый редуктор, схема которого представлена на рисунке 3.4.1:


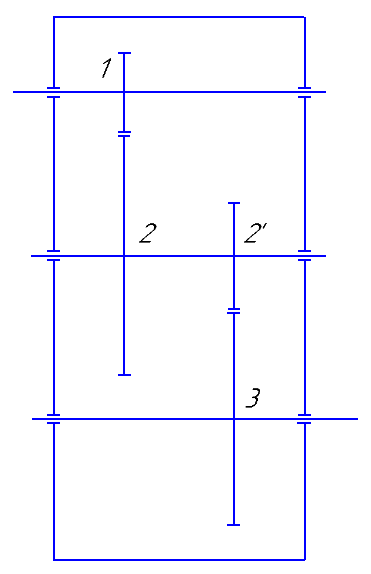
Рисунок 3.4.1 – Схема редуктора

Первая ступень редуктора имеет передаточное отношение 3, вторая – 2.

3. 
   Динамическое исследование машинного агрегата
   
   1. 
      Схема машинного агрегата
      

Машина включает в себя двигатель, передаточный и исполнительный механизма.

Схема машинного агрегата представлена на рисунке 4.1.1.

---

Рисунок 4.1.1 – Схема машинного агрегата

2. 
   Уравнения динамики
   

Движение машины описываются следующими дифференциальными уравнениями движения:





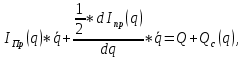
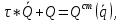
где:

• 
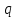  — обобщённая координата;
  
• 
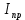  — приведённый момент инерции;
  
• 
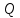  — движущий момент;
  
• 
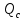  — приведённый момент сил сопротивления;
  
• 
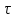  — электромагнитная постоянная времени двигателя;
  
• 
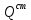  — приведённая статическая характеристика двигателя.
  

3. 
   Определение коэффициентов в системе дифференциальных уравнений
   
   1. 
      Приведённый момент инерции
      

Приведённый момент инерции определяется как коэффициент при половине квадрата обобщённой скорости в выражении кинетической энергии механической системы:


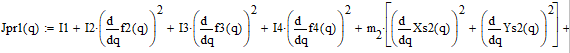
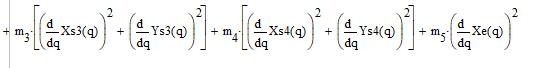
Приведённый момент инерции редуктора:



Приведённый момент инерции механизма с учётом ротора двигателя и редуктора:



Полученная функция с целью упрощения динамических расчётов раскладывается в ряд Фурье с точностью до пяти гармоник:



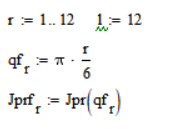
Определим среднее значение:



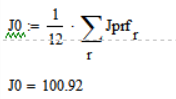
Коэффициент при косинусе в разложении приведённого момента инерции:

---