Добавлен: 30.11.2023
Просмотров: 91
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Средней путевой скоростью называется отношение приращения пути к промежутку времени, в течение которого было пройдено это приращение:
.
Т.к.
, то 
.
Мгновенной скоростью движения называется предел средней скорости при стремлении промежутка времени к 0:
.
Мгновенной путевой скоростью называется предел средней путевой скорости при стремлении промежутка времени к 0:
.
Элементарным промежутком времени dt называется промежуток времени, для которого с заданной наперёд точностью и средняя, и средняя путевая скорость совпадают с соответствующими мгновенными скоростями.
Элементарным перемещением
в произвольном случае назовём перемещение, произошедшее за элементарный промежуток времени dt. Элементарным приращением пути dS в произвольном случае назовём приращение, пройденное за элементарный промежуток времени dt.
Пользуясь языком высшей математики, мы можем сказать, что мгновенная скорость движения или просто скорость движения является первой производной радиус-вектора по времени, а путевая скорость является первой производной по времени путевой координаты.
; 
.
Для того чтобы элементарное перемещение в произвольном случае совпадало с элементарным перемещением для криволинейной траектории нужно, чтобы точности вычисления соотношений
; 
и 
совпадали. Об этом всегда можно условиться. Поэтому мы всегда будем считать, что для элементарного промежутка времени
, следовательно, 
, т.е.
.
Итак,
.
Т.е. модуль скорости движения совпадает с путевой скоростью. Конечное приращение пути по определению
.
По определению ускорением материальной точки называется первая производная по времени скорости движения, т.е. вторая производная по времени радиус-вектора:
.
Итак,
Первое слагаемое связано только со скоростью изменения величины скорости движения. Т.к. эта часть полного ускорения направлена по касательной, то она называется касательным ускорением
.
Второе слагаемое связано только с изменением направления скорости движения. Изобразим два положения материальной точки на траектории, разделённые элементарным приращением пути dS, и соответствующие орты касательной
и 
. Соединим положения с центром кривизны траектории в точке dS.
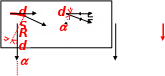
Малый угол da между радиусами совпадает с углом между ортами касательной как острые углы с взаимно перпендикулярными сторонами. Из второго рисунка видно, что
направлен перпендикулярно , т.е. по орту нормали, а его величина
,
следовательно,
.
Угол da связан с элементарным приращением пути dS=R× da, где R – радиус кривизны траектории. Отсюда
. Подставим:
.
Тогда вторая часть полного ускорения имеет вид:
.
Т.к. эта часть ускорения направлена по нормали, то она называется нормальным ускорением.
Сведём все формулы вместе:
4. Относительность скорости движения
Мы уже пользовались понятием системы отсчёта, хотя делать этого не имели права. Из всех атрибутов системы отсчёта был введён только один: начало отсчёта. Другой атрибут – часы, находящиеся в начале отсчёта. Пусть двое часов находились в одной системе отсчёта, а потом «разошлись» по разным. Находясь в одном месте, они были синхронизованы. Как повлияет на их показания относительная скорость? Ответ на это опять зависит от выбора системы постулатов. В механике Ньютона-Галилея «работает» второй постулат Галилея: об абсолютности промежутков времени. Согласно этому постулату, если часы были синхронизованы, то их относительная скорость не влияет на их показания. Вспомним обратное преобразование Галилея для радиус-векторов:
. Возьмём элементарные изменения (дифференциалы) от обеих частей этого равенства.
.
Поделим это равенство на элементарный промежуток времени по часам «основного» наблюдателя, в течение которого произошли элементарные перемещения, равенство останется верным:
.
В соответствие со вторым постулатом Галилея dt=dt', где dt' – промежуток времени по часам «второстепенного» наблюдателя, в течение которого материальная точка переместилась относительно него на
. Значит, можно записать:
.
Это обратное преобразование скорости по Галилею:
.
Прямое преобразование скорости:
5. Система координат
Для количественного описания движения в пространстве необходимо введение координат точки, т.е. совокупности чисел, однозначно определяющей положение материальной точки относительно начала отсчёта. Это возможно только в случае введения третьего атрибута системы отсчёта: системы координат. Теперь можно дать определение системы отсчёта: системой отсчёта называется система координат, в начале которой находится тело отсчёта, снабжённое часами.
В одномерном пространстве для задания «адреса» материальной точки достаточно одного числа, в двумерном пространстве – двух чисел, в трёхмерном – трёх чисел. Способов введения адресации – не один. Например, на плоскости можно задать полярную систему координат (угол, длина радиус-вектора), в пространстве сферическую (длина радиус-вектора, азимутальный угол и угол горизонта). Мы остановимся на подробном рассмотрении системы координат, связанной с разложением радиус-вектора.
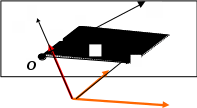
Известно, что любой вектор может быть представлен как сумма трёх векторов, направленных по трём наперёд заданным направлениям, не лежащим в одной плоскости.
.
Здесь
– совокупность ортов, задающих направления. Она называется базисом системы отсчёта. 
– совокупность координат радиус-вектора в этом базисе. Т.к. вектор по трём избранным направлениям раскладывается однозначно
, то однозначно и определение координат точки пространства.
Рассмотрим операцию скалярного умножения двух векторов
и 
(например, радиус-векторов точек пространства А и В):
=
Всего девять слагаемых. Т.к.
, то сумма диагональных элементов совсем проста: 
. Все остальные (перекрёстные члены) кроме произведения координат содержат множители типа
.
Выражение скалярного произведения
можно существенно упростить, если выбрать углы 
. В этом случае говорят, что базис системы координат ортогональный. Только в ортогональном базисе
,
т.к.
и все перекрёстные члены равны 0. Именно в силу простоты записи скалярного произведения ортогональный базис является предпочтительным.
Впервые ортогональную систему координат (СК) ввёл Р. Декарт, и она называется декартовой. Только в декартовой СК
;
докажем это для первой координаты:
,
т.к.
Средней путевой скоростью называется отношение приращения пути к промежутку времени, в течение которого было пройдено это приращение:
.Т.к.
, то .Мгновенной скоростью движения называется предел средней скорости при стремлении промежутка времени к 0:
.Мгновенной путевой скоростью называется предел средней путевой скорости при стремлении промежутка времени к 0:
.Элементарным промежутком времени dt называется промежуток времени, для которого с заданной наперёд точностью и средняя, и средняя путевая скорость совпадают с соответствующими мгновенными скоростями.
Элементарным перемещением
в произвольном случае назовём перемещение, произошедшее за элементарный промежуток времени dt. Элементарным приращением пути dS в произвольном случае назовём приращение, пройденное за элементарный промежуток времени dt.Пользуясь языком высшей математики, мы можем сказать, что мгновенная скорость движения или просто скорость движения является первой производной радиус-вектора по времени, а путевая скорость является первой производной по времени путевой координаты.
; .Для того чтобы элементарное перемещение в произвольном случае совпадало с элементарным перемещением для криволинейной траектории нужно, чтобы точности вычисления соотношений
; и
совпадали. Об этом всегда можно условиться. Поэтому мы всегда будем считать, что для элементарного промежутка времени
, следовательно, , т.е. .Итак,
.Т.е. модуль скорости движения совпадает с путевой скоростью. Конечное приращение пути по определению
.По определению ускорением материальной точки называется первая производная по времени скорости движения, т.е. вторая производная по времени радиус-вектора:
.Итак,
Первое слагаемое связано только со скоростью изменения величины скорости движения. Т.к. эта часть полного ускорения направлена по касательной, то она называется касательным ускорением
.Второе слагаемое связано только с изменением направления скорости движения. Изобразим два положения материальной точки на траектории, разделённые элементарным приращением пути dS, и соответствующие орты касательной
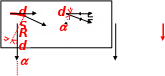
и . Соединим положения с центром кривизны траектории в точке dS. Малый угол da между радиусами совпадает с углом между ортами касательной как острые углы с взаимно перпендикулярными сторонами. Из второго рисунка видно, что
направлен перпендикулярно , т.е. по орту нормали, а его величина
,следовательно,
.Угол da связан с элементарным приращением пути dS=R× da, где R – радиус кривизны траектории. Отсюда
. Подставим: .Тогда вторая часть полного ускорения имеет вид:
.Т.к. эта часть ускорения направлена по нормали, то она называется нормальным ускорением.
Сведём все формулы вместе:
4. Относительность скорости движения
Мы уже пользовались понятием системы отсчёта, хотя делать этого не имели права. Из всех атрибутов системы отсчёта был введён только один: начало отсчёта. Другой атрибут – часы, находящиеся в начале отсчёта. Пусть двое часов находились в одной системе отсчёта, а потом «разошлись» по разным. Находясь в одном месте, они были синхронизованы. Как повлияет на их показания относительная скорость? Ответ на это опять зависит от выбора системы постулатов. В механике Ньютона-Галилея «работает» второй постулат Галилея: об абсолютности промежутков времени. Согласно этому постулату, если часы были синхронизованы, то их относительная скорость не влияет на их показания. Вспомним обратное преобразование Галилея для радиус-векторов:
. Возьмём элементарные изменения (дифференциалы) от обеих частей этого равенства. .Поделим это равенство на элементарный промежуток времени по часам «основного» наблюдателя, в течение которого произошли элементарные перемещения, равенство останется верным:
.
В соответствие со вторым постулатом Галилея dt=dt', где dt' – промежуток времени по часам «второстепенного» наблюдателя, в течение которого материальная точка переместилась относительно него на
. Значит, можно записать: .Это обратное преобразование скорости по Галилею:
.Прямое преобразование скорости:
5. Система координат
Для количественного описания движения в пространстве необходимо введение координат точки, т.е. совокупности чисел, однозначно определяющей положение материальной точки относительно начала отсчёта. Это возможно только в случае введения третьего атрибута системы отсчёта: системы координат. Теперь можно дать определение системы отсчёта: системой отсчёта называется система координат, в начале которой находится тело отсчёта, снабжённое часами.
В одномерном пространстве для задания «адреса» материальной точки достаточно одного числа, в двумерном пространстве – двух чисел, в трёхмерном – трёх чисел. Способов введения адресации – не один. Например, на плоскости можно задать полярную систему координат (угол, длина радиус-вектора), в пространстве сферическую (длина радиус-вектора, азимутальный угол и угол горизонта). Мы остановимся на подробном рассмотрении системы координат, связанной с разложением радиус-вектора.
Известно, что любой вектор может быть представлен как сумма трёх векторов, направленных по трём наперёд заданным направлениям, не лежащим в одной плоскости.
.Здесь
– совокупность ортов, задающих направления. Она называется базисом системы отсчёта. – совокупность координат радиус-вектора в этом базисе. Т.к. вектор по трём избранным направлениям раскладывается однозначно
, то однозначно и определение координат точки пространства.
Рассмотрим операцию скалярного умножения двух векторов
и (например, радиус-векторов точек пространства А и В): =
Всего девять слагаемых. Т.к.
, то сумма диагональных элементов совсем проста: . Все остальные (перекрёстные члены) кроме произведения координат содержат множители типа .Выражение скалярного произведения
можно существенно упростить, если выбрать углы . В этом случае говорят, что базис системы координат ортогональный. Только в ортогональном базисе ,т.к.
и все перекрёстные члены равны 0. Именно в силу простоты записи скалярного произведения ортогональный базис является предпочтительным.Впервые ортогональную систему координат (СК) ввёл Р. Декарт, и она называется декартовой. Только в декартовой СК
-
координаты вектора являются его проекциями на соответствующую ось:
;докажем это для первой координаты:
-
координаты вектора связаны с его модулем соотношением Пифагора:
,т.к.