ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.12.2023
Просмотров: 206
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
данного случая точкой а.
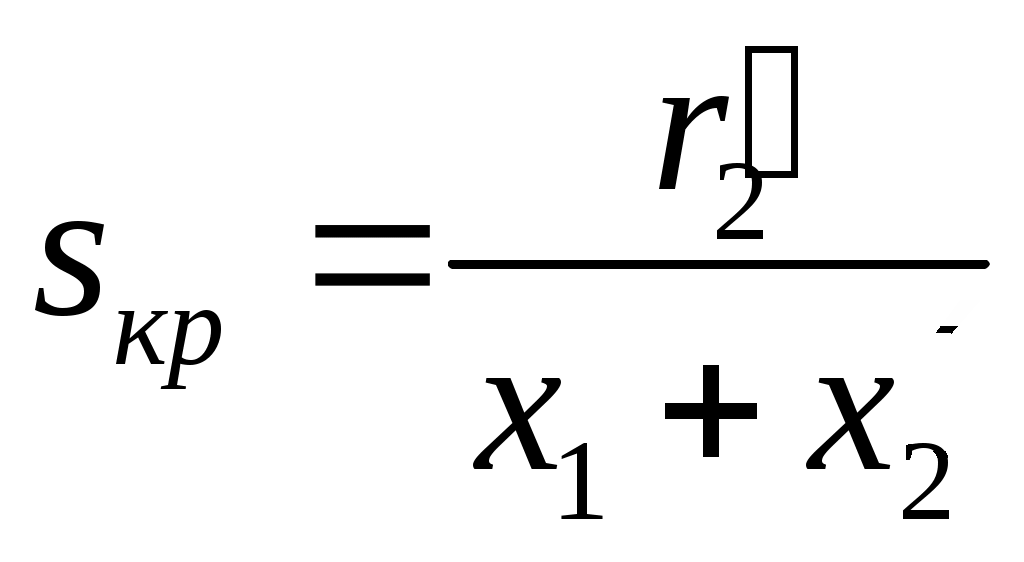 Величина максимального момента определяется значением критического скольжения
Величина максимального момента определяется значением критического скольжения
Подставляя значение sKp в выражение момента (9.8), получаем уравнение максимального вращающего момента
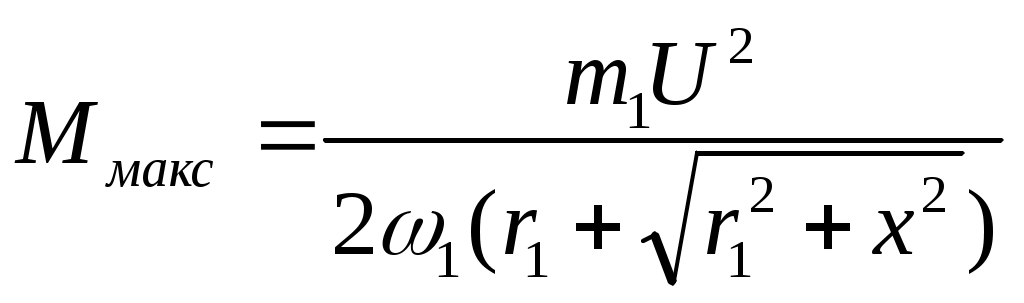
Ввиду того, что в формуле (9.11) r1весьма мало по сравнению с х, то можно записать
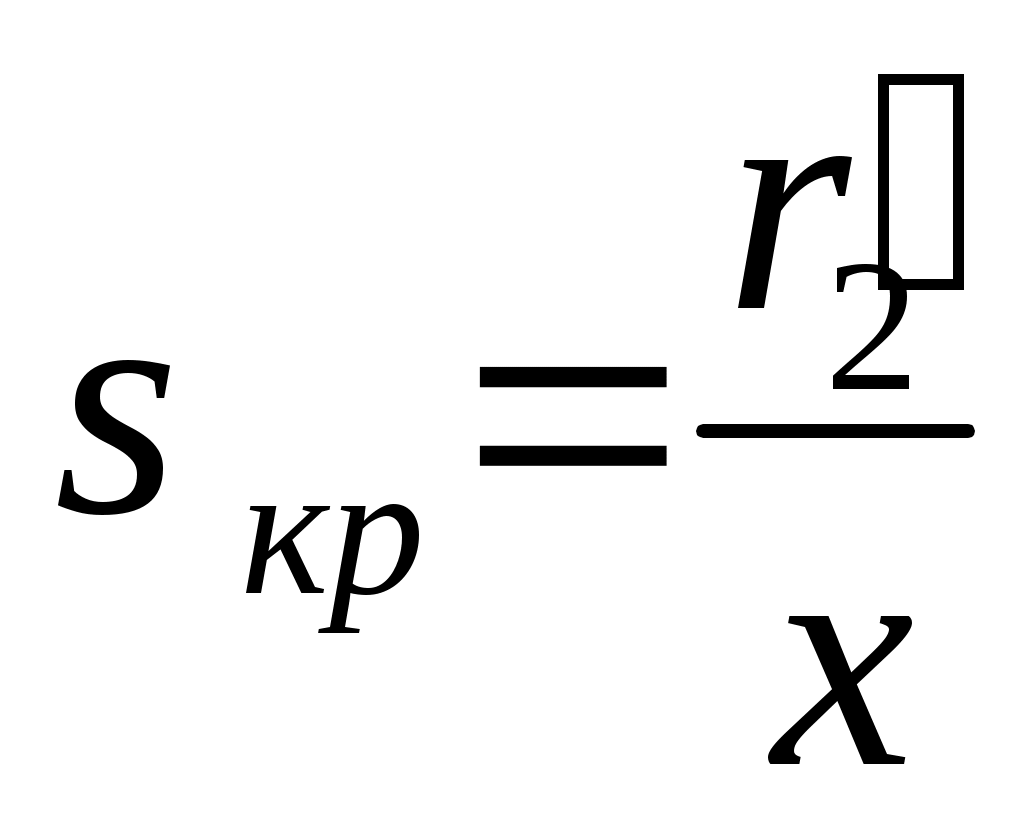
Выражения (9.10) и (9.11) дают возможность сделать выводы:
а) чем больше r’2/x тем большее скольжение будет соответствовать максимальному вращающему моменту;
б) максимальное значение момента не зависит от активного сопротивления ротора r’2;
в) максимальное значение момента пропорционально квадрату напряжения, подводимого к статору (ММАКС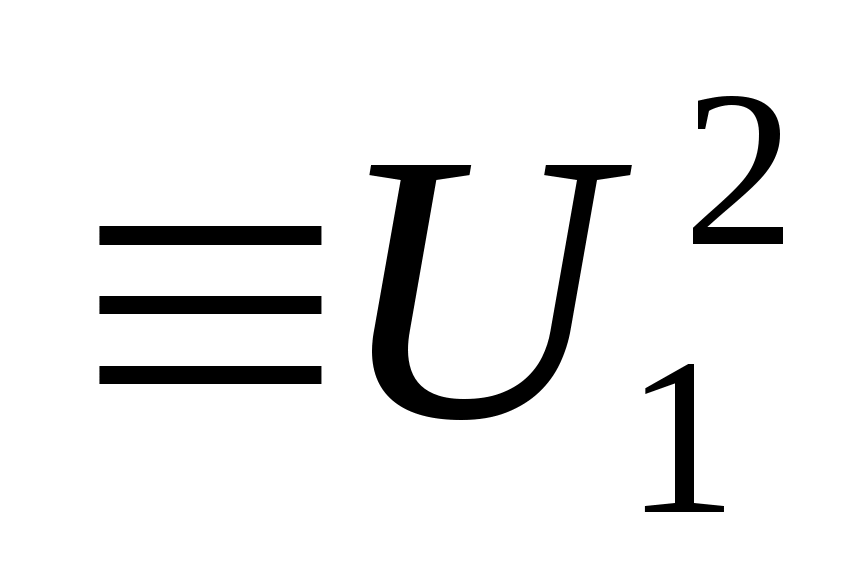 ).
).
Отсюда следует, что если у асинхронного двигателя увеличивать активное сопротивление ротора r2', то максимальный момент, сохраняя свое значение, будет смещаться в сторону больших скольжений (рис. 9.7, б, кривые 2, 3 и 4).
Ток ротора I’2, как известно, вследствие индуктивности обмотки ротора, отстает по фазе от э. д. с. Е2на некоторый угол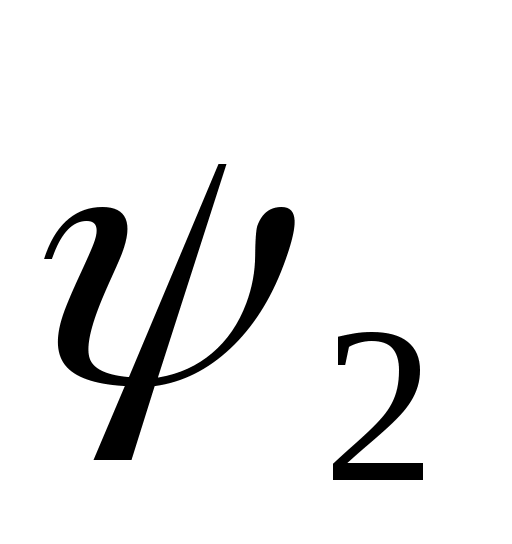 .Из векторной диаграммы (см. рис. 9.5, а) в
.Из векторной диаграммы (см. рис. 9.5, а) в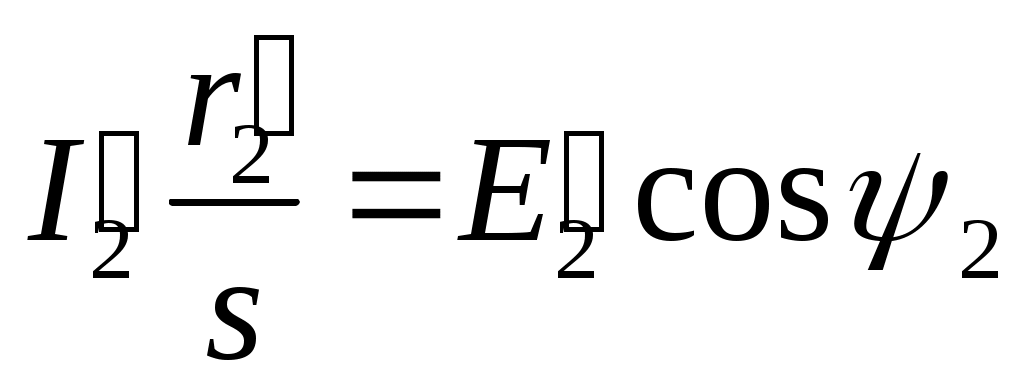 идно, что
идно, что
где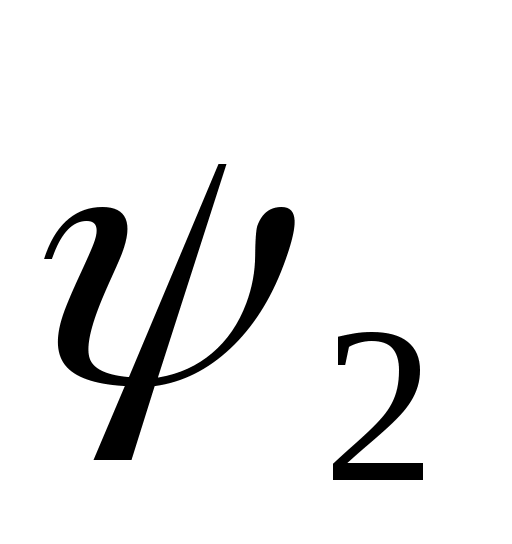 — угол сдвига между Е'2н I2'. Подставляя это значение в формулу (9.7), получим
— угол сдвига между Е'2н I2'. Подставляя это значение в формулу (9.7), получим
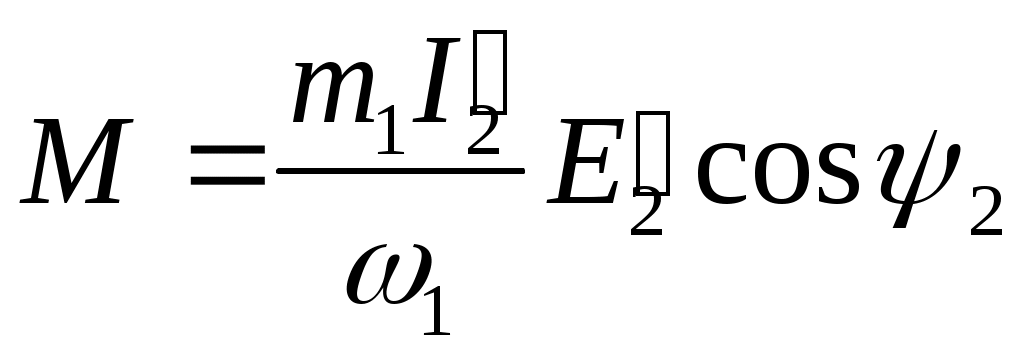
Н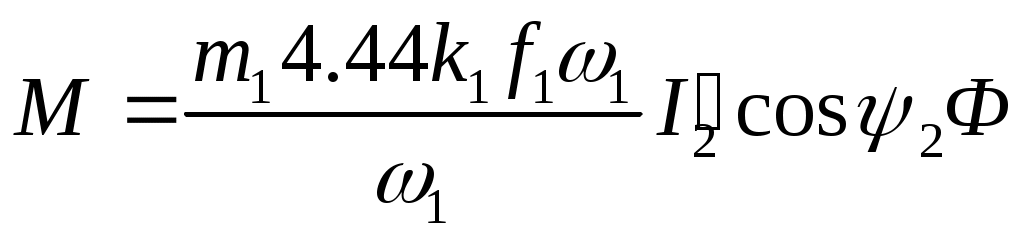 о
о
E’2=E1. Подставив вместо Е’2значение E1 из формулы (9.4), получим
Дробь является постоянной величиной, обозначим ее через kM, тогда
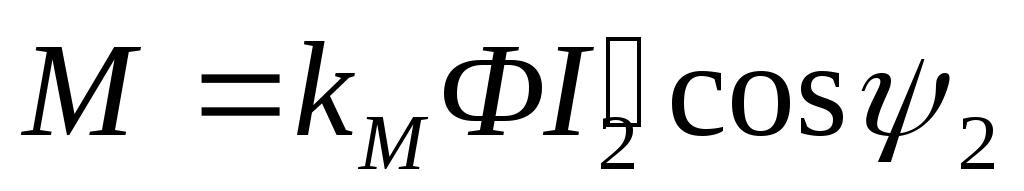
Таким образом, выражение момента асинхронного двигателя отличается от выражения момента машин постоянного тока множителем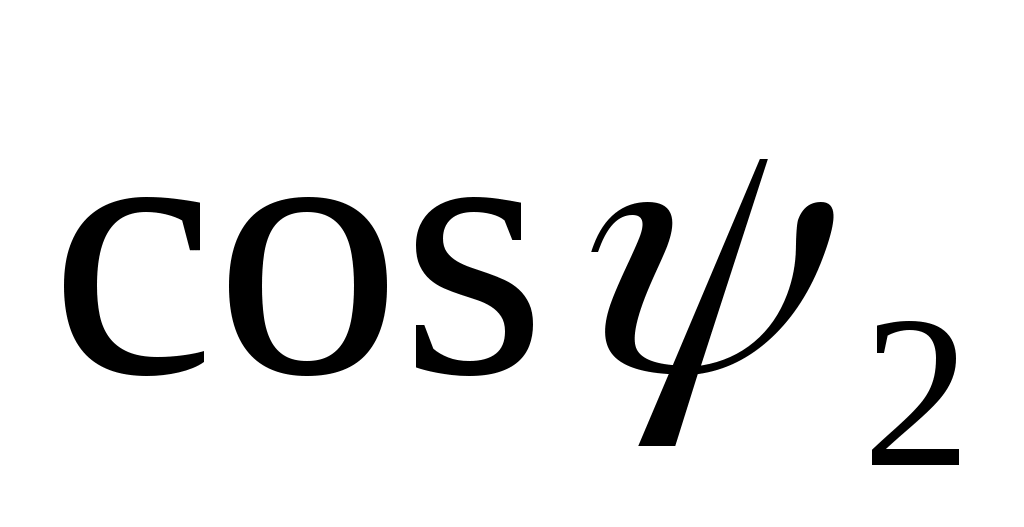 так же, как и формула мощности отличается от формулы мощности машин постоянного тока тем же множителем.
так же, как и формула мощности отличается от формулы мощности машин постоянного тока тем же множителем.
Т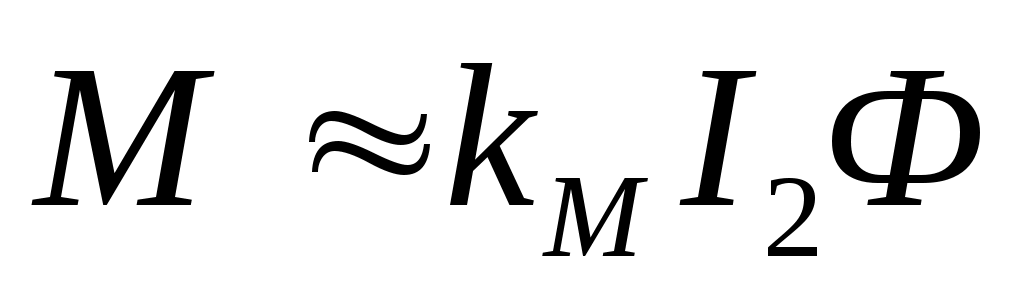 ак как при работе асинхронного двигателя под нагрузкой
ак как при работе асинхронного двигателя под нагрузкой 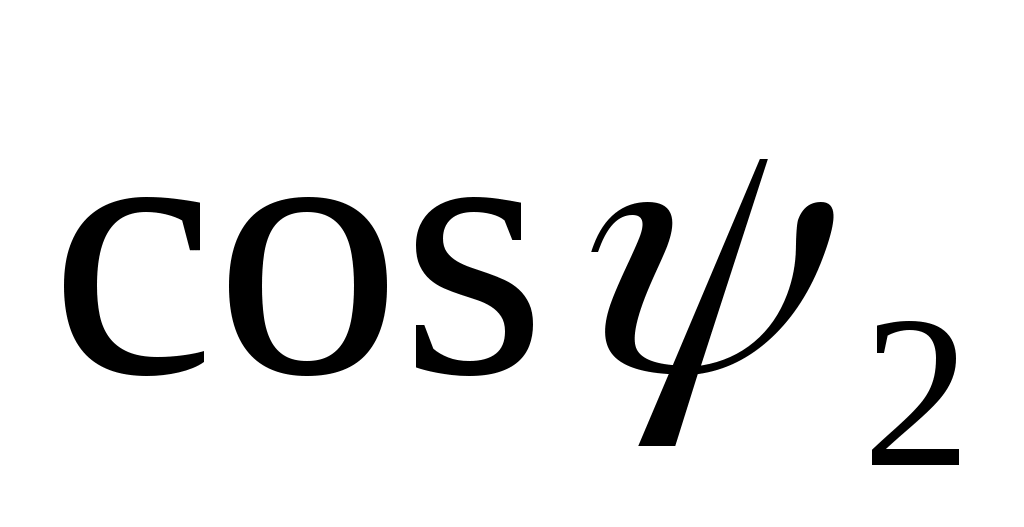 изменяется мало и близок к единице, то приближенно можно написать
изменяется мало и близок к единице, то приближенно можно написать
В начальный момент пуска асинхронного двигателя при неподвижном еще роторе относительная скорость вращающегося магнитного поля и индуктивное сопротивление х будут максимальны, а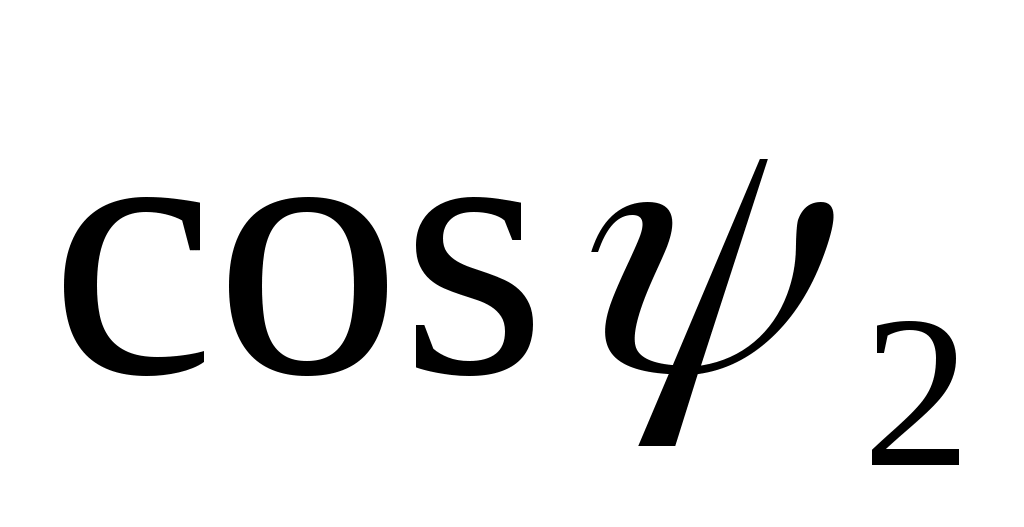 — минимален. Поэтому момент асинхронного двигателя сравнительно невелик, несмотря на большой ток в роторе. Между тем, при пуске двигателя под нагрузкой часто желательно иметь наибольший момент, который может быть получен лишь при условии равенства активного сопротивления вторичной цепи г2 индуктивному сопротивлению двигателя х, т. е. когда r’2/x=1 или r'2=х.
— минимален. Поэтому момент асинхронного двигателя сравнительно невелик, несмотря на большой ток в роторе. Между тем, при пуске двигателя под нагрузкой часто желательно иметь наибольший момент, который может быть получен лишь при условии равенства активного сопротивления вторичной цепи г2 индуктивному сопротивлению двигателя х, т. е. когда r’2/x=1 или r'2=х.
С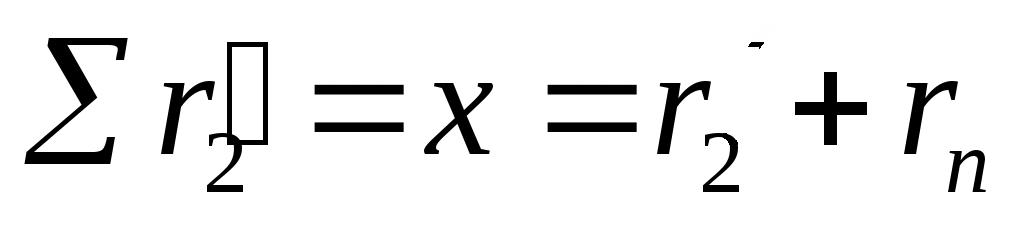 опротивление обмотки ротора г2' меньше индуктивного сопротивления х. У двигателей с контактными кольцами оно может быть повышено введением в цепь ротора пускового реостата. Сопротивление реостата подбирается с таким расчетом, чтобы
опротивление обмотки ротора г2' меньше индуктивного сопротивления х. У двигателей с контактными кольцами оно может быть повышено введением в цепь ротора пускового реостата. Сопротивление реостата подбирается с таким расчетом, чтобы
В момент пуска добавочное сопротивление реостата позволяет получить максимальный момент при
s=l, т. е. получить Мпуск = MМАКС
Кривые зависимости M=f(s) для. разных значений г2' позволяют рассчитать процесс пуска асинхронного двигателя и секции пускового реостата для двигателя с контактными кольцами.
г2' позволяют рассчитать процесс пуска асинхронного двигателя и секции пускового реостата для двигателя с контактными кольцами.
Д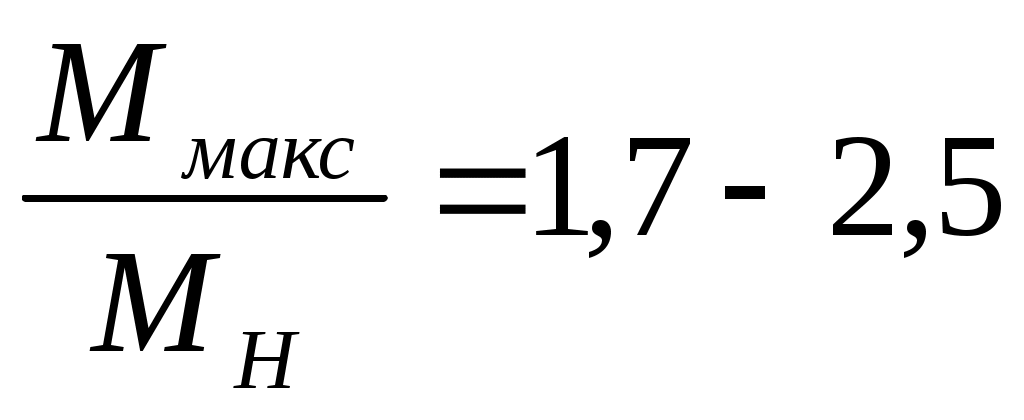 ля устойчивой работы двигателя необходимо, чтобы его максимальный момент был больше номинального, т. е. чтобы двигатель обладал перегрузочной способностью. У асинхронных двигателей единой серии типа А и АО перегрузочная способность
ля устойчивой работы двигателя необходимо, чтобы его максимальный момент был больше номинального, т. е. чтобы двигатель обладал перегрузочной способностью. У асинхронных двигателей единой серии типа А и АО перегрузочная способность
Как отмечалось, максимальный вращающий момент асинхронных двигателей пропорционален квадрату напряжения. Поэтому при снижении напряжения, например, на 30%, т. е. при U1= =0,7UH момент М 'МАКС будет равен всего 0,72ММАКС и может оказаться меньше номинального. В этом случае работа двигателя с номинальной нагрузкой уже невозможна.
§ 9.8. Рабочие характеристики асинхронного двигателя
Рабочие характеристики показывают зависимости: скорости вращения п2, величины тока в статоре I1момента М2, коэффициента мощности , к. п. д.
, к. п. д.  и скольжения s от полезной мощности двигателя Р2 при U1=U1H=const и f=fH=const.
и скольжения s от полезной мощности двигателя Р2 при U1=U1H=const и f=fH=const.
Рабочие характеристики двигателя даны на рис. 9.8. Скоростная характеристика n2=f(Р2) представляет собой кривую, слегка наклоненную к оси абсцисс. Скорость вращения двигателя определяется по формуле n2=n(1—s). В то же время скольжение зависит от отношения потерь в меди Рм2 к развиваемой двигателем электромагнитной мощности;
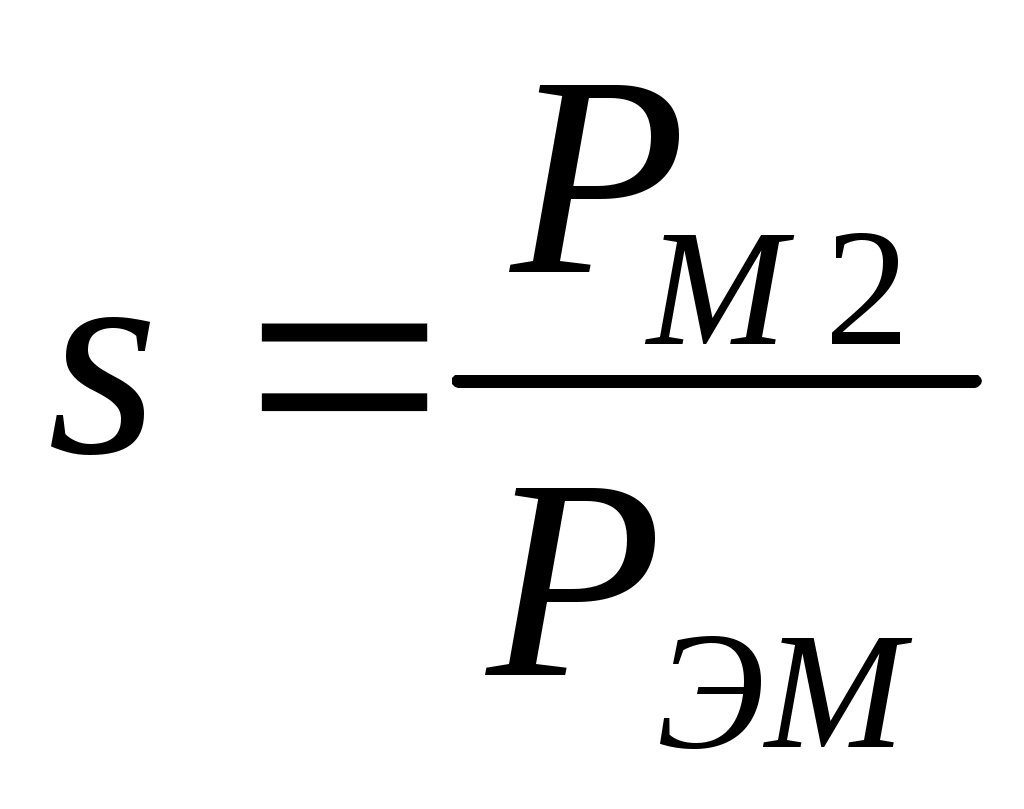
При холостом ходе PM2=0 отсюда s=0 и n2=n1. С увеличением нагрузки отношение PM2/PЭМ растет, но в очень ограниченных пределах.
При увеличении нагрузки от нуля до номинальной скольжение s меняется в пределах 1,5—5%, поэтому и скорость двигателя меняется незначительно. Таким образом, асинхронный двигатель обладает жесткой скоростной характеристикой. - Характеристика момента М2=f(Р2) подобна характеристике синхронного двигателя, так как скорость двигателя в пределах но
минальной нагрузки остается практически постоянной.
К. п. д. двигателя, определяемый зависимостью =f(P2), по мере роста нагрузки увеличивается сначала быстро, затем медленнее и имеет наибольшее значение при нагрузке (0,75
=f(P2), по мере роста нагрузки увеличивается сначала быстро, затем медленнее и имеет наибольшее значение при нагрузке (0,75 0,8) Р2.
0,8) Р2.
Коэффициент мощности cosφ при недогрузке двигателя резко падает вследствие того, что при холостом ходе и малых нагрузках двигатель потребляет реактивный намагничивающий ток, отстающий по фазе от напряжения на угол, близкий к 90°, поэтому всегда следует загружать двигатель в соответствии с его номинальной мощностью. Коэффициент мощности асинхронного двигателя при холостом ходе не превышает 0,2, однако с ростом нагрузки он быстро увеличивается и достигает наибольшего значения (0,8 0,9) при нагрузке, близкой к номинальной.
0,9) при нагрузке, близкой к номинальной.
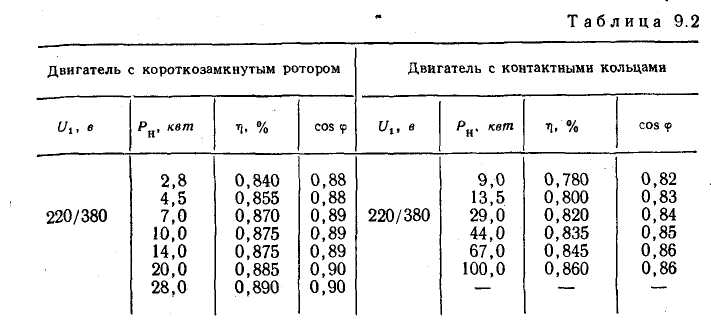
Номинальные значения к.п.д η и коэффициента мощности cosφ различных асинхронных двигателей единой серии приведены в табл.9.2
Потребляемая мощность P1 и ток статора I1 с увеличением полезной мощности возрастают. За счет увеличения потерь (главным образом в меди) возрастание Р1 и I1 при больших нагрузках ускоряется, и кривые загибаются вверх.
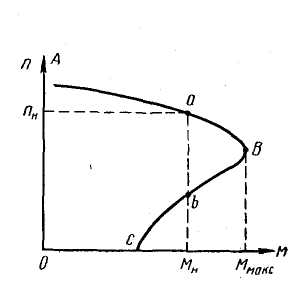
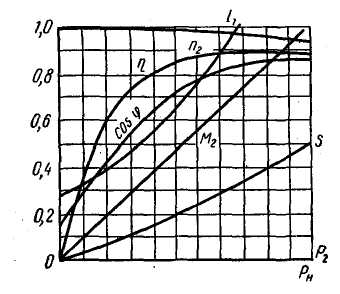
Рис. 9.8. Рабочие характеристики асинхронного двигателя
Рис. 9.9. Механическая характеристика n2=f(M) асинхронного двигателя
Механическая характеристика n2=f(М) является обращенной кривой зависимости момента от скольжения M=f(s) (рис. 9.9).
Подставляя значение sKp в выражение момента (9.8), получаем уравнение максимального вращающего момента
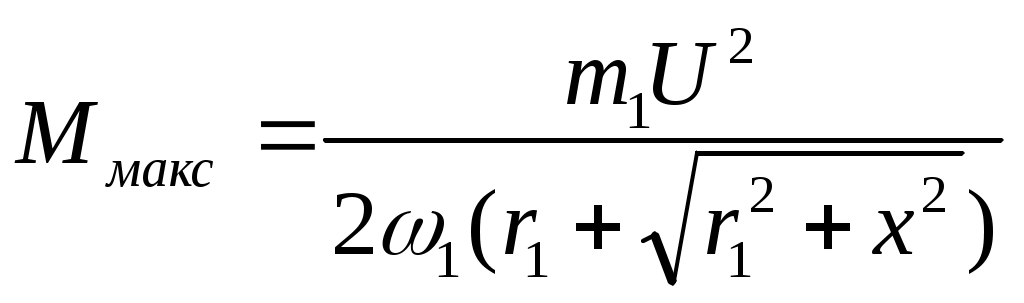
Ввиду того, что в формуле (9.11) r1весьма мало по сравнению с х, то можно записать
Выражения (9.10) и (9.11) дают возможность сделать выводы:
а) чем больше r’2/x тем большее скольжение будет соответствовать максимальному вращающему моменту;
б) максимальное значение момента не зависит от активного сопротивления ротора r’2;
в) максимальное значение момента пропорционально квадрату напряжения, подводимого к статору (ММАКС
Отсюда следует, что если у асинхронного двигателя увеличивать активное сопротивление ротора r2', то максимальный момент, сохраняя свое значение, будет смещаться в сторону больших скольжений (рис. 9.7, б, кривые 2, 3 и 4).
Ток ротора I’2, как известно, вследствие индуктивности обмотки ротора, отстает по фазе от э. д. с. Е2на некоторый угол
где
Н
E’2=E1. Подставив вместо Е’2значение E1 из формулы (9.4), получим
Дробь является постоянной величиной, обозначим ее через kM, тогда
Таким образом, выражение момента асинхронного двигателя отличается от выражения момента машин постоянного тока множителем
Т
В начальный момент пуска асинхронного двигателя при неподвижном еще роторе относительная скорость вращающегося магнитного поля и индуктивное сопротивление х будут максимальны, а
С
В момент пуска добавочное сопротивление реостата позволяет получить максимальный момент при
s=l, т. е. получить Мпуск = MМАКС
Кривые зависимости M=f(s) для. разных значений
Д
Как отмечалось, максимальный вращающий момент асинхронных двигателей пропорционален квадрату напряжения. Поэтому при снижении напряжения, например, на 30%, т. е. при U1= =0,7UH момент М 'МАКС будет равен всего 0,72ММАКС и может оказаться меньше номинального. В этом случае работа двигателя с номинальной нагрузкой уже невозможна.
§ 9.8. Рабочие характеристики асинхронного двигателя
Рабочие характеристики показывают зависимости: скорости вращения п2, величины тока в статоре I1момента М2, коэффициента мощности
Рабочие характеристики двигателя даны на рис. 9.8. Скоростная характеристика n2=f(Р2) представляет собой кривую, слегка наклоненную к оси абсцисс. Скорость вращения двигателя определяется по формуле n2=n(1—s). В то же время скольжение зависит от отношения потерь в меди Рм2 к развиваемой двигателем электромагнитной мощности;
При холостом ходе PM2=0 отсюда s=0 и n2=n1. С увеличением нагрузки отношение PM2/PЭМ растет, но в очень ограниченных пределах.
При увеличении нагрузки от нуля до номинальной скольжение s меняется в пределах 1,5—5%, поэтому и скорость двигателя меняется незначительно. Таким образом, асинхронный двигатель обладает жесткой скоростной характеристикой. - Характеристика момента М2=f(Р2) подобна характеристике синхронного двигателя, так как скорость двигателя в пределах но
минальной нагрузки остается практически постоянной.
К. п. д. двигателя, определяемый зависимостью
Коэффициент мощности cosφ при недогрузке двигателя резко падает вследствие того, что при холостом ходе и малых нагрузках двигатель потребляет реактивный намагничивающий ток, отстающий по фазе от напряжения на угол, близкий к 90°, поэтому всегда следует загружать двигатель в соответствии с его номинальной мощностью. Коэффициент мощности асинхронного двигателя при холостом ходе не превышает 0,2, однако с ростом нагрузки он быстро увеличивается и достигает наибольшего значения (0,8
Номинальные значения к.п.д η и коэффициента мощности cosφ различных асинхронных двигателей единой серии приведены в табл.9.2
Потребляемая мощность P1 и ток статора I1 с увеличением полезной мощности возрастают. За счет увеличения потерь (главным образом в меди) возрастание Р1 и I1 при больших нагрузках ускоряется, и кривые загибаются вверх.


Рис. 9.8. Рабочие характеристики асинхронного двигателя
Рис. 9.9. Механическая характеристика n2=f(M) асинхронного двигателя

Механическая характеристика n2=f(М) является обращенной кривой зависимости момента от скольжения M=f(s) (рис. 9.9).