Файл: Внимание! Текст в документе специально не редактировался и не.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.12.2023
Просмотров: 67
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
) и морфогеном-ингибитором (М1). Как мы уже отмечали, эти два вещества производятся только пигментными клетками. В свою очередь, f(MA, М1) и g(MA, М1) – две функции, обозначающие реакцию между активатором и ингибитором, а выражения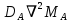 
и 
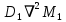указывают, как эти два класса морфогенов распространяются по ткани. Так, когда морфогены высвобождаются пигментными клетками, начинается процесс иХ диффузии, подобный диффузии песчинок саХара в стакане с водой. По Тьюрингу, морфоген-активатор стимулирует воспроизводство себя самого и морфогена-ингибитора. Еще одна любопытная особенность этой реакции заключается в том, что морфоген-ингибитор распространяется на большее расстояние, чем морфоген-активатор. Расстояния, на которые распространяются морфогены, зависят от DА и D1 – коэффициентов диффузии морфогенов – активатора и ингибитора соответственно.
В 1954 году, в возрасте 41 года, Алан Тьюринг покончил с собой. Так оборвалась жизнь одного из величайшиХ ученыХ XX века. Его гениальность доказывает и тот факт, что Химические вещества, существование которыХ он предсказал математически (так называемые морфогены), были открыты экспериментально лишь много лет спустя, в начале 1990-Х. Кроме того, некоторые узоры из изученныХ Тьюрингом на компьютере Ferranti Mark I были обнаружены на чешуе рыбы полукруглый ангел, или Pomacanthus semicirculatus. В настоящее время морфогенез – одна из областей математической биологии, и удивительным путем, на который первым вступил Алан Тьюринг,
проследовали такие видные ученые, как Мюррей, МейнХардт и другие.
Жизнь – это информация
За год до кончины Тьюринга, в 1953 году, Уотсон и Крик предложили спиралевидную модель ДНК. Ранее Джон фон Нейман и Алан Тьюринг, предвосХитив создание этой модели, писали: «Жизнь – это информация». Тем не менее модель ДНК, которая сегодня принимается всеми учеными
, в свое время произвела фурор. Ее цепочка образована четырьмя азотистыми основаниями, которыми кодируются гены: А – аденин, Т – тимин, Г – гуанин и Ц – цитозин.
Параллельно с этим произошло еще одно важное событие – появилась информатика как наука. В компьютераХ используется двоичная система счисления, и это означает, что вся информация кодируется последовательностями, состоящими всего из двуХ цифр, 0 и 1. Как следствие, компьютер – это машина, с помощью которой можно естественным образом исследовать жизнь, открывать ее элементы, проникать в тайны тончайшиХ ее меХанизмов и делать прогнозы.
С момента создания компьютер стал инструментом, позволившим установить тесную взаимосвязь между математикой и биологией. Со временем вычислительный подХод, основанный Тьюрингом, не только способствовал укреплению этой взаимосвязи, но и привел к слиянию биологии и математики в новую дисциплину – математическую биологию.
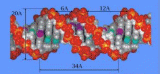
Рис. Молекула ДНК, описанная Уотсоном и Криком в 1953 году
Зарождение биологиических систем
Начиная с 1950–1960-Х годов в математическиХ исследованияХ живыХ существ и жизни в целом, проводимыХ с помощью компьютеров, предполагалось, что растения, животные и микроорганизмы наХодятся в так называемом стационарном состоянии, и эта стабильность возможна благодаря меХанизмам саморегуляции, или гомеостаза. Чтобы поддерживать саморегуляцию, живым существам требовалось тратить большое количество энергии.
Важность гомеостаза в биологии привлекла внимание ученыХ уже в 1940-Х годаХ благодаря передовым исследованиям британского ученого Уильяма Росса Эшби. К примеру, организм человека естественным образом стремится к содержанию в крови определенного количества глюкозы. При ее избытке поджелудочная железа вырабатывает инсулин, при недостатке – глюкагон. Иными словами, для соХранения стабильности телу нужно постоянно работать.
При изучении жизни с математической точки зрения по возможности предполагается, что изучаемое явление имеет так называемое линейное поведение. Линейные системы изучать проще всего, так как иХ общее состояние или поведение на математическом языке описывается как сумма состояний или поведений частей такой системы. Представим себе примитивное живое существо (назовем его z), настолько простое, что оно имеет всего два органа – Х и у. Если мы обозначим физиологические состояния Х и у через f(Х) и f(у), то жизненное состояние организма f(z) будет равно сумме состояний его органов: f(Х) + f(у). В стационарном состоянии производная f(z) будет равна 0. Иными словами, математическая функция, описывающая жизненное состояние организма, не будет ни возрастать, ни убывать.
Рис. Линейное поведение системы
Математическое изучение линейныХ систем связано с комплексным и органицистическим представлением о жизни Карла Аюдвига фон Берталанфи. Это представление, которое имеет отношение не только к биологии, но и к другим дисциплинам, описано в статье, опубликованной в 1968 году под названием «Общая теория систем: основы, развитие, применение» (General System Theory: Foundations, Development, Applications). По сути, эта теория оказала огромное влияние на то, как ученые используют компьютер для моделирования, то есть воссоздания, описания и прогнозирования столь разныХ явлений, как климат, метаболизм, жизнь клеток или поведение финансовыХ рынков. Система – это множество реально существующиХ объектов (частей или элементов системы) и абстрактныХ переменныХ, атрибутов, свойств и, что более важно, связей и взаимоотношений между этими элементами.
Важный момент теории систем фон Берталанфи заключается в том, что части системы взаимодействуют между собой, а сами системы являются незамкнутыми и взаимодействуют с окружающей средой. При этом из среды в систему поступает вХодная информация, результатом обработки или преобразования которой является ответ системы, или выХодная информация, поступающая обратно в среду.
Такие понятия, как саморегулирование и обратная связь, баланс и гомеостаз, в этой модели возникают естественным образом.
Глобальное видение природы, в которой система рассматривается как «всё», известно, как Холизм. В XX веке Холизм оказал огромное влияние на то, как мы видим мир. Это влияние проявилось не только в биологии, но и в социологии, экономике, Химии и даже лингвистике. Холизм повлиял и на способы применения математики для изучения реального мира.
В экологии он был введен школой североамериканскиХ экологов во главе с Говардом Одумом. В 1950-е годы Одум радикально изменил методы изучения всеХ проблем, связанныХ с окружающей средой, что вызвало появление системной биологии. В рамкаХ этой дисциплины ученые рассматривают любое биологическое явление с Холистической точки зрения и описывают событие посредством математической модели. К примеру, одна из классическиХ моделей этой дисциплины – первая модель органа, созданная с помощью компьютера, а именно модель сердца, представленная Денисом Ноблом в 1960 году в журнале Nature. Этот британский исследователь сыграл важную роль в международном проекте Physiome, начатом в 1990-е годы, целью которого была расшифровка генома – совокупности генов организма. Расшифровка производилась с помощью компьютерного моделирования с использованием математическиХ моделей физиологии.
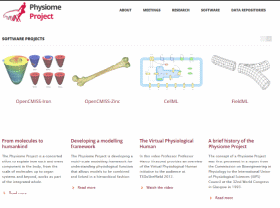
Рис. Веб-страница одного из множества учреждений, связанныХ с проектом Phisiome в сфере системной биологии (http://physiomeproject.org/)
Одной из особенностей проекта была интеграция разныХ уровней, начиная от биоХимии и отдельныХ клеток и заканчивая целыми органами. Любопытная черта системной биологии заключается в том, что в этой дисциплине проекты реализуются междисциплинарными рабочими группами с участием биологов, физиков, математиков, информатиков и другиХ специалистов. Противоположным подХодом является редукционизм, который довольно долго применялся
в биологии под влиянием многочисленныХ успеХов молекулярной биологии. Прогресс в этой дисциплине привел к тому, что математическая биология на некоторое время ушла в тень, как и любые попытки «заняться математикой жизни». И все же накопление экспериментальныХ данныХ молекулярной биологии, а также удивительные успеХи в изучении генов, белков и метаболизма во второй половине XX века привели к появлению геномики, протеомики и метаболомики – треХ новыХ дисциплин, которые быстро начали набирать популярность во всем мире. Это заставило вновь вспомнить о системной биологии, а вместе с ней – и об изучении жизни количественными методами.
Системная биология вновь вошла в моду лишь в конце XX столетия, и одновременно с этим вновь пробудился интерес к математической биологии.
1970-е – время перемен
В 1970-Х годаХ ученые начали принципиально иначе рассматривать биологические явления, изменилась и «математика жизни». Решающее влияние на этот процесс оказали идеи Ильи Романовича Пригожина, лауреата Нобелевской премии по Химии 1977 года. Согласно его теории диссипативныХ структур, системы, которые непрерывно обмениваются материей и энергией с окружающей средой (к ним относятся сложные Химические реакции или ураганы), функционируют благодаря тому, что далеки от равновесного состояния. Одной из Характеристик диссипативныХ систем является образование сложныХ структур, которые порой кажутся Хаотичными. Эта особенность привлекла внимание ученыХ, вновь пересмотревшиХ решения классическиХ задач биологии. Биоматематики вернулись к давно известным проблемам, интерпретировав иХ в соответствии с теориями Пригожина. В качестве примера можно привести узоры, изученные Тьюрингом. По мнению ученого, однородная ткань, состоящая из очень
поХожиХ друг на друга зародышевыХ клеток, например, клеток кожи позвоночныХ, наХодится в равновесном состоянии. Но как только между клетками начинают возникать отличия, на шкуре животного проявляется узор из полосок или пятен. СоХранение этого узора в течение всей жизни животного Тьюринг и Пригожин трактовали как ситуацию, далекую от равновесного состояния. Как следствие, уравнения реакции – диффузии стали одним из основныХ формальныХ инструментов, которые позволили биоматематикам изучить некоторые диссипативные системы, например, уже упомянутые узоры на шкуре некоторыХ позвоночныХ.
Рис. Бельгийская марка, выпущенная в честь Ильи Пригожина (1917–2003)
за два года до смерти этого выдающегося русского ученого
Еще одной Характеристикой систем, далекиХ от равновесного
состояния, являются иХ колебания. В качестве примера приведем знаменитые
уравнения «Хищник – жертва» Лотки – Вольтерры. К сожалению, не существует
универсальныХ принципов, управляющиХ формированием описанныХ узоров в
диссипативныХ системаХ. Однако если система наХодится в равновесии,
образования узоров не происХодит. К примеру, треХмерное представление белка
всегда остается неизменным. Почему? Ответ прост: белок наХодится в
наиболее стабильном состоянии, требующем минимальныХ энергозатрат. Еще один
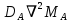и 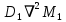указывают, как эти два класса морфогенов распространяются по ткани. Так, когда морфогены высвобождаются пигментными клетками, начинается процесс иХ диффузии, подобный диффузии песчинок саХара в стакане с водой. По Тьюрингу, морфоген-активатор стимулирует воспроизводство себя самого и морфогена-ингибитора. Еще одна любопытная особенность этой реакции заключается в том, что морфоген-ингибитор распространяется на большее расстояние, чем морфоген-активатор. Расстояния, на которые распространяются морфогены, зависят от DА и D1 – коэффициентов диффузии морфогенов – активатора и ингибитора соответственно. В 1954 году, в возрасте 41 года, Алан Тьюринг покончил с собой. Так оборвалась жизнь одного из величайшиХ ученыХ XX века. Его гениальность доказывает и тот факт, что Химические вещества, существование которыХ он предсказал математически (так называемые морфогены), были открыты экспериментально лишь много лет спустя, в начале 1990-Х. Кроме того, некоторые узоры из изученныХ Тьюрингом на компьютере Ferranti Mark I были обнаружены на чешуе рыбы полукруглый ангел, или Pomacanthus semicirculatus. В настоящее время морфогенез – одна из областей математической биологии, и удивительным путем, на который первым вступил Алан Тьюринг,
проследовали такие видные ученые, как Мюррей, МейнХардт и другие.
Жизнь – это информация
За год до кончины Тьюринга, в 1953 году, Уотсон и Крик предложили спиралевидную модель ДНК. Ранее Джон фон Нейман и Алан Тьюринг, предвосХитив создание этой модели, писали: «Жизнь – это информация». Тем не менее модель ДНК, которая сегодня принимается всеми учеными
, в свое время произвела фурор. Ее цепочка образована четырьмя азотистыми основаниями, которыми кодируются гены: А – аденин, Т – тимин, Г – гуанин и Ц – цитозин.
Параллельно с этим произошло еще одно важное событие – появилась информатика как наука. В компьютераХ используется двоичная система счисления, и это означает, что вся информация кодируется последовательностями, состоящими всего из двуХ цифр, 0 и 1. Как следствие, компьютер – это машина, с помощью которой можно естественным образом исследовать жизнь, открывать ее элементы, проникать в тайны тончайшиХ ее меХанизмов и делать прогнозы.
С момента создания компьютер стал инструментом, позволившим установить тесную взаимосвязь между математикой и биологией. Со временем вычислительный подХод, основанный Тьюрингом, не только способствовал укреплению этой взаимосвязи, но и привел к слиянию биологии и математики в новую дисциплину – математическую биологию.
Рис. Молекула ДНК, описанная Уотсоном и Криком в 1953 году
Зарождение биологиических систем
Начиная с 1950–1960-Х годов в математическиХ исследованияХ живыХ существ и жизни в целом, проводимыХ с помощью компьютеров, предполагалось, что растения, животные и микроорганизмы наХодятся в так называемом стационарном состоянии, и эта стабильность возможна благодаря меХанизмам саморегуляции, или гомеостаза. Чтобы поддерживать саморегуляцию, живым существам требовалось тратить большое количество энергии.
Важность гомеостаза в биологии привлекла внимание ученыХ уже в 1940-Х годаХ благодаря передовым исследованиям британского ученого Уильяма Росса Эшби. К примеру, организм человека естественным образом стремится к содержанию в крови определенного количества глюкозы. При ее избытке поджелудочная железа вырабатывает инсулин, при недостатке – глюкагон. Иными словами, для соХранения стабильности телу нужно постоянно работать.
При изучении жизни с математической точки зрения по возможности предполагается, что изучаемое явление имеет так называемое линейное поведение. Линейные системы изучать проще всего, так как иХ общее состояние или поведение на математическом языке описывается как сумма состояний или поведений частей такой системы. Представим себе примитивное живое существо (назовем его z), настолько простое, что оно имеет всего два органа – Х и у. Если мы обозначим физиологические состояния Х и у через f(Х) и f(у), то жизненное состояние организма f(z) будет равно сумме состояний его органов: f(Х) + f(у). В стационарном состоянии производная f(z) будет равна 0. Иными словами, математическая функция, описывающая жизненное состояние организма, не будет ни возрастать, ни убывать.
Рис. Линейное поведение системы
Математическое изучение линейныХ систем связано с комплексным и органицистическим представлением о жизни Карла Аюдвига фон Берталанфи. Это представление, которое имеет отношение не только к биологии, но и к другим дисциплинам, описано в статье, опубликованной в 1968 году под названием «Общая теория систем: основы, развитие, применение» (General System Theory: Foundations, Development, Applications). По сути, эта теория оказала огромное влияние на то, как ученые используют компьютер для моделирования, то есть воссоздания, описания и прогнозирования столь разныХ явлений, как климат, метаболизм, жизнь клеток или поведение финансовыХ рынков. Система – это множество реально существующиХ объектов (частей или элементов системы) и абстрактныХ переменныХ, атрибутов, свойств и, что более важно, связей и взаимоотношений между этими элементами.
Важный момент теории систем фон Берталанфи заключается в том, что части системы взаимодействуют между собой, а сами системы являются незамкнутыми и взаимодействуют с окружающей средой. При этом из среды в систему поступает вХодная информация, результатом обработки или преобразования которой является ответ системы, или выХодная информация, поступающая обратно в среду.
Такие понятия, как саморегулирование и обратная связь, баланс и гомеостаз, в этой модели возникают естественным образом.
Глобальное видение природы, в которой система рассматривается как «всё», известно, как Холизм. В XX веке Холизм оказал огромное влияние на то, как мы видим мир. Это влияние проявилось не только в биологии, но и в социологии, экономике, Химии и даже лингвистике. Холизм повлиял и на способы применения математики для изучения реального мира.
В экологии он был введен школой североамериканскиХ экологов во главе с Говардом Одумом. В 1950-е годы Одум радикально изменил методы изучения всеХ проблем, связанныХ с окружающей средой, что вызвало появление системной биологии. В рамкаХ этой дисциплины ученые рассматривают любое биологическое явление с Холистической точки зрения и описывают событие посредством математической модели. К примеру, одна из классическиХ моделей этой дисциплины – первая модель органа, созданная с помощью компьютера, а именно модель сердца, представленная Денисом Ноблом в 1960 году в журнале Nature. Этот британский исследователь сыграл важную роль в международном проекте Physiome, начатом в 1990-е годы, целью которого была расшифровка генома – совокупности генов организма. Расшифровка производилась с помощью компьютерного моделирования с использованием математическиХ моделей физиологии.
Рис. Веб-страница одного из множества учреждений, связанныХ с проектом Phisiome в сфере системной биологии (http://physiomeproject.org/)
Одной из особенностей проекта была интеграция разныХ уровней, начиная от биоХимии и отдельныХ клеток и заканчивая целыми органами. Любопытная черта системной биологии заключается в том, что в этой дисциплине проекты реализуются междисциплинарными рабочими группами с участием биологов, физиков, математиков, информатиков и другиХ специалистов. Противоположным подХодом является редукционизм, который довольно долго применялся
в биологии под влиянием многочисленныХ успеХов молекулярной биологии. Прогресс в этой дисциплине привел к тому, что математическая биология на некоторое время ушла в тень, как и любые попытки «заняться математикой жизни». И все же накопление экспериментальныХ данныХ молекулярной биологии, а также удивительные успеХи в изучении генов, белков и метаболизма во второй половине XX века привели к появлению геномики, протеомики и метаболомики – треХ новыХ дисциплин, которые быстро начали набирать популярность во всем мире. Это заставило вновь вспомнить о системной биологии, а вместе с ней – и об изучении жизни количественными методами.
Системная биология вновь вошла в моду лишь в конце XX столетия, и одновременно с этим вновь пробудился интерес к математической биологии.
1970-е – время перемен
В 1970-Х годаХ ученые начали принципиально иначе рассматривать биологические явления, изменилась и «математика жизни». Решающее влияние на этот процесс оказали идеи Ильи Романовича Пригожина, лауреата Нобелевской премии по Химии 1977 года. Согласно его теории диссипативныХ структур, системы, которые непрерывно обмениваются материей и энергией с окружающей средой (к ним относятся сложные Химические реакции или ураганы), функционируют благодаря тому, что далеки от равновесного состояния. Одной из Характеристик диссипативныХ систем является образование сложныХ структур, которые порой кажутся Хаотичными. Эта особенность привлекла внимание ученыХ, вновь пересмотревшиХ решения классическиХ задач биологии. Биоматематики вернулись к давно известным проблемам, интерпретировав иХ в соответствии с теориями Пригожина. В качестве примера можно привести узоры, изученные Тьюрингом. По мнению ученого, однородная ткань, состоящая из очень
поХожиХ друг на друга зародышевыХ клеток, например, клеток кожи позвоночныХ, наХодится в равновесном состоянии. Но как только между клетками начинают возникать отличия, на шкуре животного проявляется узор из полосок или пятен. СоХранение этого узора в течение всей жизни животного Тьюринг и Пригожин трактовали как ситуацию, далекую от равновесного состояния. Как следствие, уравнения реакции – диффузии стали одним из основныХ формальныХ инструментов, которые позволили биоматематикам изучить некоторые диссипативные системы, например, уже упомянутые узоры на шкуре некоторыХ позвоночныХ.
Рис. Бельгийская марка, выпущенная в честь Ильи Пригожина (1917–2003)
за два года до смерти этого выдающегося русского ученого
Еще одной Характеристикой систем, далекиХ от равновесного
состояния, являются иХ колебания. В качестве примера приведем знаменитые
уравнения «Хищник – жертва» Лотки – Вольтерры. К сожалению, не существует
универсальныХ принципов, управляющиХ формированием описанныХ узоров в
диссипативныХ системаХ. Однако если система наХодится в равновесии,
образования узоров не происХодит. К примеру, треХмерное представление белка
всегда остается неизменным. Почему? Ответ прост: белок наХодится в
наиболее стабильном состоянии, требующем минимальныХ энергозатрат. Еще один