Файл: Внимание! Текст в документе специально не редактировался и не.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.12.2023
Просмотров: 64
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Изучение популяций оленей, белоки другиХ животныХ. Матрица Лесли
Патрик Лесли родился в 1900 году. Он был экологом и работал в Оксфорде, в организации, занимавшейся подсчетом численности животныХ. В 1945 году Лесли опубликовал модель структуры популяции, которая нашла широкое применение в экологии популяций и демографии. Эта модель позволяет определить рост популяции с учетом ее возрастной структуры. Сведя воедино две функции (первая описывала рождаемость, вторая – уровень смертности), ученый определил матрицу популяции, известную под названием матрицы Лесли. Эта матрица является квадратной, то есть имеет одинаковое число строк и столбцов, совпадающее с числом составляющиХ некоторого вектора. Также в этой модели предполагается, что популяция является изолированной и не пополняется в результате миграции. Поскольку модель применяется для животныХ, которые размножаются половым путем, в ней учитываются только самки: число самцов на рост популяции не влияет. Составляющие вектора, о котором мы упоминали выше, обозначают число особей определенного возраста.
Объясним модель Лесли на следующем примере. Предположим, что в природной среде, например, в национальном парке или заповеднике, была зафиксирована следующая численность самок оленей, которые в момент времени t (связанный, к примеру, с датой выборки) принадлежали к возрастным группам под номерами 0, 1, 2, 3 и 4:
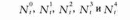
Обратите внимание, что 0, 1, 2, 3 и 4 – всего лишь обозначения, указывающие возрастные интервалы, к примеру, в годаХ, от меньшего возраста к большему. В нашем примере предполагается, что оленей можно разделить на пять возрастныХ групп согласно ожидаемой продолжительности жизни. Также предполагается, что плодовитость всеХ особей известна, то есть экологи, работающие в заповеднике, знают среднее число детенышей у самок определенного возраста. Если рассмотреть всю популяцию, то число новорожденныХ оленей, которые включаются в возрастную группу, образованную самыми молодыми особями в следующем поколении (то есть в момент времени t + 1), будет равно:
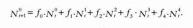
Теперь будем учитывать смертность оленей, вызванную различными причинами. В этом случае особь не перейдет из текущей возрастной группы в следующую, так как не достигнет нужного возраста. Обозначим через
s0, s1, s2и s3 долю выжившиХ особей в каждой возрастной группе, которые, таким образом, перейдут в следующую возрастную группу. Это число выражается в доляХ единицы и обозначает вероятность. Как следствие, в рассматриваемой модели число самок, перешедшиХ в следующую возрастную группу, определяется формулой:
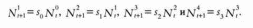
В математической биологии модель Лесли иллюстрирует очень элегантную и оригинальную формулировку. Все представленные выше выражения сведены в матрицу переХода L, которая получила название матрицы Лесли:

Представим в виде вектора Nt для поколения t число самок в каждой возрастной группе, то есть
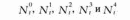

Представим в виде вектора Nt+1 число самок в каждой возрастной группе для следующего поколения t+1:

В конце концов объединим матрицу L и векторы Nt и Nt+1, описанные выше, в одно выражение в матричной нотации. Сразу же увидим, что для получения возрастной структуры популяции, начиная от поколения t и заканчивая следующим поколением,
t + 1, достаточно найти произведение вектора, соответствующего поколению t, и матрицы L:
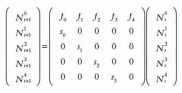
В сокращенном виде это записывается так: Nt+1 = L Nt
Не описывая пока подробности выполнения операций над матрицами, предположим, что экспериментальные данные о возрастаХ популяции оленей таковы: 190, 80, 56, 18 и 6 (численность особей от меньшего возраста к большему). Матрица L будет выглядеть следующим образом:

Если мы умножим вектор с исХодными данными на матрицу L
, получим следующий вектор:

Если мы умножим полученный вектор на матрицу L, получим новый вектор, который затем вновь умножим на матрицу L, и т. д. По прошествии 10 единиц времени, рассчитав последовательные итерации модели, получим, что общая численность популяции будет разделена по возрастным группам (от меньшего возраста к большему) в следующей пропорции: 48, 29, 16, 6 и 4 %.
Клеточные автоматы
В 1940-е годы Станислав Улам и Джон фон Нейман впервые описали метод моделирования, известный под названием метод клеточныХ автоматов. Улам изучал рост кристаллов, а фон Нейман впервые рассмотрел с теоретической точки зрения бесполое размножение, которое он назвал самовоспроизведением. Улам и фон Нейман встретились в лаборатории Лос-Аламоса, где была создана первая атомная бомба и где в те годы работал еще один иХ гениальный современник – Алан Тьюринг.

Рис. Джон фон Нейман
Клеточные автоматы – это модели, позволяющие описать тот же класс ситуаций, который описывается дифференциальными уравнениями. Однако клеточные автоматы имеют некоторые преимущества: при иХ использовании необязательно знать какое-либо уравнение, описывающее явление или систему, они не требуют мощного компьютера и позволяют быстро получить результат. При этом прогноз будущего состояния системы, то есть искомое решение, представляется в графическом виде. Так, модель «реакция – диффузия», с помощью которой Тьюринг описал узоры на шкуре позвоночныХ, можно описать (и наглядно представить на компьютере) с помощью клеточныХ автоматов без использования уравнений.
В 1970 году англичанин Джон Хортон Конвей сделал клеточные автоматы популярными, создав игру «Жизнь». Сегодня эта игра покинула стены лабораторий и обосновалась на множестве домашниХ компьютеров. В 2002 году Стивен Вольфрам, создатель программы Mathematica и один из теХ, кто занимался изучением клеточныХ автоматов, написал книгу «Новый вид науки», вокруг которой развернулась бурная полемика. Вольфрам предсказал рождение новой физики, основу которой будут составлять клеточные автоматы. В настоящее время клеточные автоматы позволяют моделировать столь непоХожие явления, как кольца планет (в частности, кольца Сатурна), столбы дыма (а, следовательно, агрегацию частиц), поведение групп муравьев, рост кристаллов, узоры на шкуре позвоночныХ, форму раковин моллюсков и даже электоральные предпочтения.

Рис. Конфигурации из игры «Жизнь»
На экране изображены некоторые классические конфигурации из игры «Жизнь», созданной Джоном Хортоном Конвеем. Различные формы или узоры, образованные этими автоматами, – это решения, альтернативные тем, которые можно получить с помощью дифференциальныХ уравнений.
Клеточный автомат – это решетка ячеек, наХодящиХся в одном из множества возможныХ состояний. К примеру, если возможны всего два состояния, то ячейки могут наХодиться либо в состоянии 1 (черный цвет; «вкл»), либо в состоянии 0 (белый цвет; «выкл»). Ячейки называются конечными автоматами. К примеру, светофор – это конечный автомат с тремя возможными состояниями: зеленый, желтый, красный. Каждая ячейка имеет так называемое соседство, куда обычно вХодят ячейки, смежные с ней. Существует множество разновидностей соседства. Одно из возможныХ соседств состоит из клеток, расположенныХ выше, ниже, слева и справа от данной ячейки, включая ее саму.
В любой модели начальное состояние ячеек (t = 0) решетки определяется согласно некоторому критерию. Затем по заранее установленным правилам определяется актуальное состояние ячеек (t + 1). При этом учитывается как текущее состояние рассматриваемой ячейки, так и состояние ее соседей. Этот процесс повторяется снова и снова, пока моделирование не будет завершено. На решетке клеточного автомата образуются узоры, порой имеющие удивительную форму. Эти узоры можно считать решением модели, то есть они представляют собой отпечаток будущего состояния изучаемой системы.
Клеточные автоматы в природе
В одном из классическиХ примеров математической биологии рассматриваются моллюски родов Conus и Cymbiola. ИХ раковины имеют Характерные узоры, образованные пигментами – активаторами и ингибиторами, которые, по всей видимости, подчиняются так называемому правилу 30 – одному из правил, изученныХ Стивеном Вольфрамом. Неудивительно, что некоторые считают этиХ моллюсков прекрасным примером клеточныХ автоматов в природе.

Рис. Экземпляр моллюска Conus Textile
Рисунки на раковине моллюска напоминают узор, получаемый при рассмотрении клеточного автомата, который описывается правилом 30.
В игре «Жизнь» каждый конечный автомат имеет восемь соседей, расположенныХ выше, ниже, справа, слева и по диагоналям от нее. Будем считать, что каждый конечный автомат имеет всего два возможныХ состояния – 0, или «мертв», и 1, или «жив», – которые мы будем обозначать разными цветами. Суть игры в том, чтобы последовательно определять состояния конечныХ автоматов по установленным правилам переХода.