Файл: В. Н. Коваленко надежность устройств железнодорожной автоматики, телемеханики и связи.doc

Частотой отказов называется отношение числа отказов изделий в единицу времени к первоначальному числу испытываемых изделий при условии, что все вышедшие из строя изделия не восстанавливаются. Статистическая оценка частоты отказов определяется по выражению

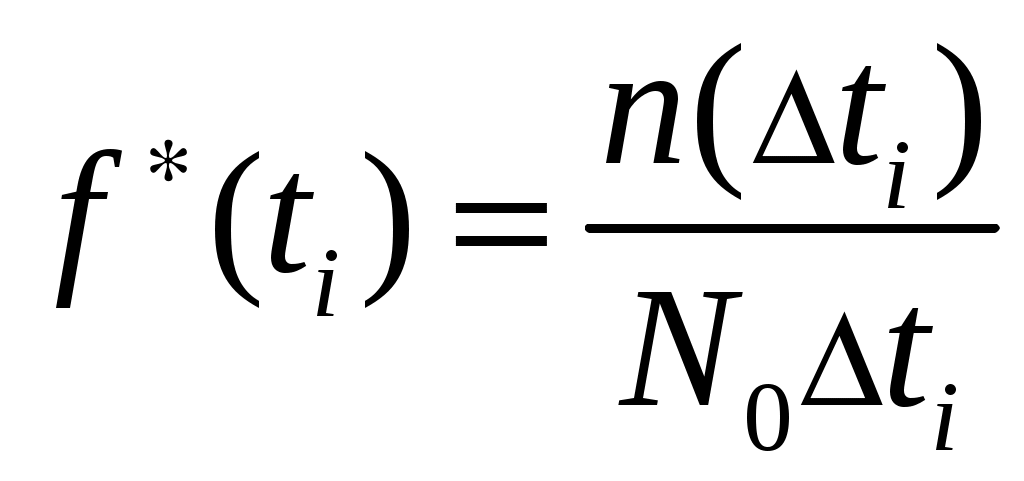, (1.6)

где - число отказавших изделий в интервале времени от - до + ;

- число изделий, поставленных на испытания;

- интервал времени, для которого определяется частота.

Частота отказов есть плотность вероятности (или закон распределения) времени работы изделия до первого отказа.

Тогда справедливы выражения

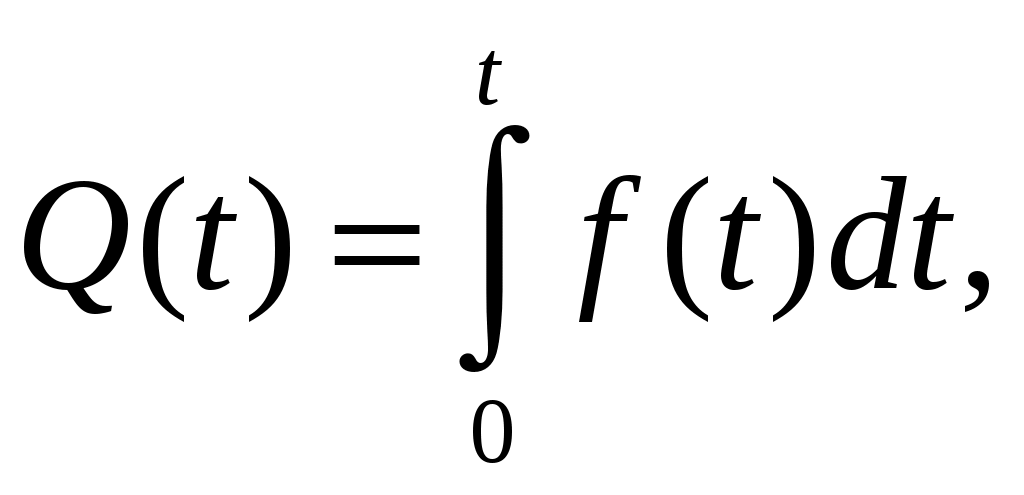
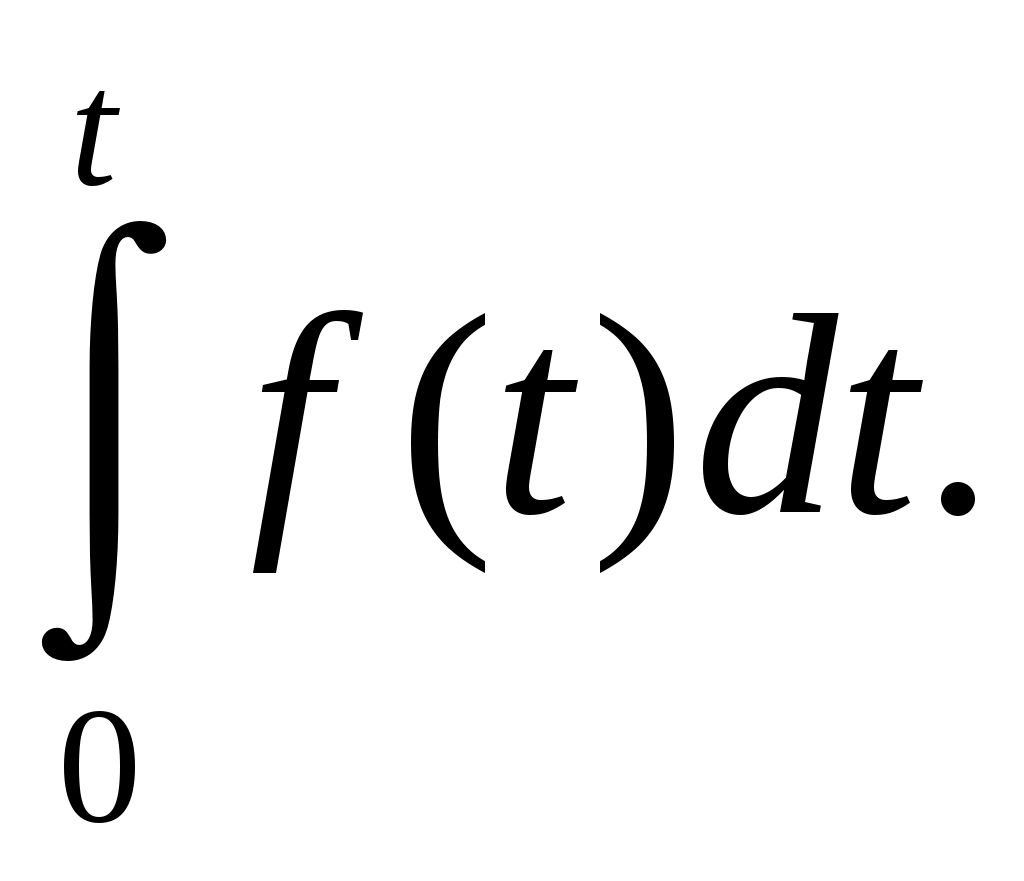(1.7)

Интенсивностью отказов называется отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный интервал времени. Поэтому согласно определению статистическая оценка интенсивности отказов определяется по выражению

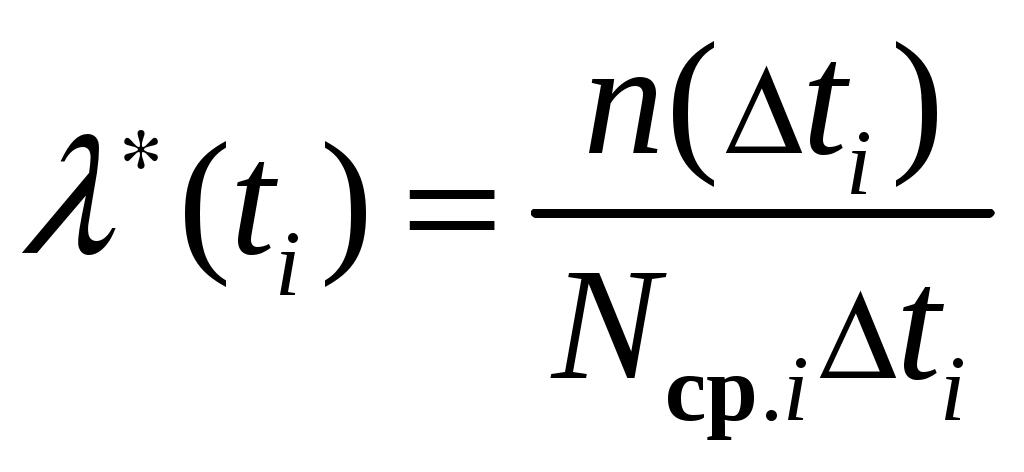, (1.8)

где - среднее число исправно работающих изделий в интервале времени ;

- число изделий, исправно работающих в начале интервала времени

---

;

- число изделий, исправно работающих в конце интервала времени .

Вероятностная оценка интенсивности отказов может быть определена из выражения

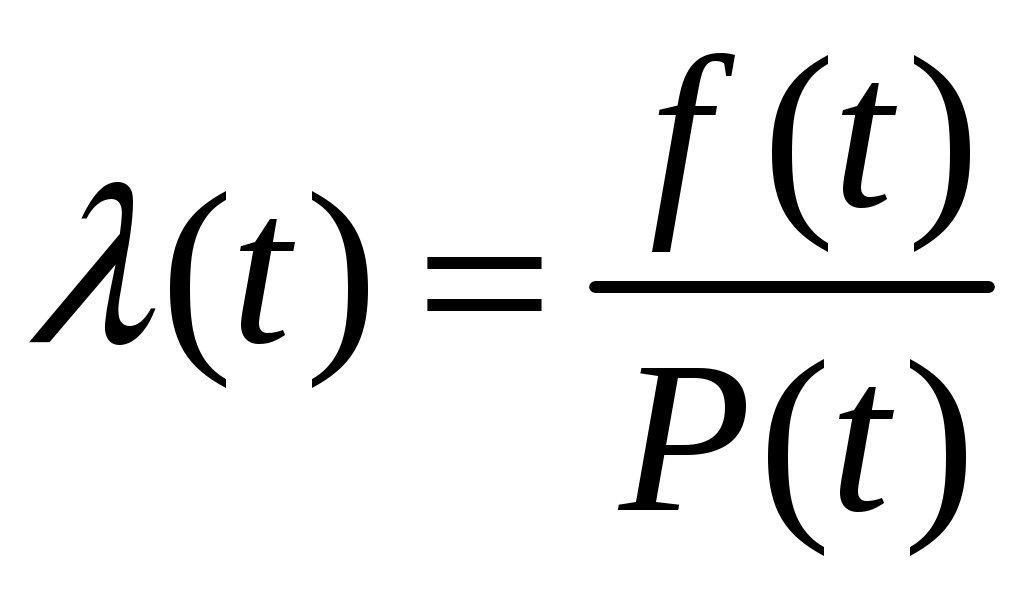(1.9)

Вероятность безотказной работы может быть определена по известной зависимости от времени по выражению

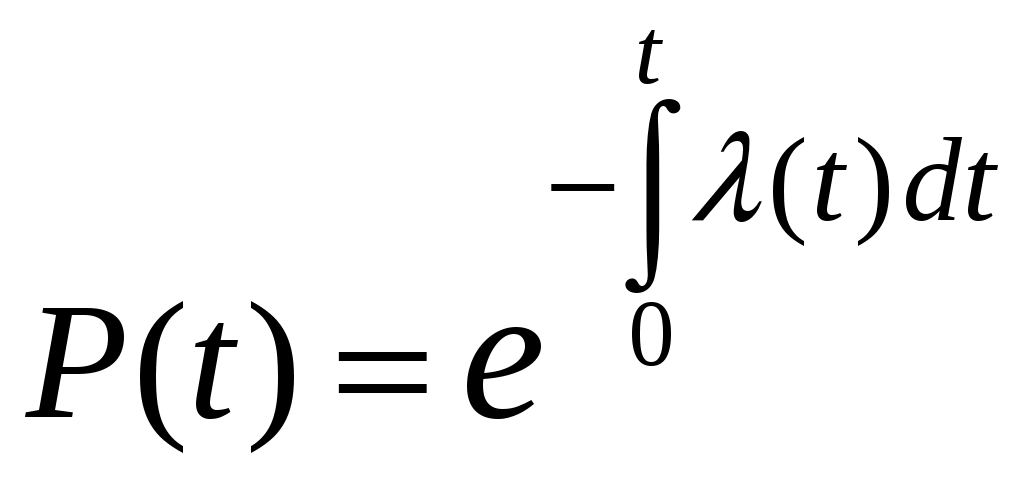(1.10)
Средней наработкой до первого отказа называется математическое ожидание времени работы элемента (системы) до первого отказа.

Математическое ожидание для вычисляется через частоту отказов по следующему выражению
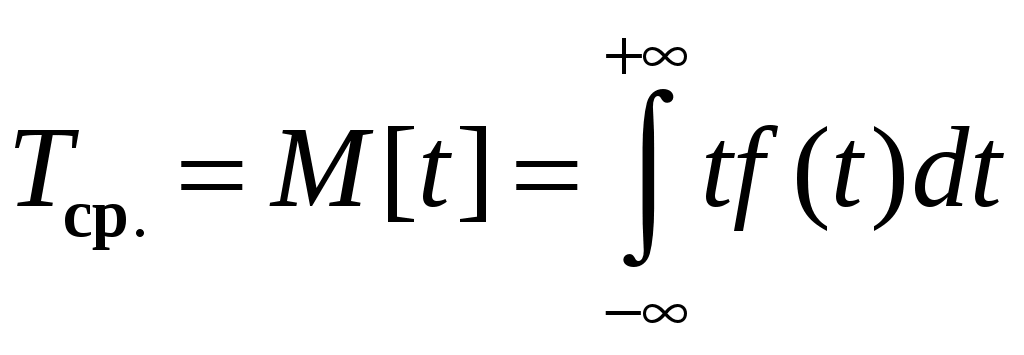. (1.11)

А так как положительно и , и , то

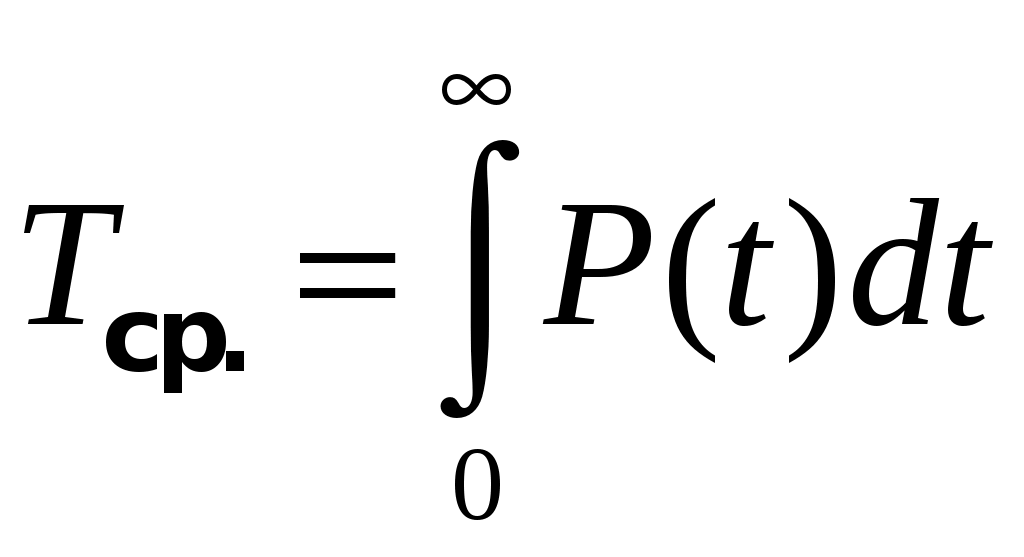(1.12)

Статистическая оценка средней наработки до первого отказа по результатам испытаний, если отказали все испытываемые элементы, вычисляется по формуле

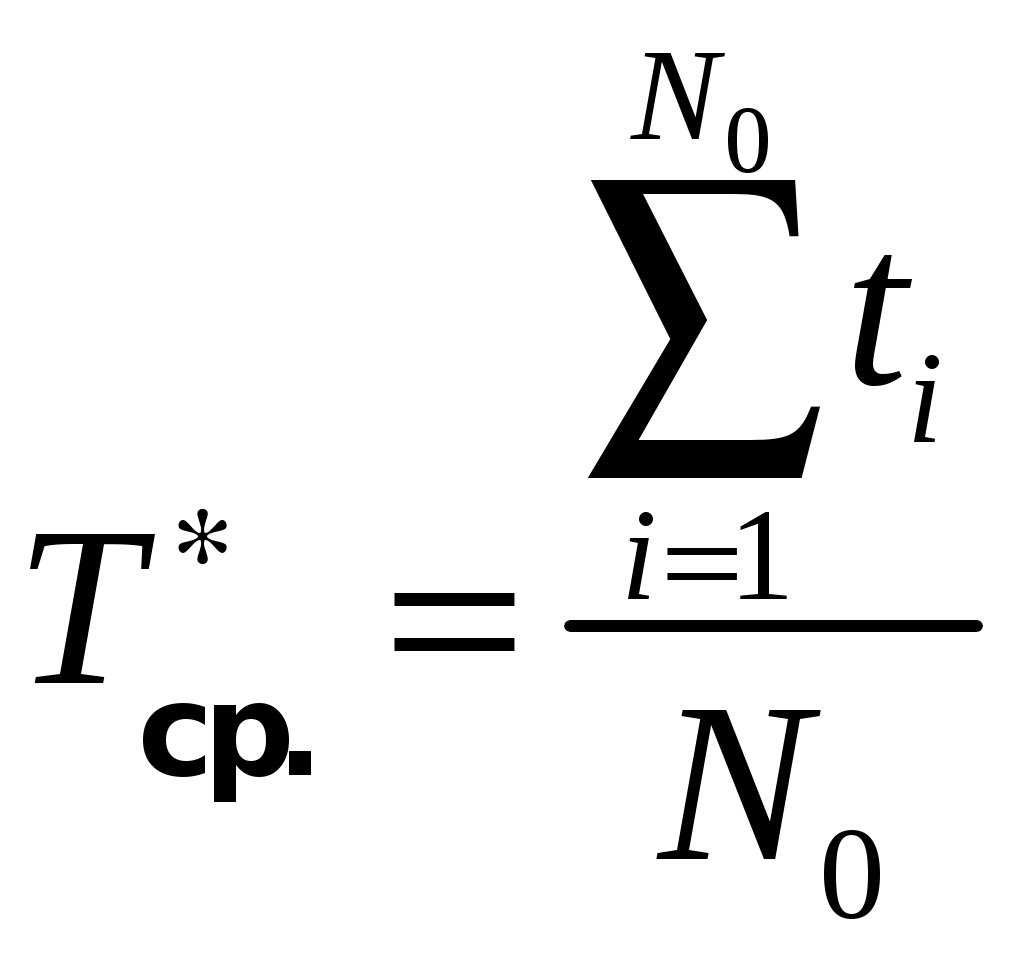, (1.13)

где – время безотказной работы i- го элемента;

– число элементов поставленных на испытания.

В том случае, если испытания производятся не до отказа всех элементов, а все время испытаний разбивается на k – интервалов, что позволяет сократить расходы на процесс испытаний, то среднюю наработку до первого отказа лучше определять по выражению

---

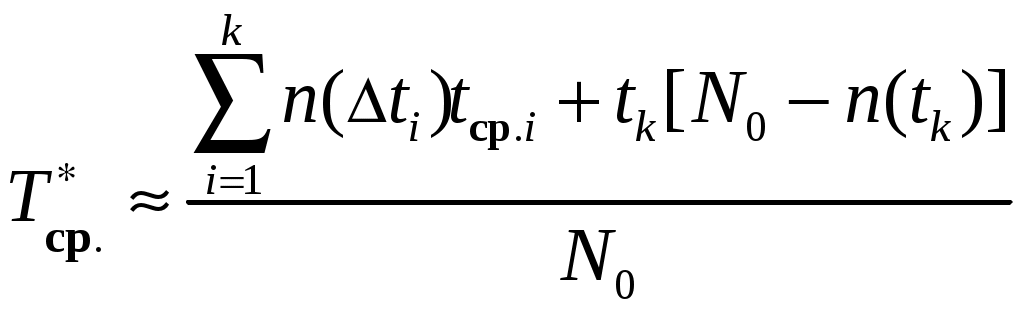
, (1.14)

где - среднее время работы элементов в i- ом интервале;

- время начала i- го интервала;

- время конца i- го интервала;

- число элементов вышедших из строя за время .
1.2 Индивидуальные задания по теме «Определение критериев

надежности невосстанавливаемых систем»

Задача 1.2.1. На испытание поставлено N₀ = 1600 образцов неремонтируемой аппаратуры. Число отказов n (t) фиксировалось через каждые 100 часов работы (t = 100 ч). Данные об отказах приведены в таблице 1.1. При этом к величине n (t) необходимо прибавить j – номер варианта (задаётся преподавателем).

Требуется определить следующие критерии надёжности: вероятность безотказной работы P^*( t ); вероятность отказа q^*( t ); интенсивность отказов ^*( t ); частоту отказов f ^*( t ); среднее время работы до первого отказа T ^*_ср .

Построить зависимости P^*( t ), q^*( t ), ^*( t ), f ^*( t ) от времени.

---

Таблица 1.1

Номер группы
1		2		3		4
 t i , ч	n (  t i)	 t i , ч	n (  t i )	 t i , ч	n (  t i )	 t i , ч	n ( t i )
0-100	44	0-100	48	0-100	51	0-100	50
100-200	42	100-200	44	100-200	46	100-200	43
200-300	37	200-300	40	200-300	42	200-300	36
300-400	31	300-400	37	300-400	36	300-400	33
400-500	28	400-500	33	400-500	32	400-500	30
500-600	25	500-600	28	500-600	29	500-600	28
600-700	20	600-700	25	600-700	25	600-700	25
700-800	17	700-800	22	700-800	20	700-800	20
800-900	16	800-900	21	800-900	17	800-900	17
900-1000	16	900-1000	22	900-1000	16	900-1000	16
1000-1100	15	1000-1100	20	1000-1100	16	1000-1100	16
1100-1200	14	1100-1200	19	1100-1200	15	1100-1200	15
1200-1300	15	1200-1300	19	1200-1300	16	1200-1300	14
1300-1400	13	1300-1400	18	1300-1400	15	1300-1400	15
1400-1500	13	1400-1500	18	1400-1500	15	1400-1500	14
1500-1600	13	1500-1600	18	1500-1600	14	1500-1600	13
1600-1700	12	1600-1700	19	1600-1700	13	1600-1700	12
1700-1800	13	1700-1800	18	1700-1800	14	1700-1800	13
1800-1900	14	1800-1900	20	1800-1900	15	1800-1900	14
1900-2000	15	1900-2000	24	1900-2000	16	1900-2000	15

---

Задача 1.2.2 Время работы до отказа подчинено усечённому нормальному закону с параметрами T₁ = 12000 + 180*k*( -1 ) ^k – ( -1 ) ^j 70j

( где k — номер группы; j — номер варианта ),  = 1200 + 160k + ( -1 ) ^j 25j.

Требуется вычислить и построить графики p( t ), f( t ), ( t ), а также определить среднее время работы до первого отказа Т _ср .
Задача 1.2.3 В результате анализа данных об отказах изделий установлено, что один из критериев надёжности определяется выражением, которое выбирается в соответствии с номером группы и вариантом, представленных соответственно в таблицах 1.2 и 1.3.
Требуется найти остальные количественные характеристики надёжности — p( t ), f( t ), ( t ), f _ср( t ), Т _ср.

Построить графики p( t ), f( t ), ( t ), f _ср( t ).
1.3 Определение критериев восстанавливаемых систем

Основной количественной характеристикой надёжности восстанав-ливаемых изделий (систем), если не учитывать время восстановления, является параметр потока отказов f_cp(t) (средняя частота отказов).

Параметром потока отказов называется отношение числа отказавших изделий в единицу времени к числу испытываемых изделий при условии, что все вышедшие из строя изделия заменяются исправными.

Статистическая оценка параметра потока отказов определяется выражением

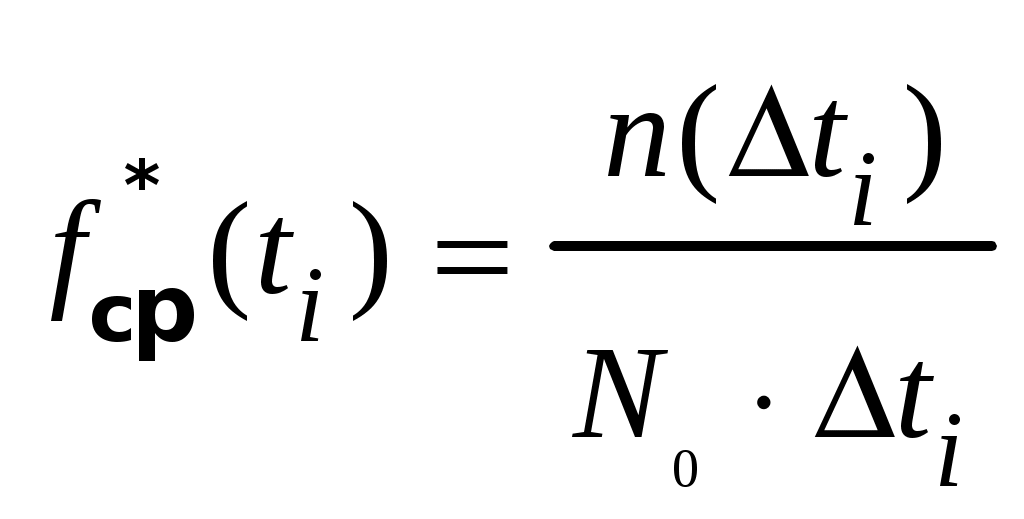, (1.16)

где - число испытываемых образцов;

- число отказавших образцов в интервале времени от t –Δt/2доt + Δt/2;

- интервал времени, для которого определяется параметр потока отказов.

---