Файл: В. Н. Коваленко надежность устройств железнодорожной автоматики, телемеханики и связи.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.12.2023
Просмотров: 367
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таблица 1.2
| Номер группы | Интенсивность отказов | |||
| , 10 –6 1/час | k, 10 –6 1/час | 1, 10 –6 1/час | 2, 10 –6 1/час | |
| 1 | 0,25 | 1,3 | 1,4 | 0,8 |
| 2 | 0,8 | 0,7 | 0,85 | 0,25 |
| 3 | 1,0 | 0,7 | 1,3 | 1,3 |
| 4 | 3,5 | 3,2 | 0,6 | 1,35 |
Таблица 1.3
| № вар. | Результат анализа данных об отказах | № вар. | Результат анализа данных об отказах |
| 1 | | 14 | |
| 2 | | 15 | |
| 3 | | 16 | |
| 4 | | 17 | |
| 5 | | 18 | |
| 6 | | 19 | |
| 7 | ( t ) = k2 t /( 1 + kt ) | 20 | |
| 8 | f( t ) = k2 t e – k t | 21 | |
| 9 | | 22 | |
| 10 | | 23 | |
| 11 | | 24 | |
| 12 | 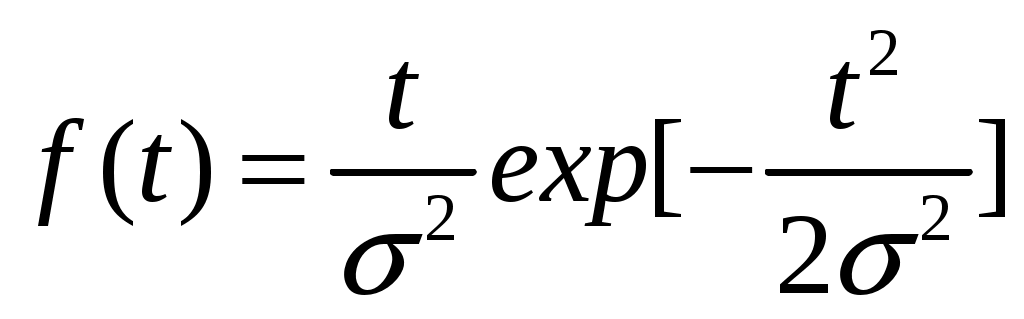 | 25 | |
| 13 | | 26 | |
Параметр потока отказов и частота отказов для ординарных
потоков с ограниченным последствием и при мгновенном восстановлении связаны между собой интегральным уравнением Вольтера второго рода
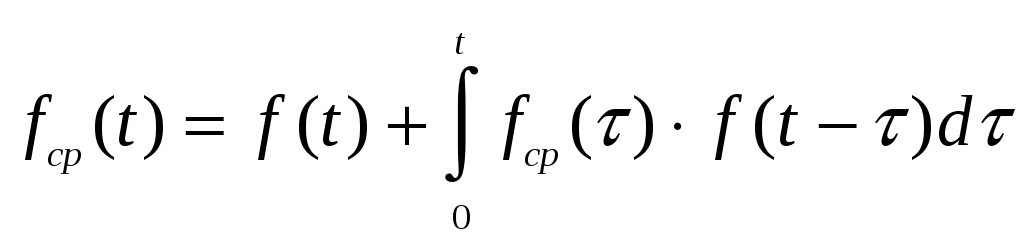 (1.17)
(1.17)Как правило, уравнение (1.17) решается в операторной форме
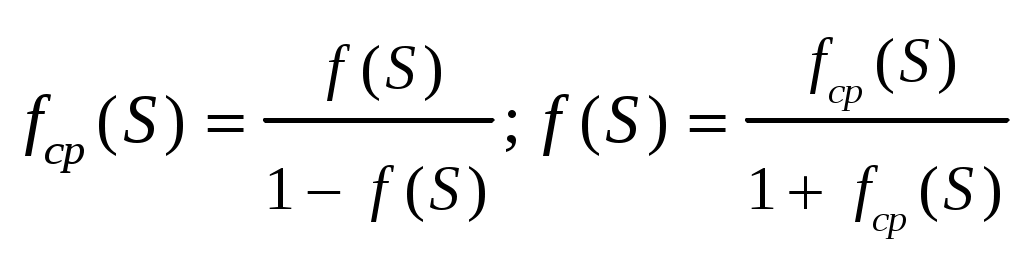 (1.18)
(1.18)где
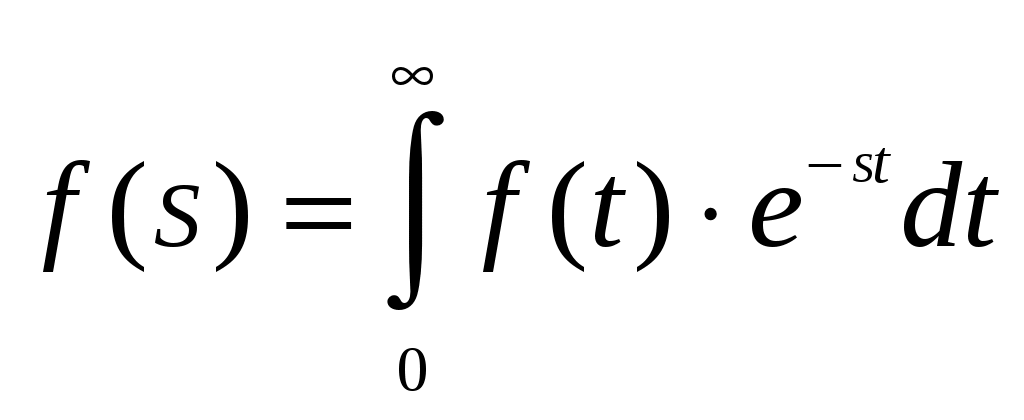 - изображение частоты отказов по Лапласу.
- изображение частоты отказов по Лапласу.Представленные соотношения (1.18) позволяют найти одну характеристику через другую, если существуют прямое преобразование
функций
Наработкой на отказ называется среднее значение времени между соседними отказами.
Оценочное значение этой характеристики определяется по статистическим данным об отказах по выражению
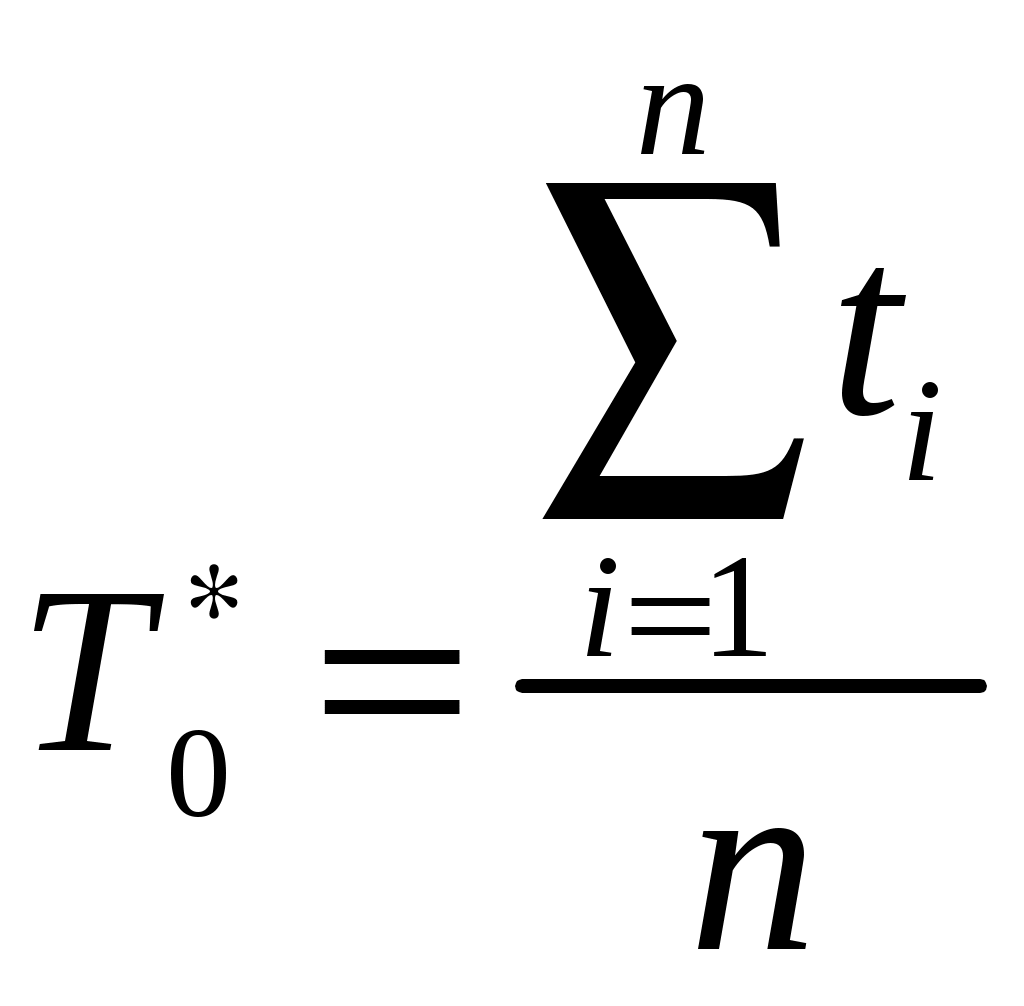 , (1.19)
, (1.19)где
В том случае, если на испытания поставлено N0образцов, то
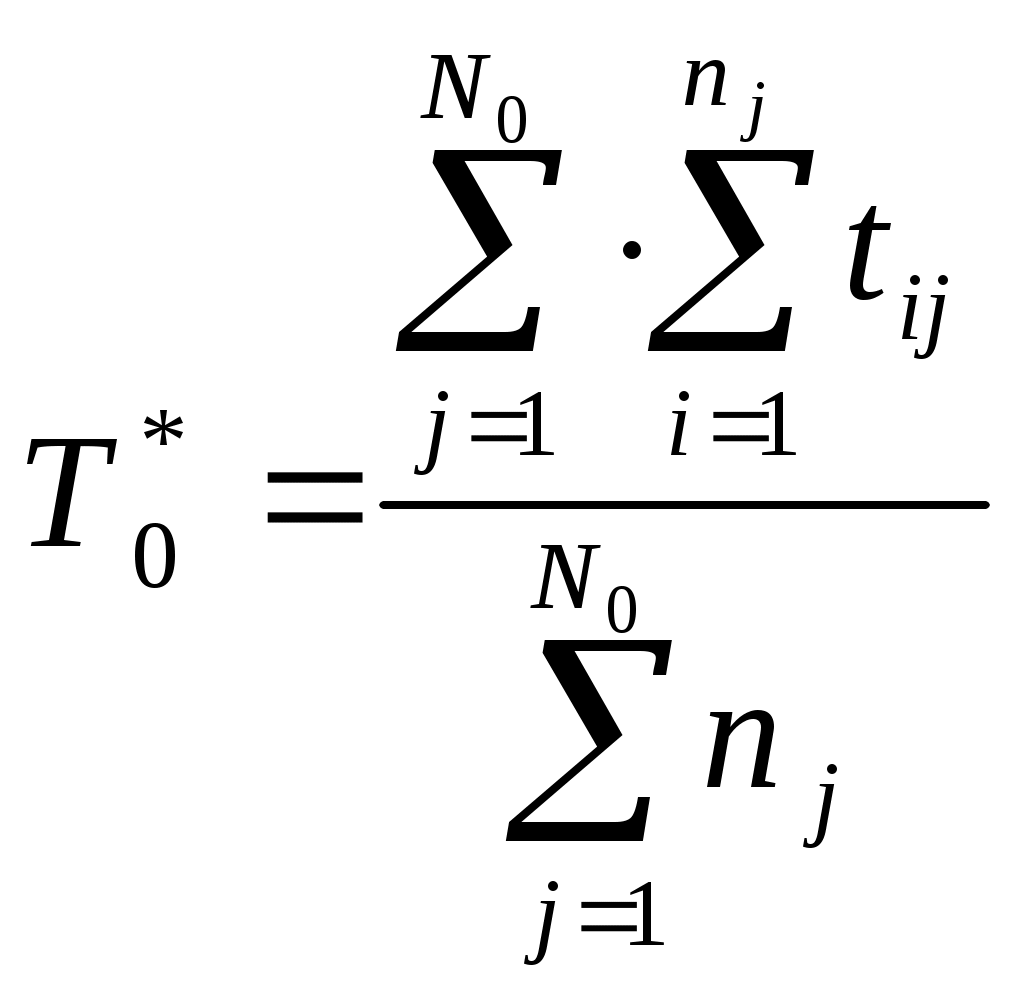 (1.20)
(1.20)где
Под коэффициентом использования понимается отношение суммарного времени исправной работы к суммарному времени исправной работы и простоев за один и тот же календарный срок. Этот коэффициент обозначается
Согласно данному определению
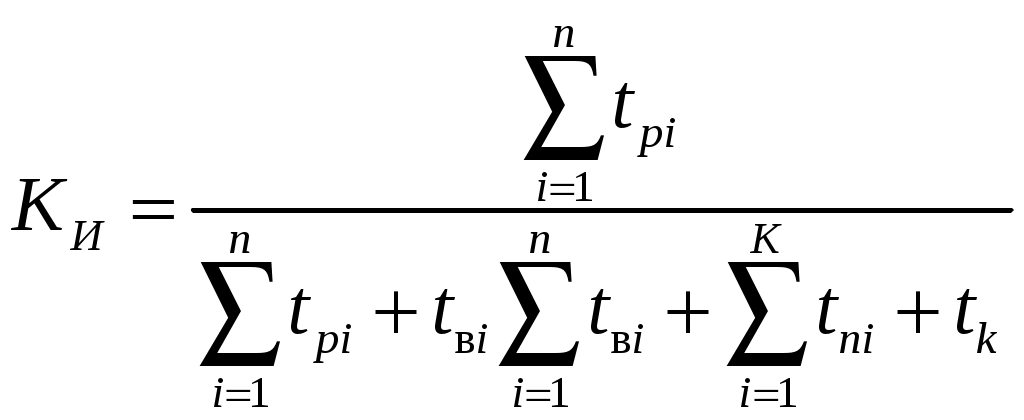 , (1,21)
, (1,21)где
причине отказов и проведения профилактик;
n – число остановок за определенный календарный срок, для которого определяется коэффициент использования;
Коэффициентом готовности называется отношение суммарного времени исправной работы к суммарному времени исправной работы и восстановлений, взятых за один и тот же календарный срок
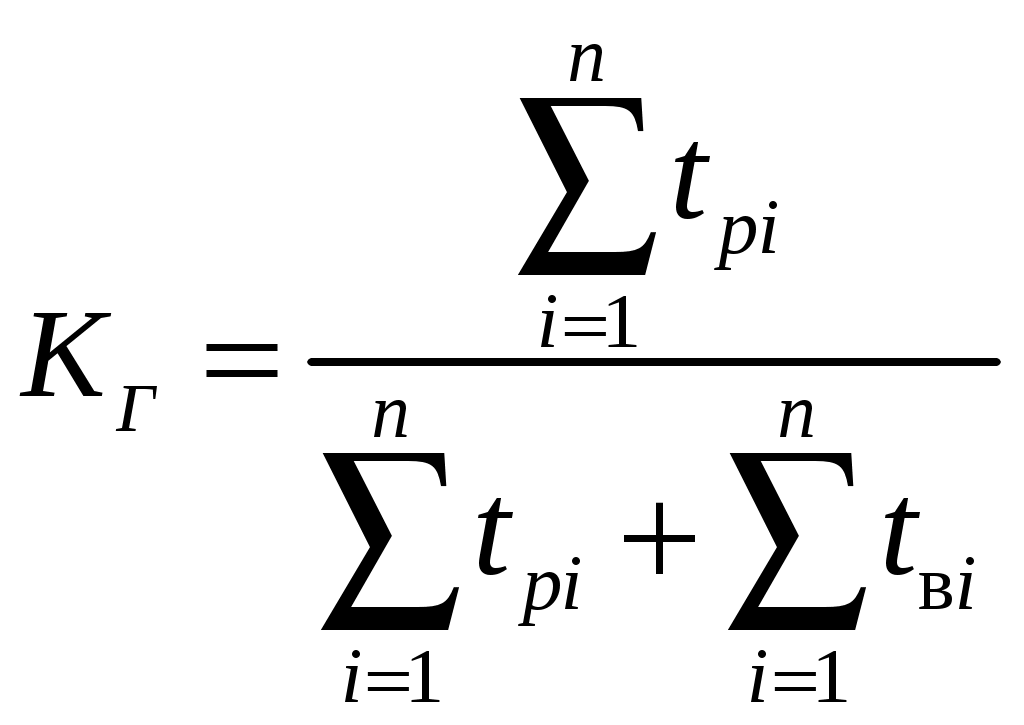 , (1.22)
, (1.22)где
n – число отказов изделия.
В том случае, если поток отказов простейший, то КГ обычно вычисляют по формуле
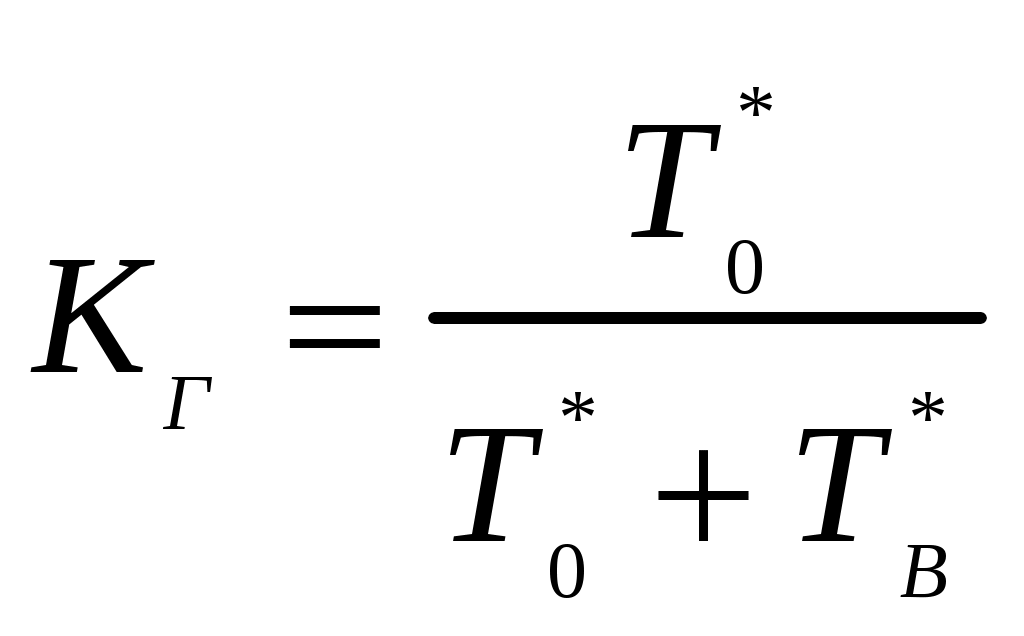 , (1.23)
, (1.23)где
Выражение (1.23) является статистическим определением коэффициента готовности. Для перехода к вероятностной трактовке величины
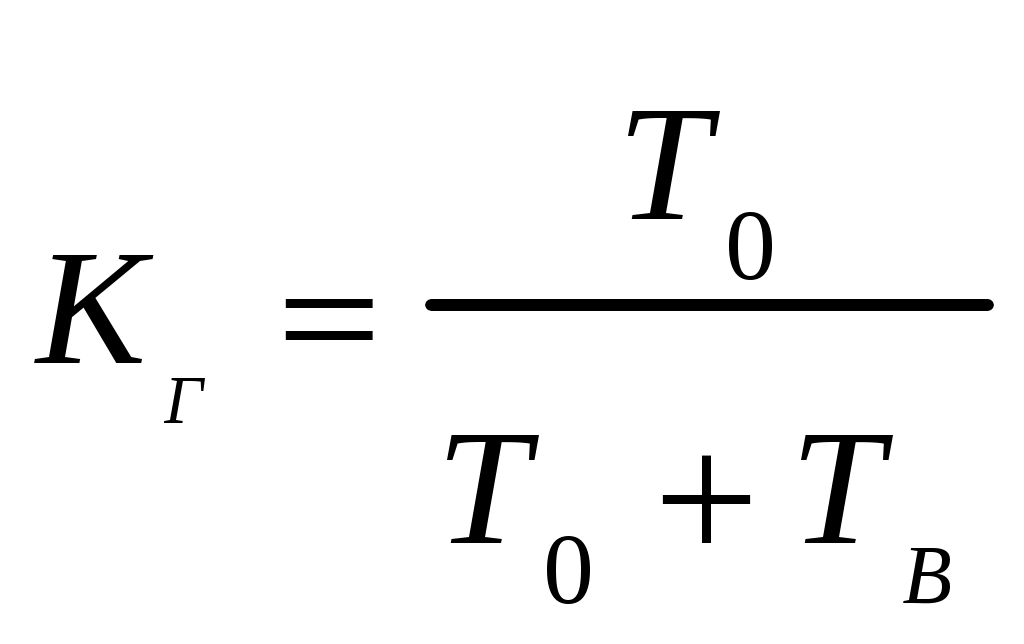 , (1.24)
, (1.24)где
Коэффициентом простоя называется отношение времени вынужденных простоев к сумме времени исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок.
Согласно определению
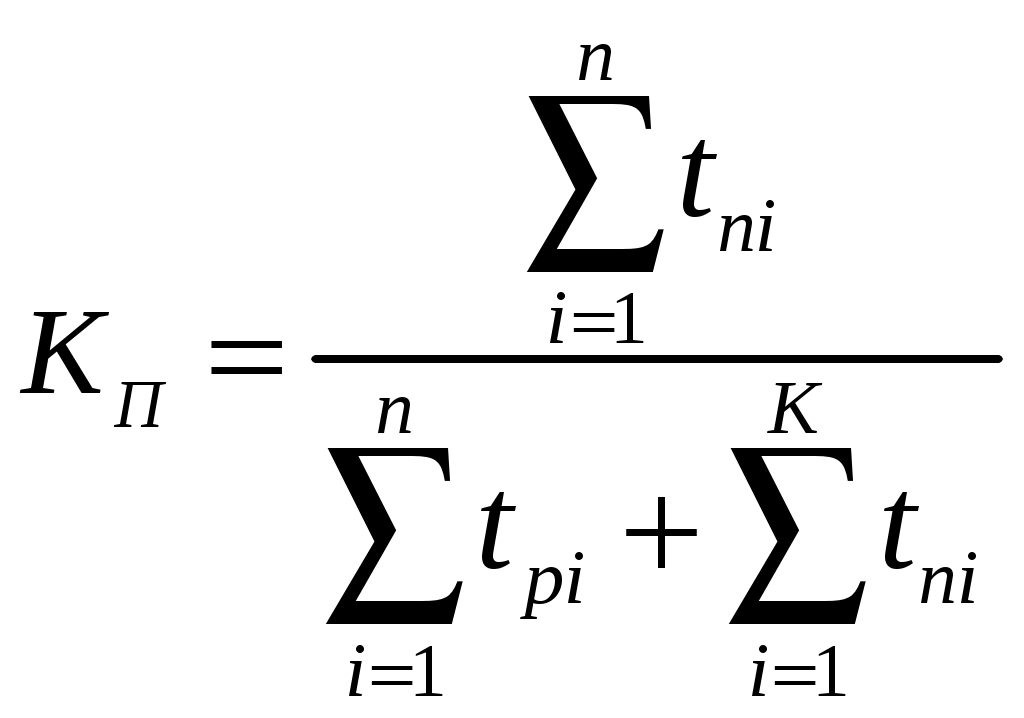 . (1.25)
. (1.25)Как следует из определений коэффициента простоя
Среднее время восстановления представляет собой математическое ожидание времени восстановления и определяется следующим выражением
Статистическая оценка среднего времени восстановления определяется выражением
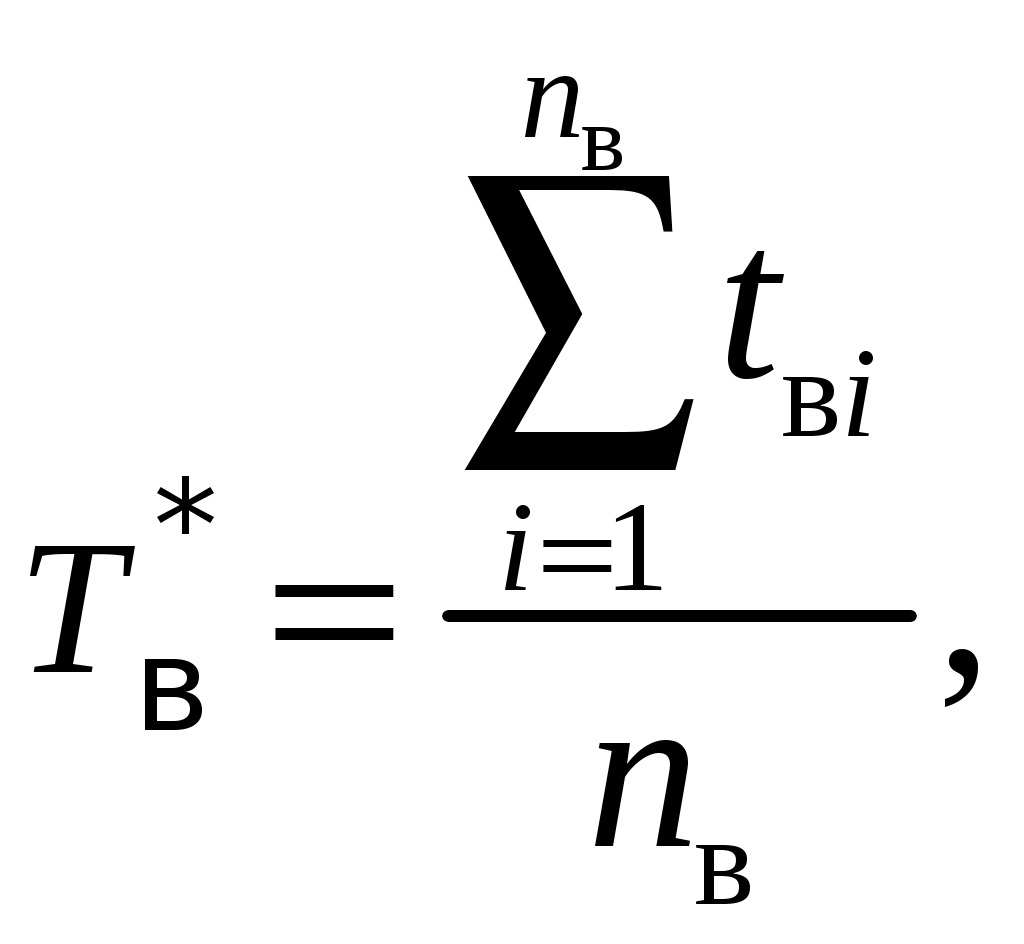 (1.28)
(1.28)где
В том случае, если известно распределение отказов отдельных элементов системы и время, затраченное на их устранение (время восстановления), то оценку среднего времени восстановления можно определить из выражения
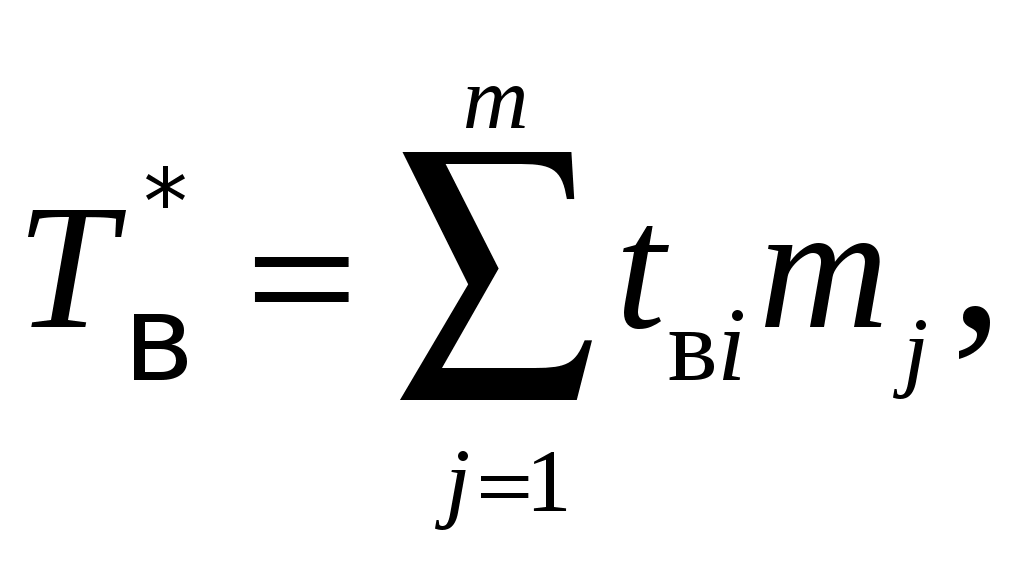 (1.29)
(1.29)где
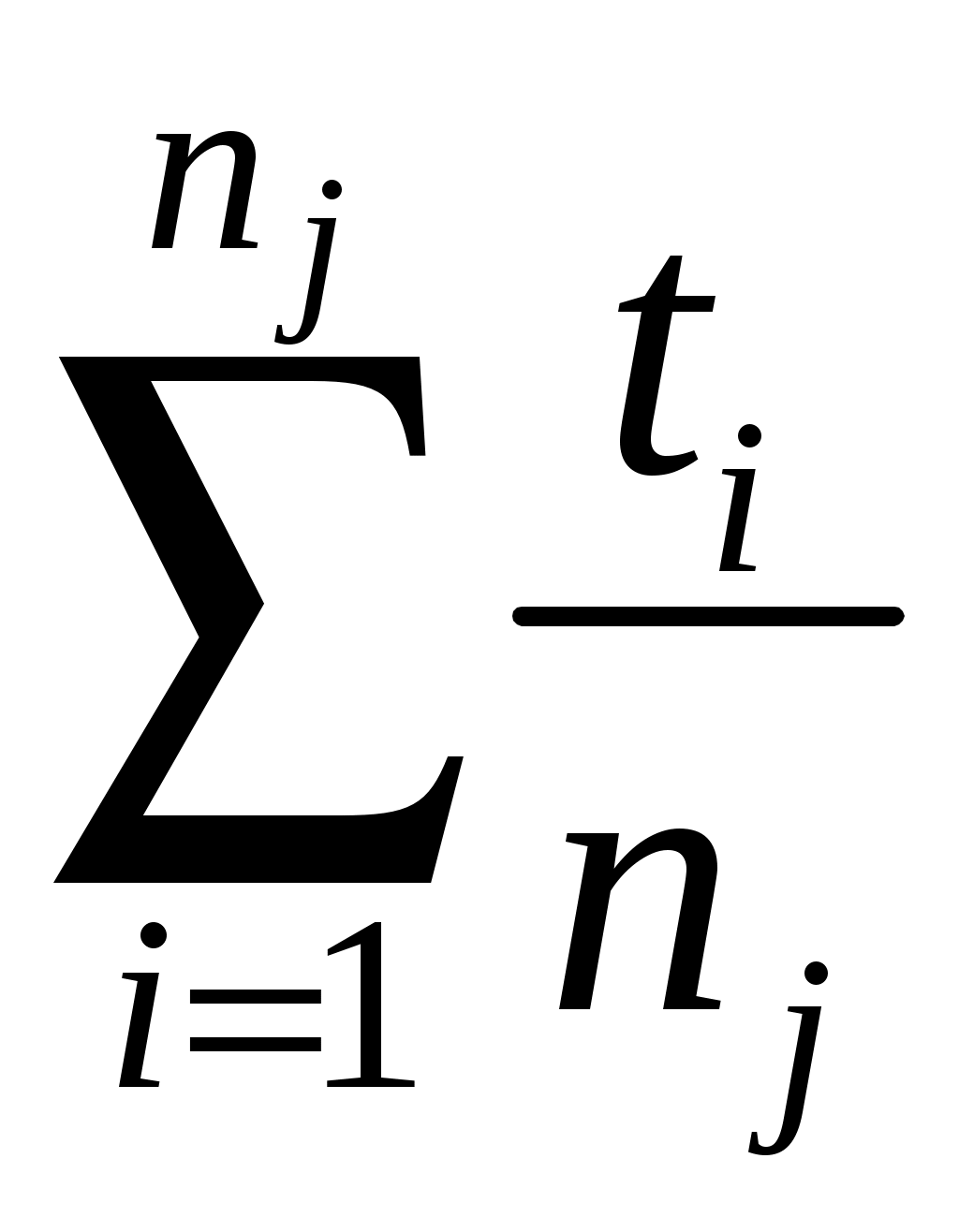 – среднее время восстановления
– среднее время восстановления Необходимо помнить, что вероятность отказа в начале эксплуатации мала, а с течением времени эксплуатации эта вероятность возрастает. Это означает то, что вероятность застать систему в исправном состоянии в начале эксплуатации будет выше, чем по истечении некоторого времени.
Выражение, которое устанавливает зависимость между коэффициентом готовности и вероятностью застать систему в исправном состоянии в любой момент времени
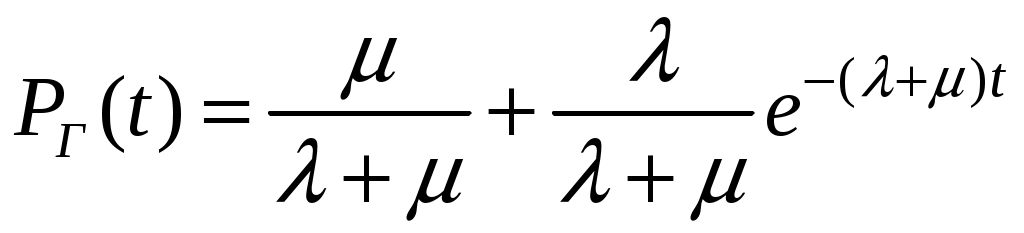
где
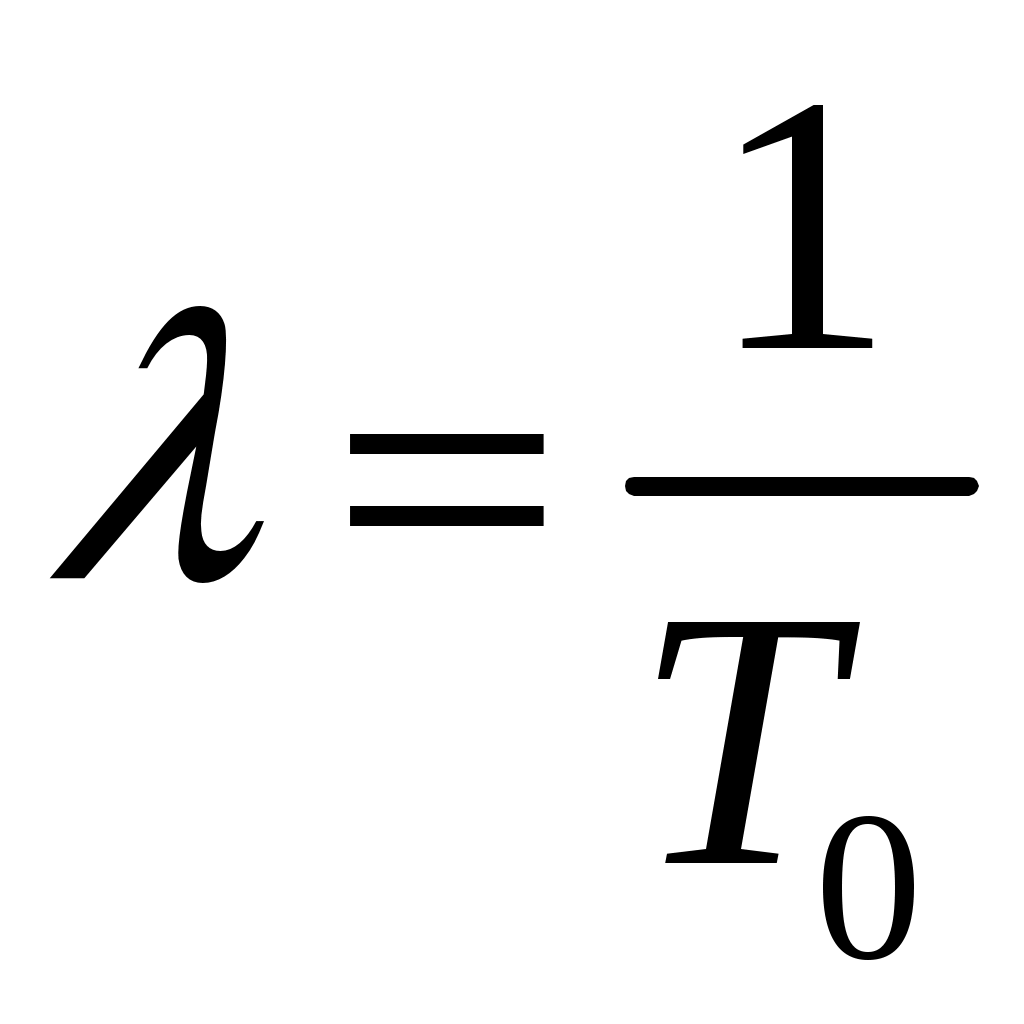 - интенсивность отказов системы;
- интенсивность отказов системы;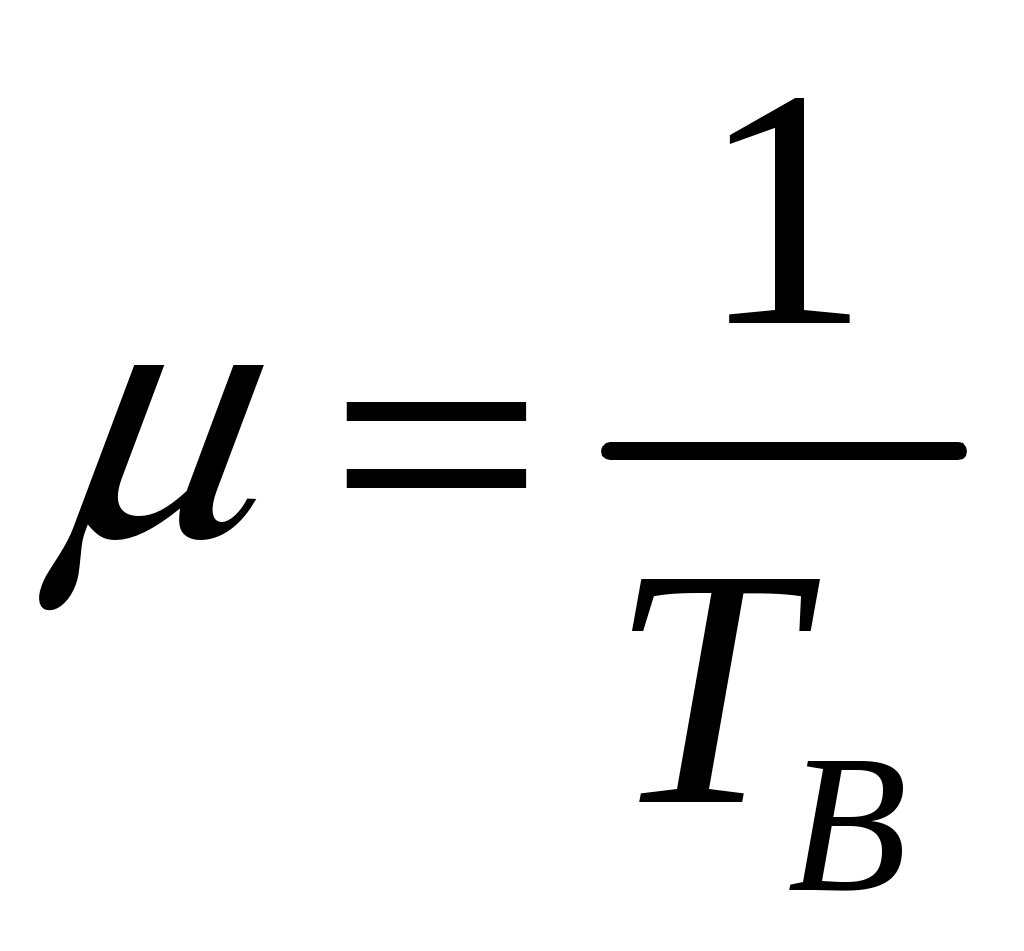 - интенсивность восстановления системы;
- интенсивность восстановления системы;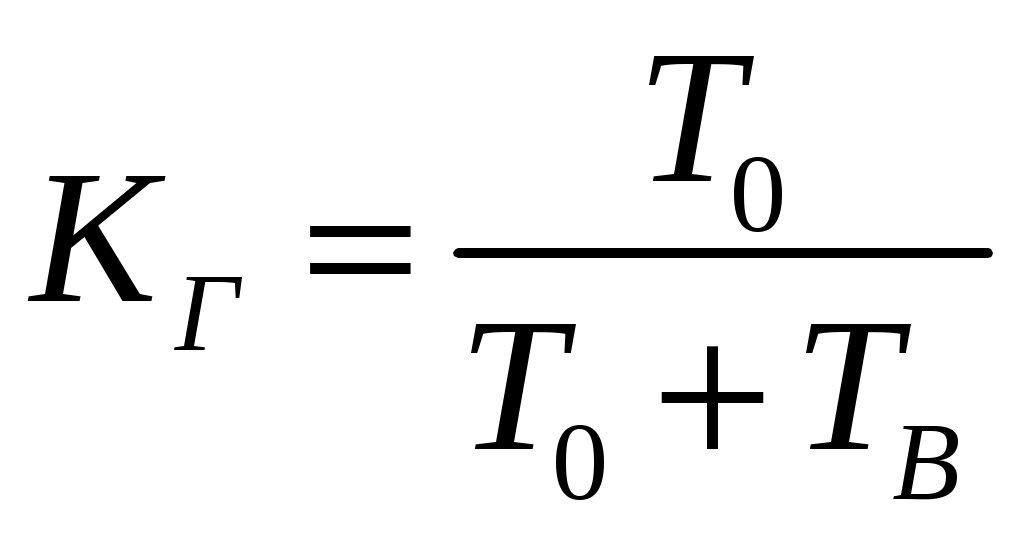 - коэффициент готовности системы
- коэффициент готовности системы1.4 Индивидуальные задания по теме «Определение
критериев восстанавливаемых систем»
Задача 1.3.1 При эксплуатации системы автоматики было зафик-сировано n = 25 + j + 2k отказов ( j – номер варианта, задаётся препо-давателем, k – номер группы ) в течение ( 600 + j + 2k ) ч. При этом распределение отказов по элементам и время затраченное на их устранение ( время восстановления ), приведены в таблице 1.4.
Время, затраченное на проследование к месту отказа и профилактику, в среднем больше времени восстановления в 1,6 раза.
Требуется определить:
-
среднее время восстановления t*вс ; -
среднюю наработку на отказ – Т0; -
коэффициент готовности ( k г ), использования (k и ), простоя (k п ).
Задача 1.3.2 В результате эксплуатации N = 1600 восстанавливаемых изделий получены следующие статистические данные об отказах, представленные в таблице 1.5. Число отказовn(t i) фиксировалось через t i часов. При этом к числу отказовn(t i) прибавляется номер варианта j (номер варианта задается преподавателем).
Необходимо определить:
-
среднюю наработку до первого отказа изделия Т ср ; -
вероятность безотказной работы Р( t ); -
среднюю частоту отказов (параметр потока отказов) f ср( t) ; -
частоту отказов f( t ); -
интенсивность отказов ( t ).
Пример решение задачи данного типа смотри в /2,4/.
Таблица 1.4
| Элементы системы | Количество отказов n i | Время восстановления t в, мин | Суммарное время восстановления ti , мин |
| Полупроводниковые элементы | 6 | 35 + j + k 19 + j + k 21 + j + k 30 + j + k 19 + j + k 16 + j + k | — |
| Реле | 3 | 12 + j + k 19 + j +k 18 + j + k | — |
| Резисторы | 5 + 2k | — | 90 + j + 5k |
| Конденсаторы | 7 + 2k | — | 125 + j + 9k |
| Провода | 3 + 2k | — | 99 |
| Пайки | j | — | 100 + 2j + 6k |
Таблица 1.5
| Номер группы | |||||||
| 1 | 2 | 3 | 4 | ||||
| t i , ч | N ( t i) | t i , ч | n ( t i ) | t i , ч | n ( t i ) | t i , ч | n ( t i ) |
| 0-200 | 48 | 0-200 | 50 | 0-200 | 56 | 0-200 | 48 |
| 200-400 | 42 | 200-400 | 44 | 200-400 | 50 | 200-400 | 40 |
| 400-600 | 38 | 400-600 | 40 | 400-600 | 45 | 400-600 | 35 |
| 600-800 | 34 | 600-800 | 36 | 600-800 | 41 | 600-800 | 33 |
| 800-1000 | 32 | 800-1000 | 33 | 800-1000 | 37 | 800-1000 | 30 |
| 1000-1200 | 30 | 1000-1200 | 30 | 1000-1200 | 34 | 1000-1200 | 28 |
| 1200-1400 | 28 | 1200-1400 | 28 | 1200-1400 | 31 | 1200-1400 | 25 |
| 1400-1600 | 26 | 1400-1600 | 26 | 1400-1600 | 29 | 1400-1600 | 20 |
| 1600-1800 | 26 | 1600-1800 | 26 | 1600-1800 | 27 | 1600-1800 | 17 |
| 1800-2000 | 25 | 1800-2000 | 25 | 1800-2000 | 25 | 1800-2000 | 16 |
| 2000-2200 | 25 | 2000-2200 | 25 | 2000-2200 | 25 | 2000-2200 | 16 |
| 2200-2400 | 25 | 2200-2400 | 24 | 2200-2400 | 24 | 2200-2400 | 15 |
| 2400-2600 | 24 | 2400-2600 | 24 | 2400-2600 | 24 | 2400-2600 | 14 |
| 2600-2800 | 24 | 2600-2800 | 24 | 2600-2800 | 24 | 2600-2800 | 15 |
| 2800-3000 | 24 | 2800-3000 | 24 | 2800-3000 | 23 | 2800-3000 | 14 |
| 3000-3200 | 23 | 3000-3200 | 23 | 3000-3200 | 23 | 3000-3200 | 13 |
| 3200-3400 | 23 | 3200-3400 | 23 | 3200-3400 | 23 | 3200-3400 | 12 |
| 3400-3600 | 23 | 3400-3600 | 23 | 3400-3600 | 23 | 3400-3600 | 13 |
| 3600-3800 | 23 | 3600-3800 | 22 | 3600-3800 | 22 | 3600-3800 | 12 |
| 3800-4000 | 23 | 3800-4000 | 22 | 3800-4000 | 22 | 3800-4000 | 14 |
2. РАСЧЕТ НАДЕЖНОСТИ НЕВОССТАНАВЛИВАЕМЫХ
СИСТЕМ ПРИ ОСНОВНОМ СОЕДИНЕНИИ ЭЛЕМЕНТОВ
2.1 Цели, задачи и этапы расчета надежности систем
В современных системах железнодорожной автоматики и телемеханики отказ даже одного элемента может привести к исключительно серьезным последствиям /8/. Исходя из этого основной задачей при проектировании системы является выбор наилучших конструктивных, механических, электрических и других параметров системы с учетом стоимости и надежности. Поэтому для достижения этой цели необходимо проводить оценку надежности системы на этапе проектирования. При этом используются априорные показатели надежности элементов с учетом действия возможных нагрузок и внешних факторов, которые лишь приближенно характеризуют процессы при эксплуатации технической системы. В месте с тем такой анализ позволяет еще на стадии проектирования выявить слабые с точки зрения надежности и безопасности места в конструкции, принять необходимые меры к их устранению, а также отклонить неудовлетворительные варианты построения системы. Предварительная оценка надежности системы и ее компонентов служит основой разработки правил ее эксплуатации, назначения регламентов и сроков контроля, испытаний и планово-предупредительных ремонтов, а также завершения жизненного цикла. Следовательно, априорный расчет надежности имеет важное значение, в практике проектирования систем железнодорожной автоматики и телемеханики и составляет неотъемлемую часть технических проектов.
Основные условия обеспечения надежности состоят в строгом выполнении правила, называемого триадой надежности: надежность закладывается при проектировании, обеспечивается при изготовлении и поддерживается в эксплуатации /1/. Без строгого выполнения этого правила нельзя решить задачу создания высоконадежных систем путем компенсации недоработок предыдущего этапа на последующем.
Каждому этапу разработки или модернизации системы соответствует определенный уровень расчета надежности. Как правило, выделяют три уровня расчетов: прикидочный, ориентировочный и окончательный.
На стадии прикидочного и ориентировочного расчетов предполагается, что объект собран по основной схеме (т.е элементы в объекте соединены последовательно относительно надежности), интенсивность отказов всех элементов не зависит от времени, т. е.
любой отказ не вызывает изменения характеристик (работоспособности) элементов, кроме отказавшего, т. е. поток отказов принимается простейшим.
В реальных условиях эксплуатации элементы, из которых собрана система, в большинстве случаев оказываются в условиях, значительно отличающихся от расчетных (номинальных). Это обстоятельство влияет как на надежность элементов, так и на систему в целом.
Для систем железнодорожной автоматики и телемеханики наиболее существенными факторами являются: электрическая нагрузка и скорость ее изменения; температура, механические воздействия (вибрация, тряски, удары); влажность окружающего воздуха; наличие пыли в воздухе и др.
Как правило, эти факторы учитываются с помощью соответствующих поправочных коэффициентов. При этом интенсивность отказов элемента определяется по выражению
где