Файл: В. Н. Коваленко надежность устройств железнодорожной автоматики, телемеханики и связи.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.12.2023
Просмотров: 366
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3
4
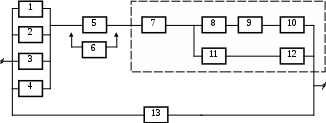
Рисунок 3.1, лист 2
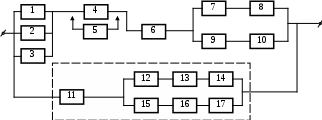
5
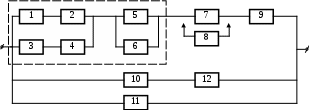
6
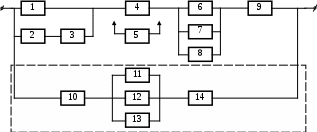
7
Рисунок 3.1, лист 3
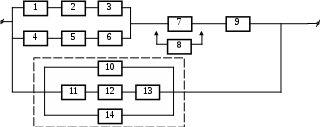
8
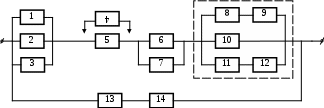
9
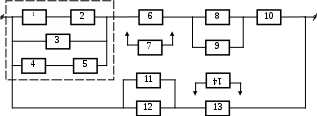
10
Рисунок 3.1, лист 4
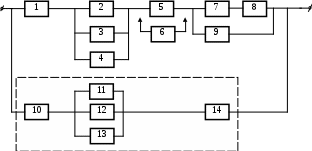
11
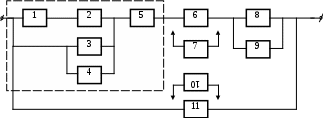
12
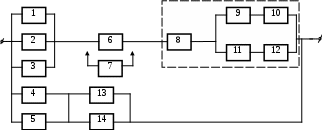
13
Рисунок 3.1, лист 5
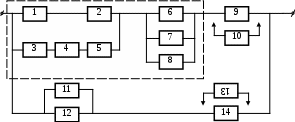
14
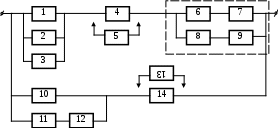
15
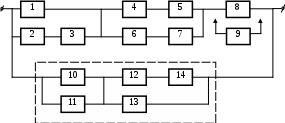
16
Рисунок 3.1, лист 6
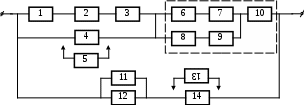
17
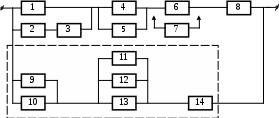
18
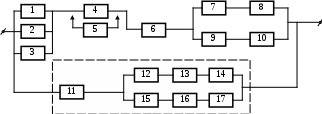
19
Рисунок 3.1, лист 7
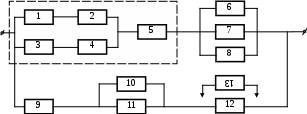
20
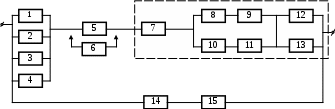
21
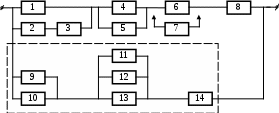
22
Рисунок 3.1, лист 8

23

24
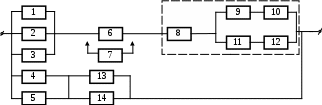
25
Рисунок 3.1, лист 9
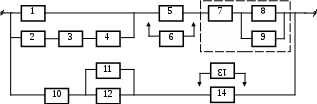
26
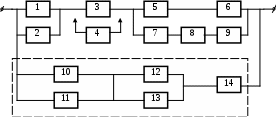
27
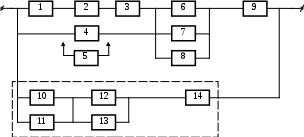
28
Рисунок 3.1, лист 10
Задача 3.3.2. Система содержит n групп элементов
, каждая j - группа, в свою очередь, содержит Nj элементов, причём j – интенсивность отказов
элементов j– группы. Вероятность безотказной работы системы за время t равна РK(t). Требуется определить число элементов ЗИПа. Исходные данные для расчёта приведены в таблице 3.2.
Таблица 3.2
| № вар. | PK(t) | t,ч | n | Реле | Резисторы | Конденсатор | Диоды | Транзисторы | |||||
| N1 | 1*10-5 | N2 | 2*10-5 | N3 | 3*10-6 | N4 | 4*10-6 | N5 | 5*10-6 | ||||
| 1 | 0,98 | 10000 | 4 | 50 | 2 | 80 | 0,5 | 50 | 1,2 | 15 | 0,7 | — | — |
| 2 | 0,96 | 12000 | 4 | — | — | 10 | 0,6 | 80 | 1,8 | 14 | 5 | 46 | 4 |
| 3 | 0,94 | 8000 | 5 | 20 | 5 | 80 | 1,0 | 60 | 2,0 | 28 | 2 | 38 | 3 |
| 4 | 0,88 | 10000 | 3 | 80 | 1,1 | 50 | 1,6 | 60 | 1,2 | — | — | — | — |
| 5 | 0,9 | 11000 | 5 | 40 | 0,3 | 60 | 0,5 | 47 | 2,0 | 26 | 1,5 | 48 | 4,6 |
| 6 | 0,89 | 15000 | 4 | 30 | 0,4 | 80 | 0,45 | 60 | 1,6 | 25 | 0,5 | 37 | 2,6 |
| 7 | 0,84 | 20000 | 5 | 20 | 1,2 | 42 | 0,4 | 48 | 1,4 | 36 | 2 | 40 | 5 |
| 8 | 0,9 | 16000 | 4 | 60 | 1,4 | 30 | 0,5 | 57 | 1,4 | 25 | 0,7 | — | — |
| 9 | 0,84 | 20000 | 5 | 10 | 0,5 | 50 | 0,6 | 48 | 2 | 34 | 0,5 | 43 | 1 |
| 10 | 0,82 | 12000 | 4 | 80 | 0,6 | 40 | 0,8 | 35 | 1,2 | 28 | 5 | — | — |
| 11 | 0,88 | 10000 | 5 | 12 | 0,7 | 20 | 1,2 | 45 | 1,6 | 34 | 2,5 | 37 | 1,7 |
| 12 | 0,9 | 5000 | 4 | — | — | 32 | 1,2 | 60 | 1,2 | 36 | 2 | 54 | 4 |
| 13 | 0,84 | 6000 | 4 | 80 | 0,8 | 40 | 1,6 | 36 | 1,6 | — | — | 42 | 1,7 |
| 14 | 0,88 | 10000 | 5 | 20 | 1,2 | 35 | 0,2 | 40 | 1,8 | 28 | 0,7 | 32 | 3 |
| 15 | 0,86 | 15000 | 4 | 10 | 1,4 | 42 | 0,4 | 54 | 1,2 | 45 | 2 | 40 | 2,6 |
| 16 | 0,88 | 12000 | 5 | 18 | 1,5 | 26 | 0,5 | 50 | 1,4 | 28 | 0,7 | 37 | 2,6 |
| 17 | 0,82 | 11000 | 5 | 20 | 1,7 | 38 | 0,6 | 46 | 1,6 | 33 | 2,5 | 29 | 3 |
| 18 | 0,8 | 14000 | 5 | 50 | 1,2 | 44 | 1,2 | 72 | 1,2 | 38 | 5 | 41 | 1 |
| 19 | 0,82 | 14000 | 5 | 18 | 0,8 | 30 | 1,2 | 34 | 18 | 45 | 0,7 | 32 | 1 |
| 20 | 0,88 | 20000 | 5 | 17 | 0,7 | 20 | 0,5 | 35 | 1,6 | 28 | 2,5 | 30 | 1 |
| 21 | 0,85 | 15000 | 4 | 15 | 1,2 | 38 | 0,15 | 48 | 1,4 | - | - | 45 | 1,2 |
| 22 | 0,92 | 17000 | 5 | 20 | 1,4 | 36 | 0,2 | 36 | 1,6 | 28 | 2,5 | 40 | 0,95 |
| 23 | 0,89 | 14000 | 5 | 18 | 1,6 | 39 | 0,26 | 18 | 0,75 | 35 | 0,6 | 18 | 1,1 |
| 24 | 0,87 | 18000 | 2 | - | - | 44 | 1,1 | 25 | 0,8 | 30 | 0,9 | 25 | 0,85 |
| 25 | 0,95 | 16000 | 5 | 10 | 0,8 | 35 | 0,5 | 30 | 0,75 | 20 | 1,1 | 35 | 1,3 |
4 ОЦЕНКА И КОНТРОЛЬ НАДЕЖНОСТИ УСТРОЙСТВ ПО
РЕЗУЛЬТАТАМ ИХ ИСПЫТАНИЙ
4.1 Оценка надежности устройств
В том случае, если закон распределения времени безотказной работы элементов и систем известен, то в результате эксплуатации или испытаний могут быть найдены оценки параметров закона распределения и все необходимые характеристики их надежности. По данным полученным в результате эксплуатации или испытаний могут быть получены как точечные, так и интервальные оценки необходимого параметра надежности. В случае интервальной оценки определяется, какой интервал оценок с заданной доверительной вероятностью
Доверительный интервал определяется соотношением (4.1) и характеризует степень достоверности результатов двусторонней оценки
где
Однако в практических целях иногда достаточно определить лишь одну из границ интервала, нижнюю или верхнюю, которые соответственно определяются вероятностями
Вероятности
В случае экспоненциального распределения, которое характерно для внезапных отказов элементов и систем, плотность вероятности его распределения определяется уравнением
где
Принимая во внимания, что при экспоненциальном законе распределения
выражения для определения нижней и верхней границы значения вероятности безотказной работы и параметра
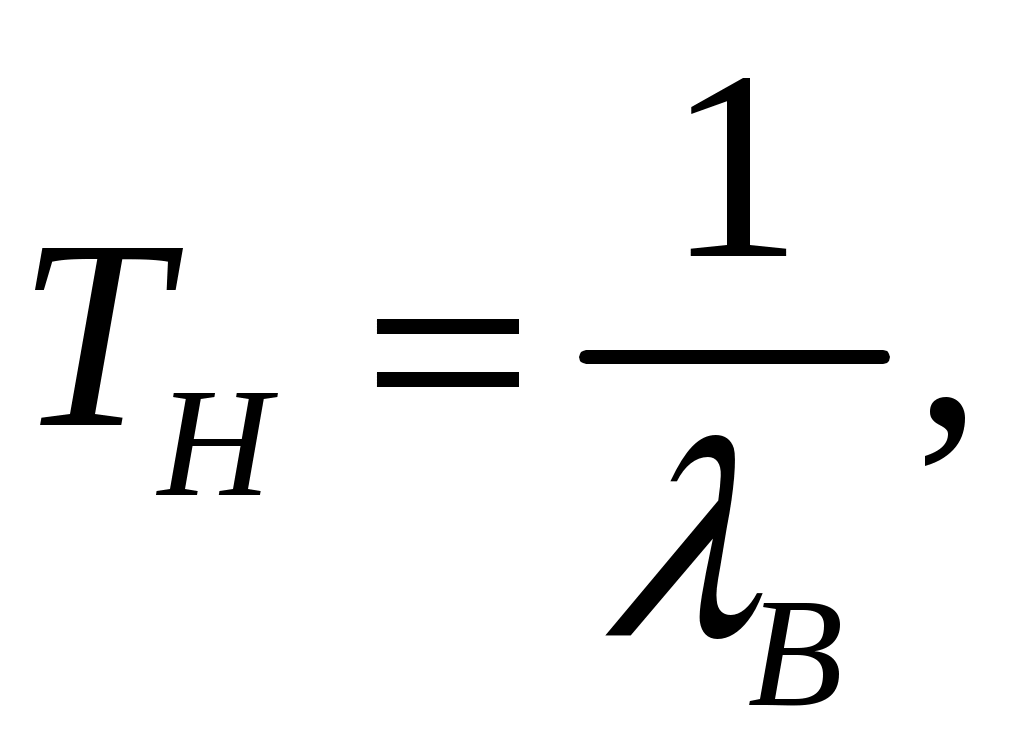
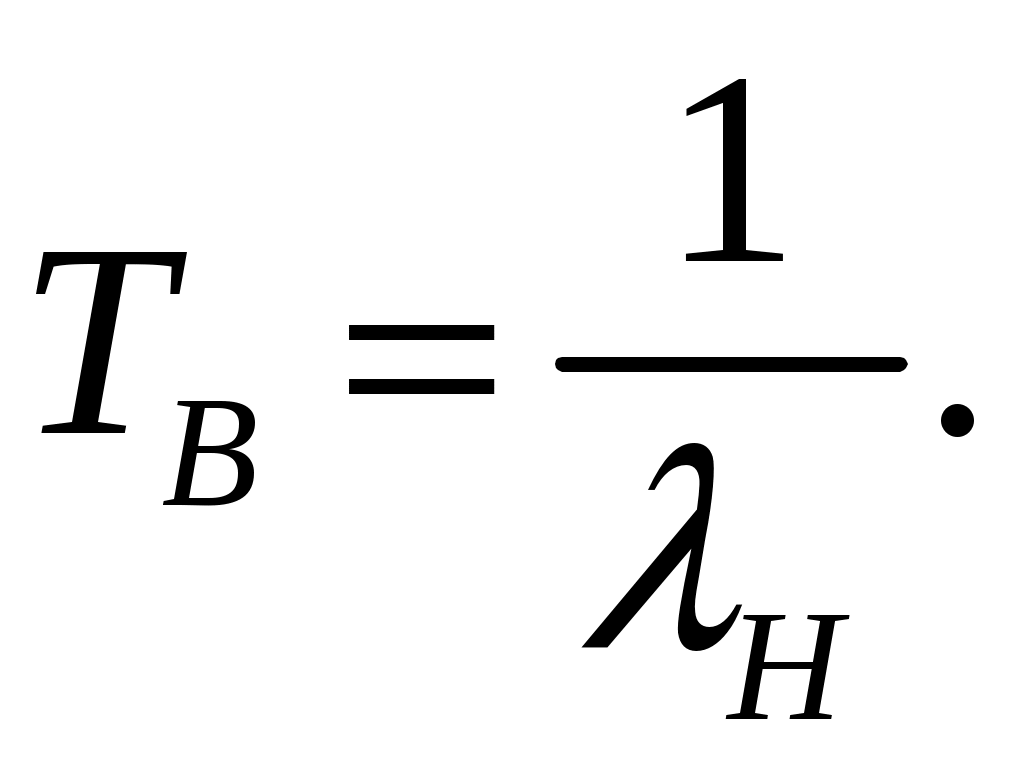 (4.4)
(4.4)Для этих целей можно воспользоваться табл. 3.1 /2/, а значения квантилей
Если число степеней свободы
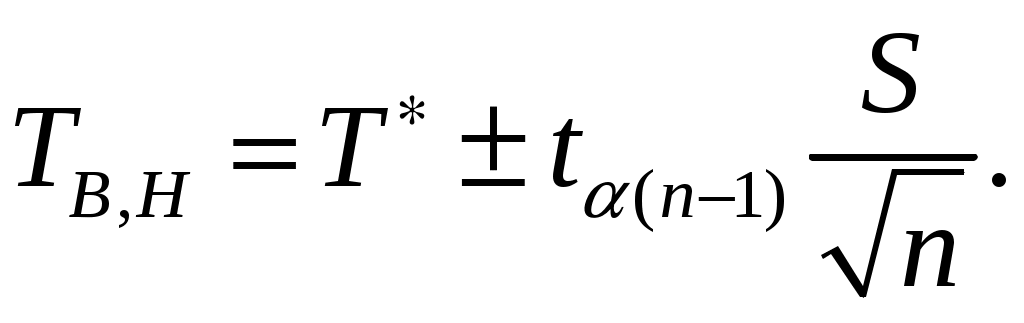
(4.5)
где
Определение значения