Министерство образования Республики Беларусь

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет компьютерных систем и сетей

Кафедра информатики

Дисциплина: Методы численного анализа

ОТЧЁТ

к лабораторной работе

на тему

Метод Адамса

Выполнил: студент группы 153503

Кончик Денис Сергеевич

Проверил: Анисимов Владимир Яковлевич

Минск 2022

Содержание

1. 
   ЦЕЛЬ РАБОТЫ
   

Изучить решение задачи Коши для обыкновенных дифференциальных уравнений методом Адамса.

2. 
   ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
   

3. АЛГОРИТМ РЕШЕНИЯ

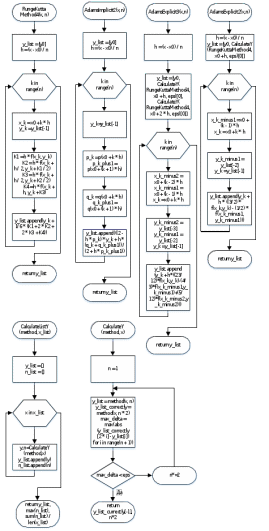
4. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ

# -*- coding: cp1251 -*-

import numpy as np

import matplotlib.pyplot as plt

import sympy

import math
from calculate import CalculateListY

from calculate import CalculateY

plot_dots = 10**3

eps = 10**-3

# Тестовый пример 1

# y'= y + e^x

# y = x * e^x

x0, y0 = 1, math.e

L, R = 1, 2
def f(x, y):

return y + math.e ** x
def p(x):

return -1

def q(x):

return math.e ** x
def ans(x):

return round(x * math.e ** x, 6)

# Метод Рунге-Кутта 4 порядка

def RungeKuttaMethod4(x, n):

y_list = [y0]

h = (x - x0) / n

for k in range(n):

x_k = x0 + k * h

y_k = y_list[-1]

K1 = h * f(x_k, y_k)

K2 = h * f(x_k + h / 2, y_k + K1 / 2)

K3 = h * f(x_k + h / 2, y_k + K2 / 2)

K4 = h * f(x_k + h, y_k + K3)

y_list.append(y_k + 1/6 * (K1 + 2 * K2 + 2 * K3 + K4))

return y_list
# Неявный метод Адамса 2 порядка

def AdamsImplicit2(x, n):

y_list = [y0]

h = (x - x0) / n

for k in range(n):

y_k = y_list[-1]

p_k = p(x0 + k * h)

p_k_plus1 = p(x0 + (k + 1) * h)

q_k = q(x0 + k * h)

q_k_plus1 = q(x0 + (k + 1) * h)

y_list.append(((2 - h * p_k) * y_k + h * (q_k + q_k_plus1)) / (2 + h * p_k_plus1))

return y_list

# Явный метод Адамса 2 порядка

def AdamsExplicit2(x, n):

h = (x - x0) / n

y_list = [y0, CalculateY(RungeKuttaMethod4, x0 + h, eps)[0]]

for k in range (1, n):

---

x_k_minus1 = x0 + (k - 1) * h

x_k = x0 + k * h

y_k_minus1 = y_list[-2]

y_k = y_list[-1]

y_list.append(y_k + h * ((3/2) * f(x_k,y_k) - (1/2) * f(x_k_minus1, y_k_minus1)))

return y_list

# Явный метод Адамса 3 порядка

def AdamsExplicit3(x, n):

h = (x - x0) / n

y_list = [y0, CalculateY(RungeKuttaMethod4, x0 + h, eps)[0], CalculateY(RungeKuttaMethod4, x0 + 2 * h, eps)[0]]

for k in range (2, n):

x_k_minus2 = x0 + (k - 2) * h

x_k_minus1 = x0 + (k - 1) * h

x_k = x0 + k * h

y_k_minus2 = y_list[-3]

y_k_minus1 = y_list[-2]

y_k = y_list[-1]

y_list.append(y_k + h*((23/12)*f(x_k,y_k)-(4/3)*f(x_k_minus1,y_k_minus1)+(5/12)*f(x_k_minus2,y_k_minus2)))

return y_list

x_list = []

for i in range(plot_dots + 1):

x_list.append(L + (R - L) / plot_dots * i)

xToCalculate = 1.5

print(f"Количество точек для построения графика: {plot_dots}")

print(f"Точность: {eps:.0e}")

print("\nN_max – максимальное количество узлов для одной из точек, \nнеобходимое для достижения заданной точности")

print("N_middle – среднее количество узлов по всем точкам при \nдостижении заданной точности")
print(f"\nТочка: {xToCalculate}")

print(f"Калькулятор: {ans(xToCalculate)}")
y_list, N_max, N_middle = CalculateListY(AdamsImplicit2, x_list, eps)

print("\nНеявный метод Адамса 2 порядка O(h^2):")

print(f"N_max: {N_max}")

print(f"N_middle: {int(N_middle)}")

print("На графике: красный")

print(f"В точке: {CalculateY(AdamsImplicit2, xToCalculate, eps)[0]} [{CalculateY(AdamsImplicit2, xToCalculate, eps)[1]}]")

print(f"Delta = {abs(CalculateY(AdamsImplicit2, xToCalculate, eps)[0] - ans(xToCalculate)):.2e}")

plt.plot(x_list, y_list, 'red', linewidth = 2)
y_list, N_max, N_middle = CalculateListY(AdamsExplicit2, x_list, eps)

print("\nЯвный метод Адамса 2 порядка O(h^2):")

print(f"N_max: {N_max}")

print(f"N_middle: {int(N_middle)}")

print("На графике: синий")

print(f"В точке: {CalculateY(AdamsExplicit2, xToCalculate, eps)[0]} [{CalculateY(AdamsExplicit2, xToCalculate, eps)[1]}]")

print(f"Delta = {abs(CalculateY(AdamsExplicit2, xToCalculate, eps)[0] - ans(xToCalculate)):.2e}")

plt.plot(x_list, y_list, '--b', linewidth = 2)
y_list, N_max, N_middle = CalculateListY(AdamsExplicit3, x_list, eps)

print("\nЯвный метод Адамса 3 порядка O(h^3):")

print(f"N_max: {N_max}")

print(f"N_middle: {int(N_middle)}")

print("На графике: желтый")

print(f"В точке: {CalculateY(AdamsExplicit3, xToCalculate, eps)[0]} [{CalculateY(AdamsExplicit3, xToCalculate, eps)[1]}]")

print(f"Delta = {abs(CalculateY(AdamsExplicit3, xToCalculate, eps)[0] - ans(xToCalculate)):.2e}")

plt.plot(x_list, y_list, ':y', linewidth = 2)
plt.show()


# Вычислить Y по методу и X

def CalculateY(method, x, eps):

n = 1 # Количество узлов от x0 до x для точности eps
while True:

y_list = method(x, n)

y_list_correctly = method(x, n * 2)

max_delta = max(abs(y_list_correctly[2 * i] - y_list[i]) for i in range(n + 1))
if (max_delta < eps):

return round(y_list_correctly[-1], 6), n * 2

else:

n *= 2
# Создать список Y по методу и списку X

def CalculateListY(method, x_list, eps):

y_list = [] # Список игреков

n_list = [] # Список n (числа узлов) для каждой точки

for x in x_list:

y, n = CalculateY(method, x, eps)

y_list.append(y)

n_list.append(n)
return y_list, max(n_list), sum(n_list) / len(x_list)

5. ТЕСТОВЫЕ ПРИМЕРЫ

Явные методы Адамса k-го порядка требуют предварительного вычисления решения в k начальных точках. Для вычисления начальных значений программа использует метод Рунге-Кутта 4-го порядка.

---

Для неявного метода Адамса 2-го порядка программа считает, что исходное дифференциальное уравнение является линейным.
Тестовый пример 1.1.

С помощью неявного метода Адамса 2 порядка¹, явных методов Адамса 2, 3, 4 порядков^2,3,4 найти с заданной точностью решение заданного уравнения на заданном отрезке.

ДУ	Начальное условие		Отрезок	Решение		Точность
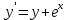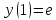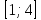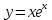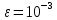Точек для построения графиков: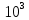
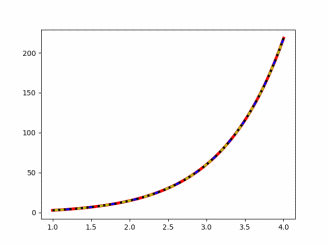1 – красный, 2 – синий, 3 – желтый, 4 – черный
Количество необходимых для достижения заданной точности точек разбиения отрезка для одной из точек в методе
	Адамс [2] (неявный)	Адамс [2] (явный)			Адамс [3] (явный)		Адамс [4] (явный)
Макс.	2048	4096			512		256
Ср.	556	1228			190		71

---

Тестовый пример 1.2.

Для условия предыдущего задания найти значения решения задачи Коши в заданных точках.

n – число точек разбиения отрезка [1; x] для достижения заданной точности 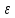в точке x.

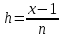– шаг разбиения, соответствующий количеству точек разбиения n.

Неявный метод Адамса 2-го порядка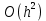
x	2.0	2.7	3.4
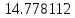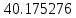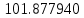Метод(х)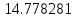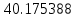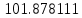
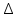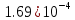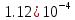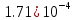n	128	512	1024

---

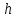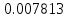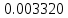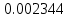Явный метод Адамса 2-го порядка
x	2.0	2.7	3.4
Метод(х)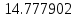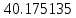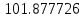
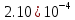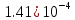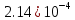n	256	1024	2048

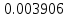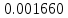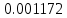Явный метод Адамса 3-го порядка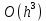
x	2.0	2.7	3.4
Метод(х)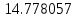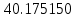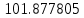
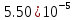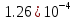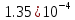n	64	128	256

---

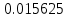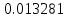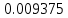Смотрите также файлы

• Задание 3. Тема Экспертиза качества непродовольственных товаров. Идентификация непродовольственных товаров.docx

• Тема Методические аспекты взаимосвязи стратегического и проектного управления в предпринимательской деятельности.docx

• Методические указания по выполнению практических работ по дисциплине математика для студентов направления подготовки 43. 03. 03 Гостиничное дело Направленность (профиль) Гостиничная деятельность.pdf

• 12 недель в году. Как за 12недель сделать больше, чемдругие успевают за 12 месяцев.pdf

• Методические указания к практическим занятиям.docx