ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.12.2023
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тестовый пример 3.2.
Для условия предыдущего задания найти значения решения задачи Коши в заданных точках.
n – число точек разбиения отрезка [1; x] для достижения заданной точности
в точке x.
– шаг разбиения, соответствующий количеству точек разбиения n.| Неявный метод Адамса 2-го порядка  | |||
| x | 2.0 | 3.5 | 5.0 |
| y = -1/x |  |  |  |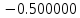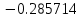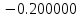
| Метод(х) |  |  |  |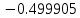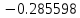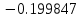
 |  |  |  |
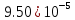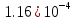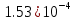| n | 64 | 256 | 512 |
 |  |  |  |
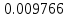| Явный метод Адамса 2-го порядка | |||
| x | 2.0 | 3.5 | 5.0 |
| y = -1/x |  |  |  |
| Метод(х) |  |  |  |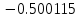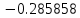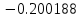
| |  |  |  |
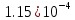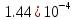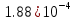| n | 128 | 512 | 1024 |
| | |  |  |
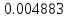| Явный метод Адамса 3-го порядка  | |||
| x | 2.0 | 3.5 | 5.0 |
| y = -1/x | | | |
| Метод(х) |  |  |  |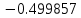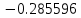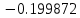
| |  |  |  |
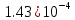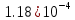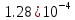| n | 32 | 128 | 256 |
| |  |  |  |
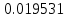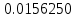| Явный метод Адамса 4-го порядка  | |||
| x | 2.0 | 3.5 | 5.0 |
| y = -1/x | | | |
| Метод(х) |  |  |  |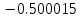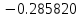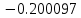
| |  |  |  |
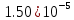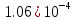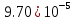| n | 32 | 64 | 128 |
| | |  | |
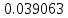6. ЗАДАНИЕ
Вариант 11
Найти с точностью до 0.001 решение уравнения на отрезке [0; 1].
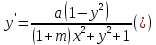
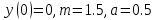
| ДУ | Начальное условие | Отрезок | Точность | ||
 |  |  |  | ||
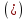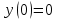| Точек для построения графиков:  | |||||
 | |||||
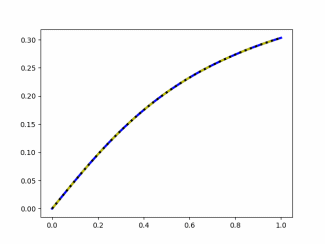| Цвета графиков, построенных явными методами: Адамс [2] – синий, Адамс [3] – желтый, Адамс [4] – черный | |||||
| Количество необходимых для достижения заданной точности точек разбиения отрезка для одной из точек в методе | |||||
| | Адамс [2] (явный) | Адамс [3] (явный) | Адамс [4] (явный) | ||
| Макс. | 32 | 32 | 16 | ||
| Ср. | 16 | 9 | 6 | ||
7. ВЫВОД
Таким образом, в ходе выполнения лабораторной работы был изучены методы Адамса для решения задачи Коши ОДУ 1 порядка. Составлен алгоритм и программа, проверена правильность её работы на тестовых примерах, с заданной точностью построены графики решения задачи Коши.
Исходя из тестовых примеров и задания и учитывая количество необходимых точек разбиения отрезка для достижения заданной точности, можно сделать вывод о трудоемкости методов: методы Адамса (явный и неявный) 2-го порядка более трудоемкие по сравнению с методами 3-го и 4-го порядка (явные). Самым эффективным оказался явный метод Адамса 4-го порядка.