Упростим выражение:

Упростим следующее выражение:



Интеграл принимает вид:



Продолжим преобразование подынтегрального выражения:



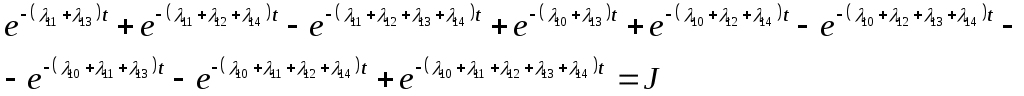
Интеграл вида имеет первообразную:



Учитывая полученный результат определим :



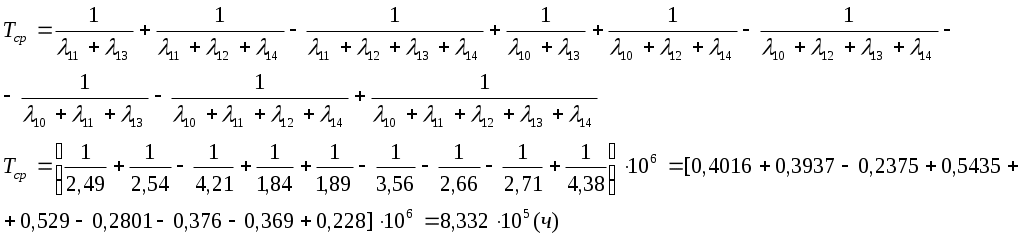
Определим интенсивность отказов узла I:



Частота отказов узла системы может быть найдена по формуле:














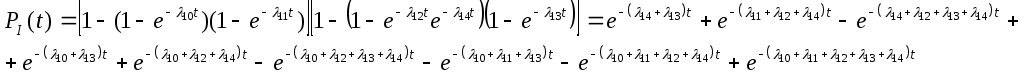
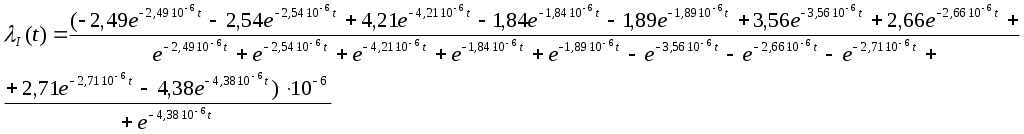
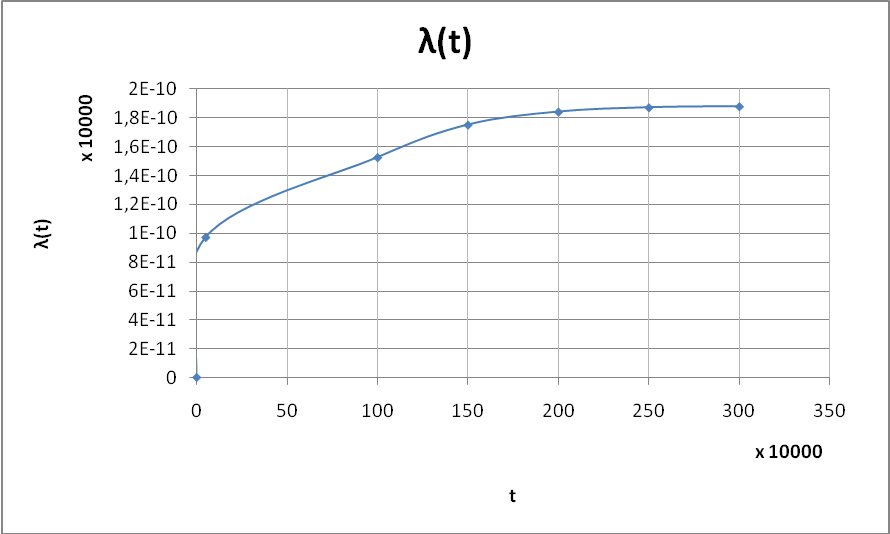
Задача №3.2.
Система содержит n групп элементов, каждая j – группа, в свою очередь, содержит N_j элементов, причем λ_j – интенсивность отказов элементов j – группы. Вероятность безотказной работы системы за время t равна Р_к(t). Требуется определить число элементов ЗИПа. Исходные данные приведены в таблице.

№ Вар	Рк(t)	t,ч	n	Реле		Резисторы		Конденсаторы		Диоды		Транзисторы
				N1	λ1*10-5	N2	λ2*10-5	N3	λ3*10-6	N4	λ4*10-6	N5	λ5*10-6
22	0,92	17000	5	20	1,4	36	0,2	36	1,6	28	2,5	40	0,95

---

Определим интенсивности отказов групп элементов:


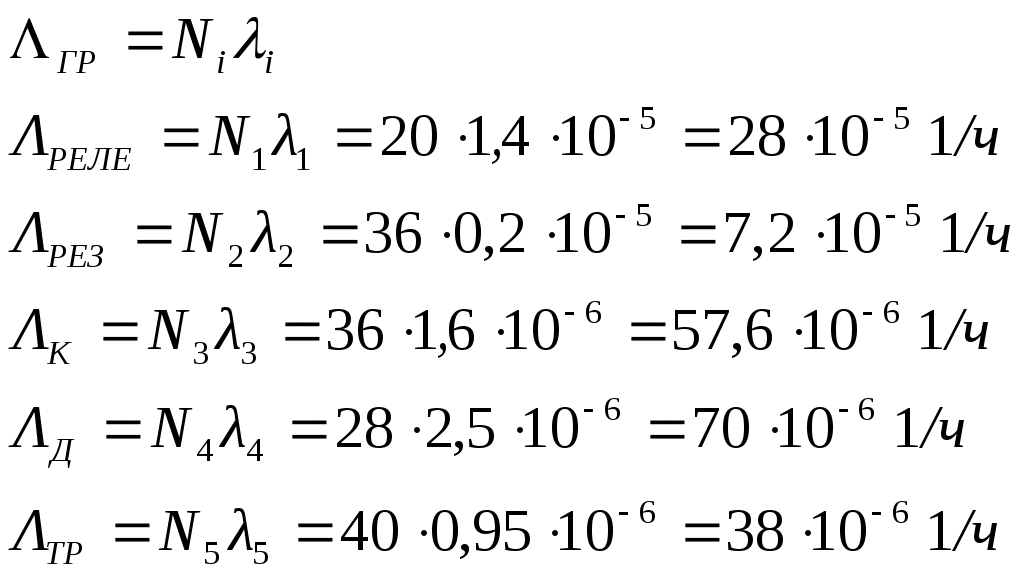
Определим вероятность безотказной работы групп элементов:



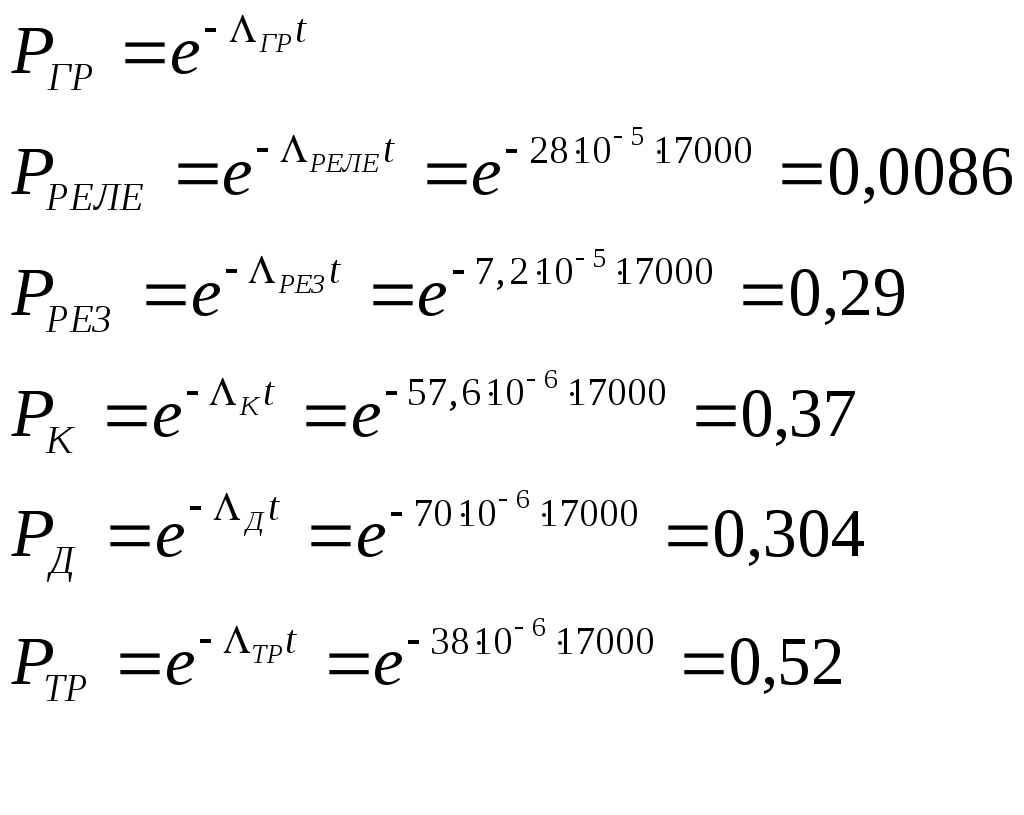
Определим вероятность безотказной работы системы при последовательном соединении без ЗИПа:



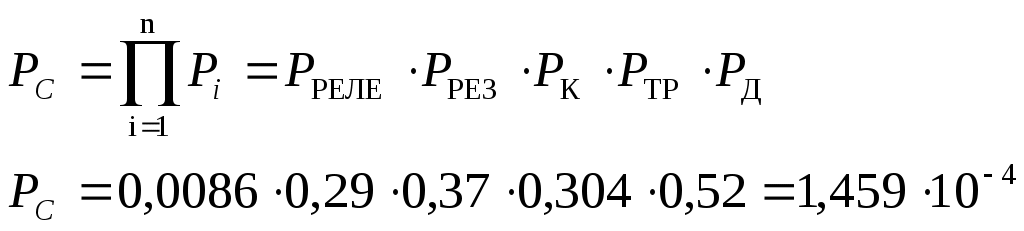
Определим коэффициент ЗИПа:



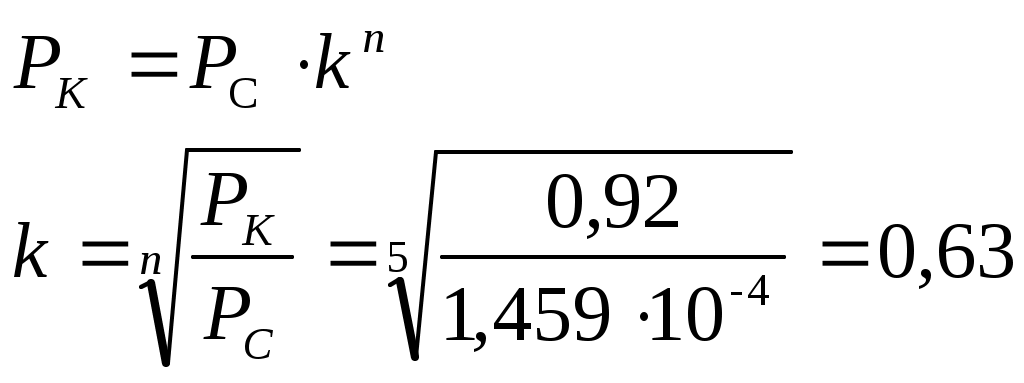
Для холодного ЗИПа справедливо выражение:



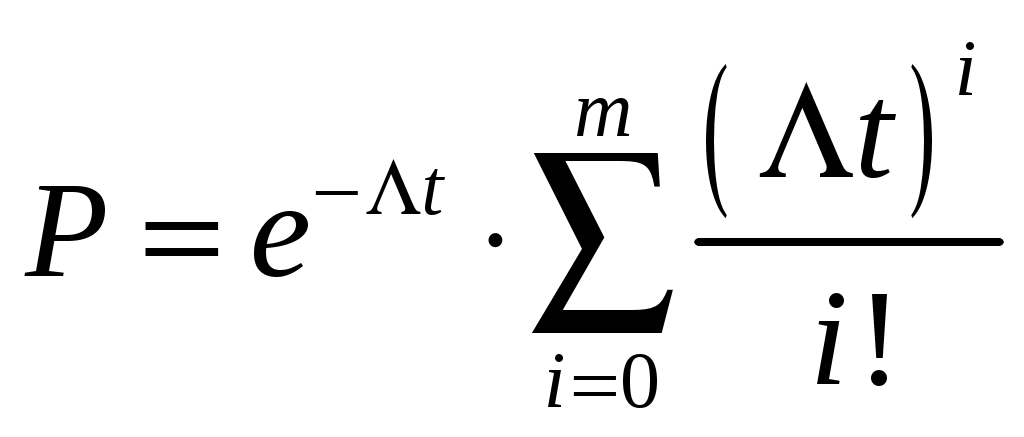
_{Число запасных элементов m определяется подбором, при условии}


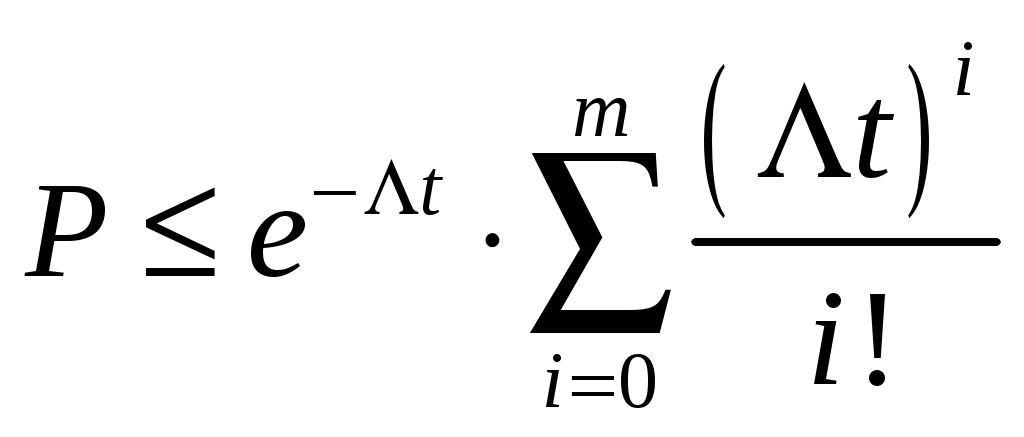
Определим число элементов ЗИПа для реле:



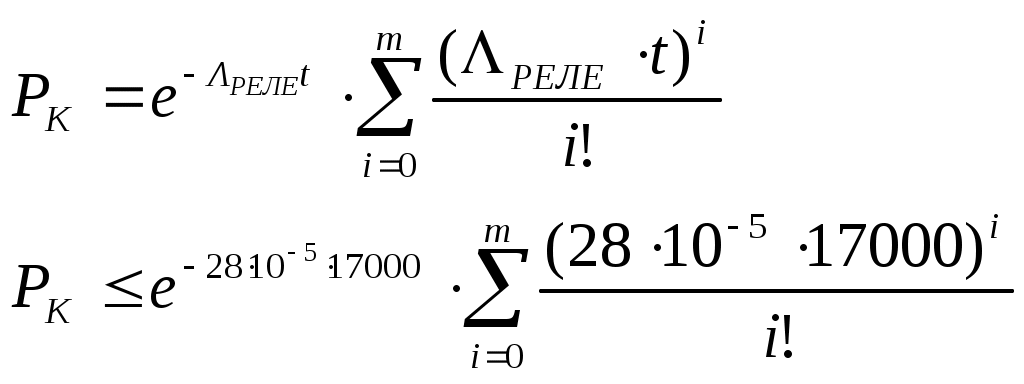
Подбором установлено m≥8


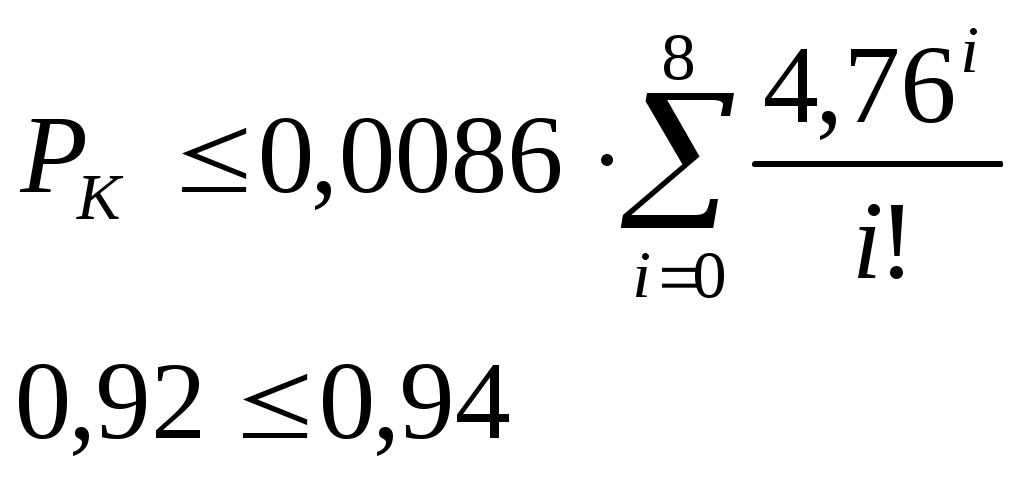
Определим число элементов ЗИПа для резисторов:



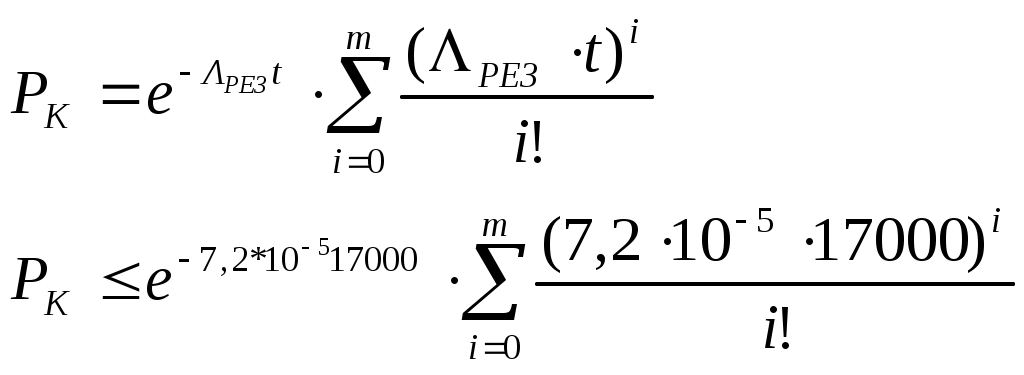
Подбором установлено m≥3



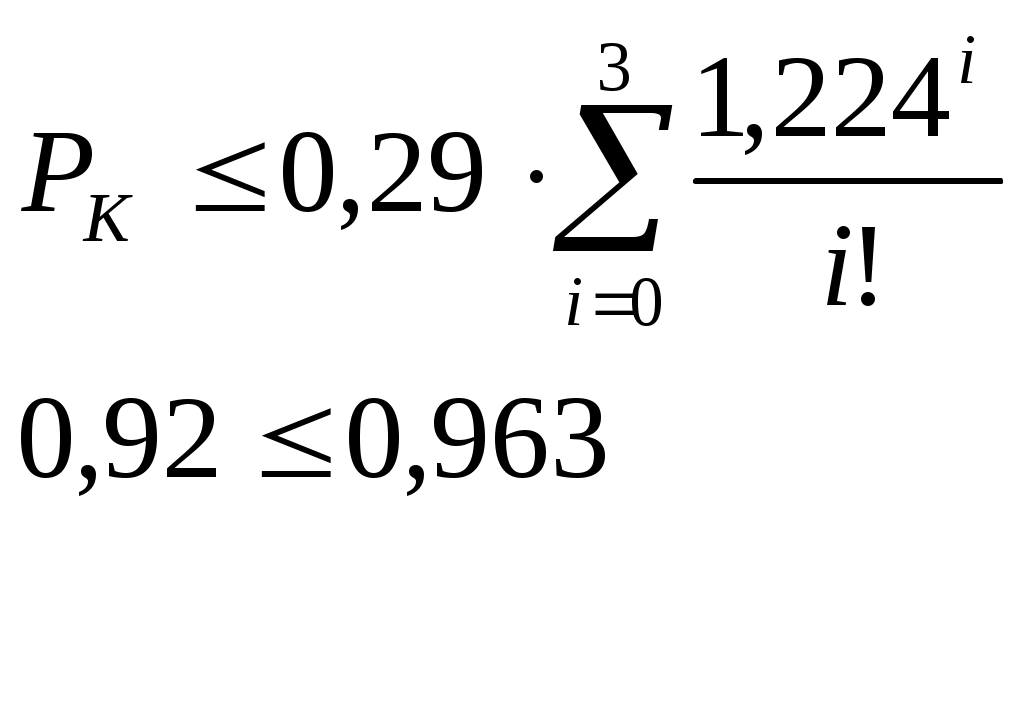
Определим число элементов ЗИПа для конденсаторов:



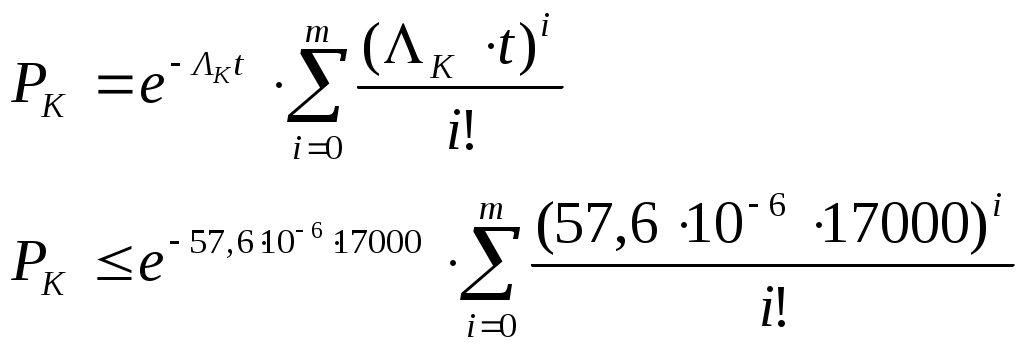
Подбором установлено m≥2


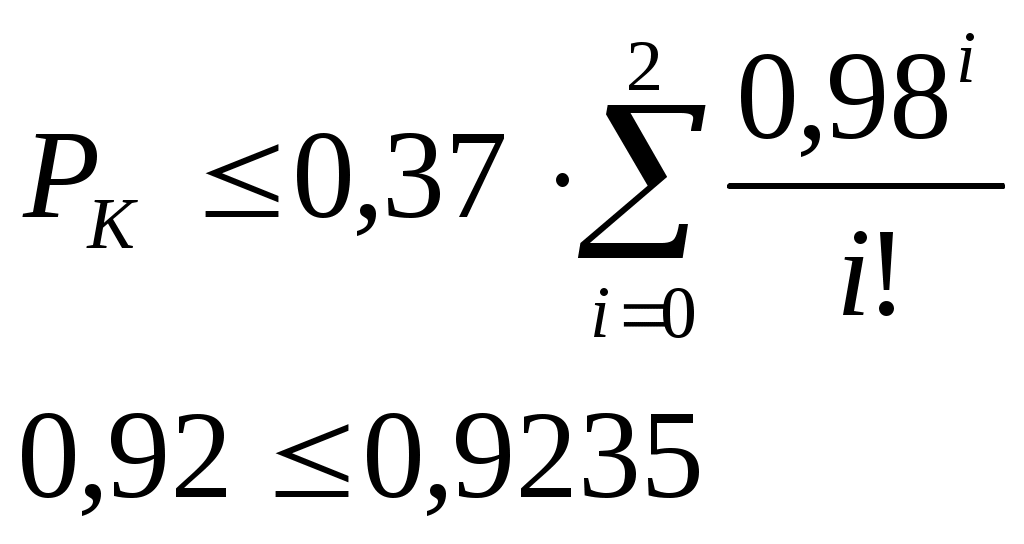
Определим число элементов ЗИПа для диодов:


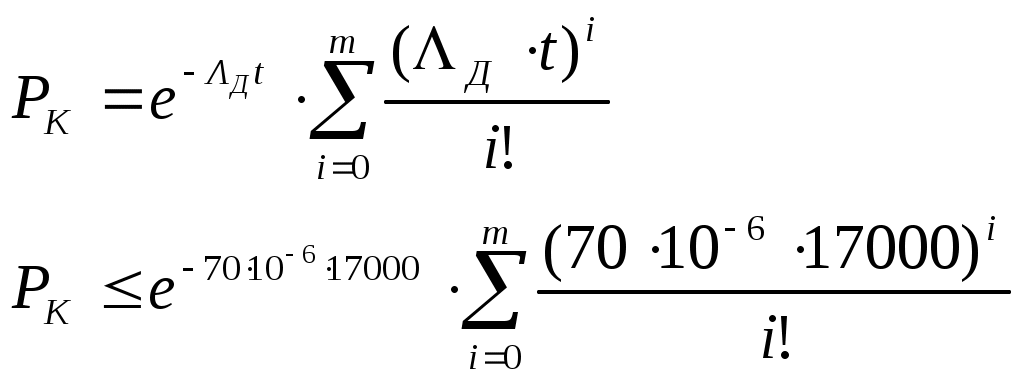
Подбором установлено m≥3



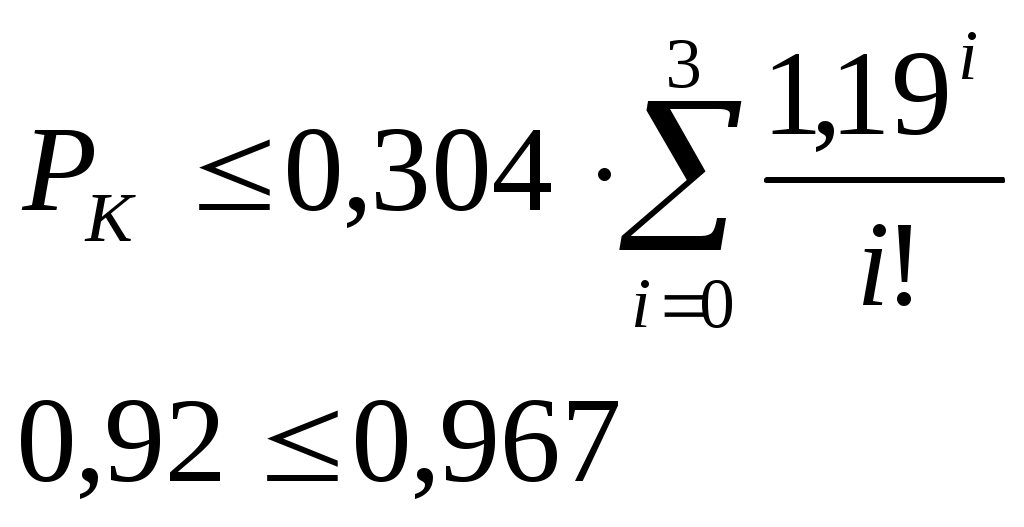
Определим число элементов ЗИПа для транзисторов:



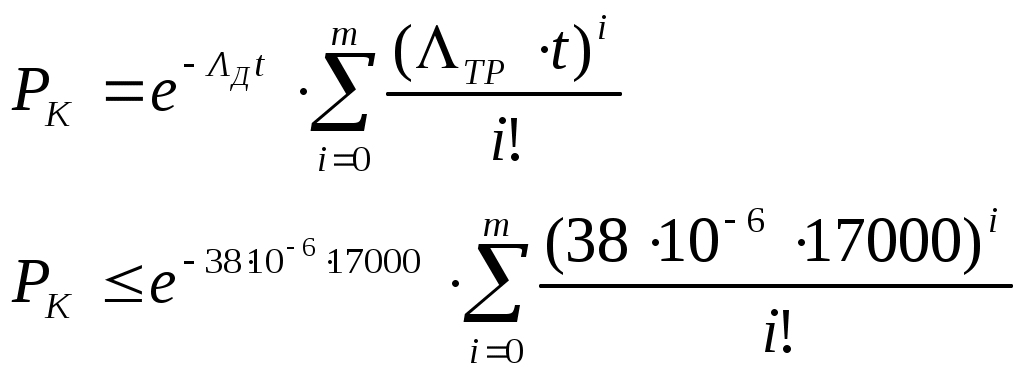
Подбором установлено m≥2




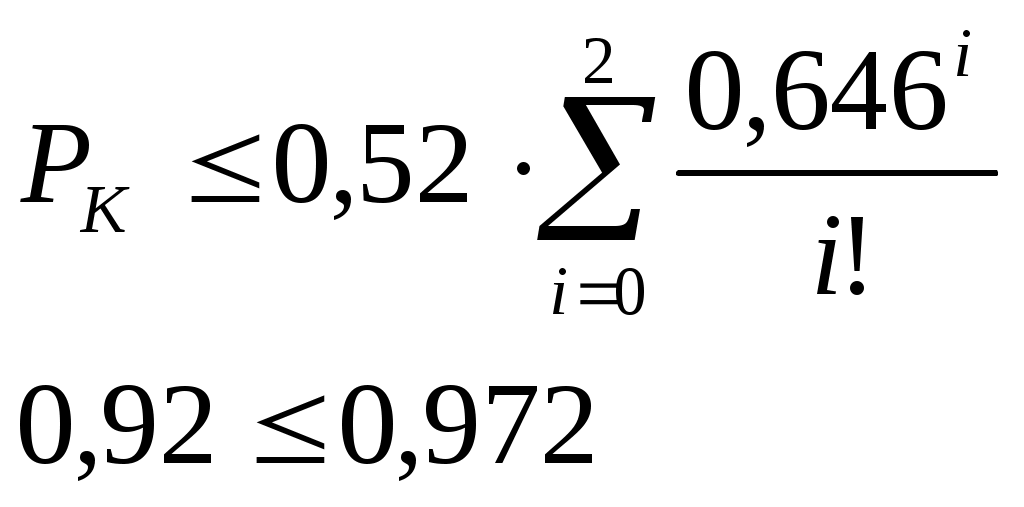
Задача №4.1.22.
В результате испытания 11-ти редукторов, отказы которых распределены нормально

---

, получены следующие значения времени безотказной работы в часах: t₁=1500, t₂=1000, t₃=700, t₄=2000, t₅=1050, t₆=1000, t₇=1600, t₈=1900, t₉=800, t₁₀=1500, t₁₁=1850.

Требуется оценить Т и σ и определить для них двухсторонние интервалы с вероятностью α=0,95.

Решение

Для построения статистического ряда время испытаний разобьем на 10 интервалов (разрядов) продолжительностью 200 ч и для каждого разряда подсчитаем Q^*(t), λ^*(t), f^*(t).

Параметр	Разряды
	1	2	3	4	5	6	7	8	9	10
n*	0	0	0	2	2	1	0	3	0	3
f*·1031/ч	0	0	0	0,909	0,909	0,455	0	1,364	0	1,364
λ*1031/ч	0	0	0	1	1,25	0,769	0	3,33	0	10
Q*(t)	0	0	0	0,182	0,364	0,455	0,455	0,73	0,73	1
λэ1031/ч	0,67	0,67	0,67	0,67	0,67	0,67	0,67	0,67	0,67	0,67
fэ·1031/ч	0,586	0,512	0,448	0,398	0,342	0,302	0,26	0,236	0,2	0,17
Qэ	0,1254	0,235	0,331	0,415	0,488	0,552	0,608	0,657	0,7	0,74
qi	0	0	0	0,182	0,364	0,455	0,455	0,73	0,73	1
Uqi	-3,89	-3,89	-3,89	-0,84	-0,38	-0,1257	-0,1257	0,523	0,523	3,89
fн·1031/ч	0,0383	0,1	0,227	0,42	0,64	0,814	0,857	0,747	0,54	0,32
Рн	0,9936	0,9803	0,9474	0,883	0,7794	0,6293	0,4602	0,3015	0,1685	0,0823
Qн	0,0064	0,0197	0,0526	0,117	0,2206	0,3707	0,5398	0,6985	0,8315	0,9177
λн·1031/ч	0,0386	0,104	0,24	0,47	0,82	1,29	1,86	2,48	3,21	3,95
qi	0,1254	0,109	0,095	0,084	0,073	0,064	0,056	0,049	0,042	0,0375
qiн	0	0,0004	0,015	0,0142	0,0894	0,2501	0,3358	0,2247	0,0718	0,0111
λ2iн	0,0044	0,0044	0,0165	21,764	1,05	1,11	3,69	0,113	0,79	67,83
λ2iэ	1,37	1,199	1,045	1,253	1,784	0,1244	0,616	11,24	0,462	16,23

---

Поскольку за время испытаний отказали все изделия (100%), то оценка интенсивности отказов подсчитывалась с использованием выражения, приведенного для плана N, Б, ч (считая, что испытания прекратились после 11-го отказа).





Т.к. в данном случае N=r=1, то:





Частота отказов определялась для каждого разряда из выражения:



Вероятность отказа:
Если испытания проводились до отказа всех изделий, то оценка математического ожидания и среднеквадратичного отклонения могут быть определены из выражения:







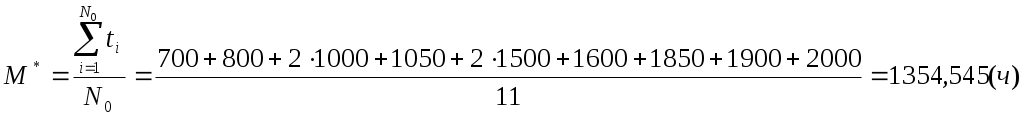
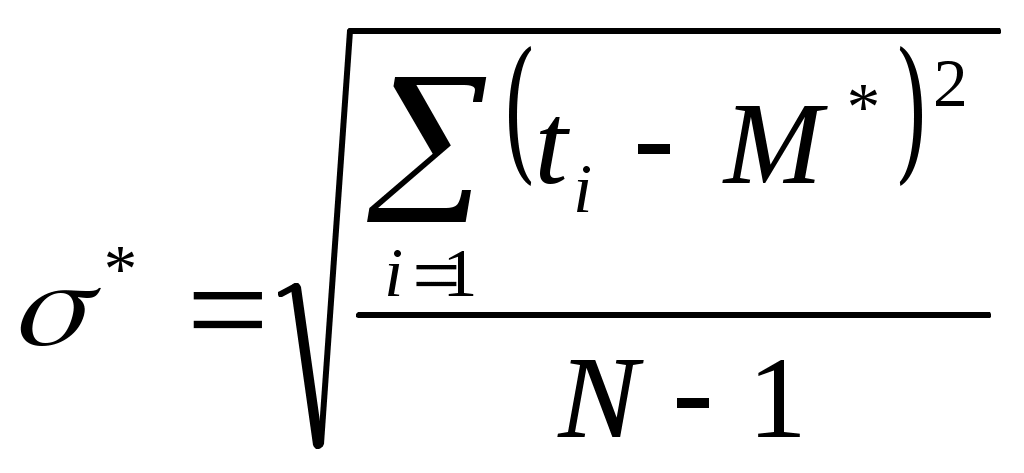
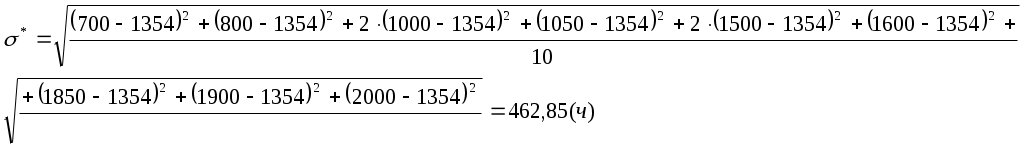
Для определения математического ожидания и среднеквадратичного отклонения для каждого разряда подсчитаем

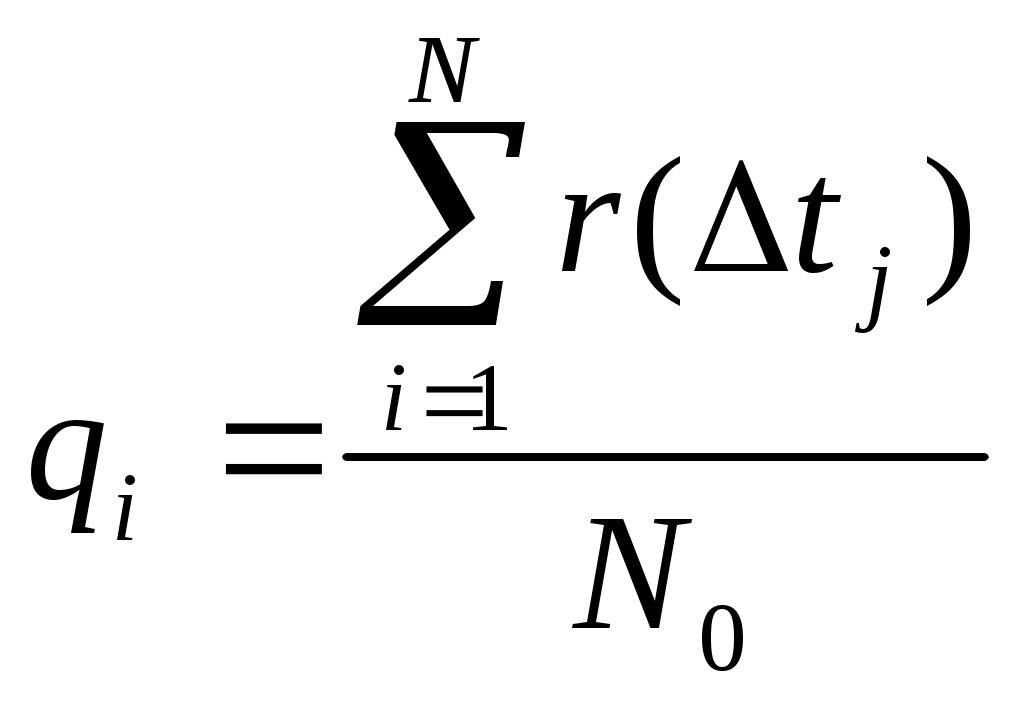
Для каждого разряда составим уравнение и эти уравнения сложим:

200=M-3,896 σ

400=М-3,896 σ

600=М-3,896 σ

800=М-0,846 σ

1000=М-0,386 σ

1200=М-0,1258 σ

1400=М-0,1258 σ

1600=М+0,5236 σ

1800=М+0,5236 σ

2000=М+3,896 σ ___

11000=10·М-8,205 σ
Полученные новые уравнения умножаем на соответствующий квантиль:

-778=-3,89М+15,132 σ

-1556=-3,89М+15,132 σ

-2334=-3,89М+15,132 σ

-672=-0,84М+0,706 σ

-380=-0,38М+0,1445 σ

-150,84=-0,1275М+0,0159 σ

-175,98=-0,1257М+0,0159 σ

836,8=0,523М+0,275 σ

---

941,4=0,523М+0,275 σ

7780=3,89М+15,135 σ ___

3511,38=-8,2М+61,95 σ

Решаем совместно уравнения:

1 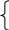0М-8,205σ=11000

-8,2М+61,95 σ=3511,38

Получаем: М=1286ч, σ=227ч

Для каждого разряда подсчитаем частоту, интенсивность и вероятность отказа:



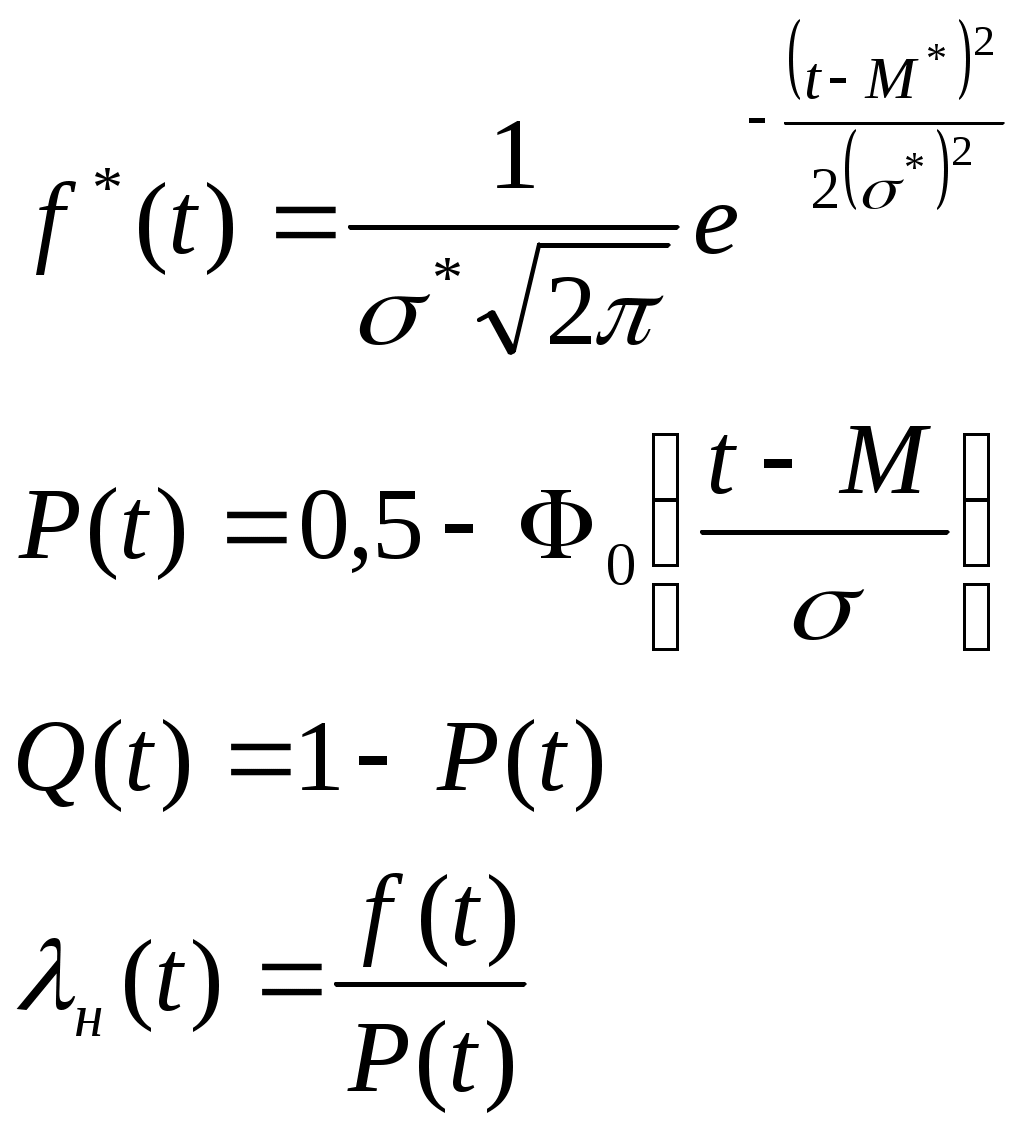
Для определения доверительных интервалов при экспоненциальном законе распределения по таблице квантилей.

квадрат распределений

найдем где 2r=20

при

при

Суммарная наработка всех изделий

Для плана N, Б, r определим



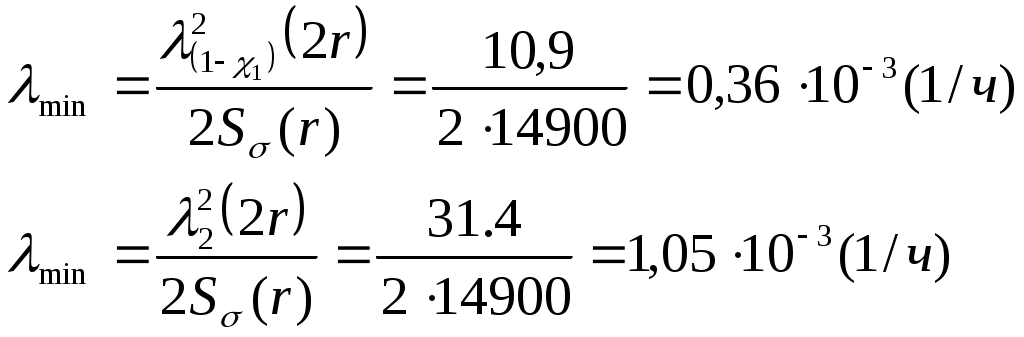
Тысячная оценка интенсивности попала в доверительный интервал.

Для определения доверительного интервала для математического ожидания найдем по таблице квантилей распределения Стьюдента квантиль вероятности 0,05 при девяти степенях свободы:

t_α=2,262



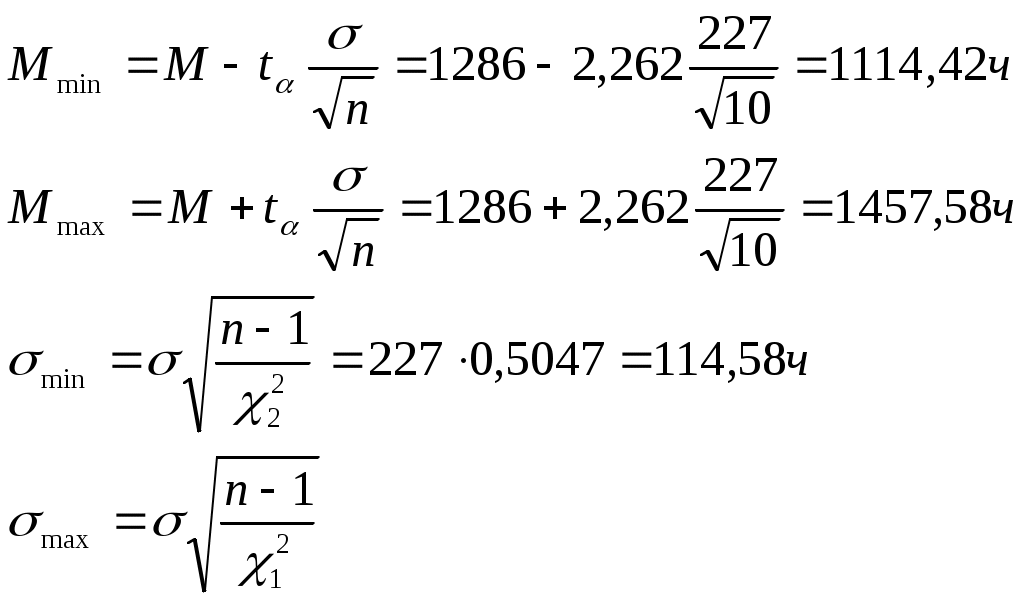
Для определения доверительного интервала для среднеквадратичного отклонения по таблице квантилей для вероятностей P₁=0,05 и Р₂=0,95 при девяти степенях свободы.

---

Смотрите также файлы

• Уловки в спора.docx

• Типовое задание к дидактической игре.docx

• Инвестиционный анализ контрольная работа.doc

• XI. система прерываний компьютера. Основные понятия.doc

• Цезарь Антонович Кюи.docx