ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 323
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2 ВАРИАНТ
| Оценивание заданий работы | ||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество баллов | 1 | 1 | 4 | 4 | 5 | 5 |
| Всего баллов | 20 баллов | |||||
1. Найдите количество сторон правильного многоугольника, если сумма всех его внутренних углов равна 1980°.
А) 18 В) 13 С) 12 D) 11
2. Дана окружность радиуса 12 см . Чему равна длина ее дуги с градусной мерой 90°?
А) 4 см В) 6 см С) 8 см D) 12 см
3. Три угла четырехугольника, вписанного в окружность, взятые в порядке следования, относятся как 2 : 6 : 7. Найдите углы четырехугольника.
4. В окружность вписан квадрат со стороной 4√2 см. Найдите площадь правильного треугольника, описанного около этой окружности.
5. Основание АВ треугольника АВС равно 26 см. Медианы АК и ВМ, проведенные к боковым сторонам, равны соответственно 30 см и 39 см. Найдите площадь треугольника АВС.

6. На рисунке изображен сектор круга с центром в точке O и радиусом, равным 8 см. ОD = 2 см и DOС 45°. Найдите площадь закрашенной области.

Схема выставления баллов
2 вариант
| № | Ответ | Балл | Дополнительная информация |
| 1 | B | 1 | |
| 2 | B | 1 | |
| 3 | 2х + 7х = 180° | 1 | |
| х = 20° | 1 | | |
| 40°, 120°, 140° | 1 | | |
| 180° – 120° = 60° | 1 | | |
| 4 | | 1 | |
| | 1 | Принимается альтернативное решение | |
| | 1 | | |
| | 1 | | |
| 5 | АО=2х, ОК=х 2х х 30 или ВО=2х,ОМ=х 2х х 39 | 1 | Применяет свойство медиан треугольника |
| АО = 20 см и ВО = 26 см | 1 | | |
| Полупериметр | 1 | | |
| | 1 | | |
| SABC 3240 720 см2 | 1 | Применяет свойство медиан треугольника | |
| 6 | | 1 | |
| DC=DOsin450 | 1 | Принимается альтернативное решение | |
| | 1 | | |
| | 1 | | |
| | 1 | | |
| Итого: | 20 | | |
3 ВАРИАНТ
| Оценивание заданий работы | ||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество баллов | 1 | 1 | 4 | 4 | 5 | 5 |
| Всего баллов | 20 баллов | |||||
1. Найдите количество сторон правильного многоугольника, если сумма всех его внутренних углов равна 1440°.
А) 8 В) 9 С) 10 D) 12
2. Дана окружность радиуса 12 см . Чему равна длина ее дуги с градусной мерой 90°?
А) 4 см В) 6 см С) 8 см D) 12 см
3. Сумма углов выпуклого многоугольника на 7200больше суммы его внешних углов, взятых по одному при каждой вершине. Найдите число сторон этого многоугольника
4. В окружность вписан квадрат со стороной 4 √2 см. Найдите площадь правильного треугольника, описанного около этой окружности.
5. Основание АВ треугольника АВС равно 26 см. Медианы АК и ВМ, проведенные к боковым сторонам, равны соответственно 30 см и 39 см. Найдите площадь треугольника АВС.

6. На рисунке изображен сектор круга с центром в точке O и радиусом, равным 6 см. ОD = 2 см и DOС 45°. Найдите площадь закрашенной области.
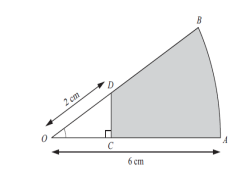
Схема выставления баллов
3 вариант
| № | Ответ | Балл | Дополнительная информация |
| 1 | С | 1 | |
| 2 | B | 1 | |
| 3 | 180(n-2)=3600+7200 | 1 | |
| n-2=10800:1800 | 1 | | |
| n-2=6 | 1 | | |
| n=8 | 1 | | |
| 4 | | 1 | |
| | 1 | Принимается альтернативное решение | |
| | 1 | | |
| | 1 | | |
| 5 | АО=2х, ОК=х 2х х 30 или ВО=2х,ОМ=х 2х х 39 | 1 | Применяет свойство медиан треугольника |
| АО = 20 см и ВО = 26 см | 1 | | |
| Полупериметр | 1 | | |
| | 1 | | |
| SABC 3240 720 см2 | 1 | Применяет свойство медиан треугольника | |
| 6 | | 1 | |
| DC=DOsin450 | 1 | Принимается альтернативное решение | |
| | 1 | | |
| | 1 | | |
| | 1 | | |
| Итого: | 20 | | |
4 ВАРИАНТ
| Оценивание заданий работы | ||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество баллов | 1 | 1 | 4 | 4 | 5 | 5 |
| Всего баллов | 20 баллов | |||||
1. Найдите количество сторон правильного многоугольника, если сумма всех его внутренних углов равна 1440°.
А) 8 В) 9 С) 10 D) 12
2. Дана окружность радиуса 12 см . Чему равна длина ее дуги с градусной мерой 60°?
А) 4 см В) 6 см С) 8 см D) 12 см
3. Сумма углов выпуклого многоугольника на 9000больше суммы его внешних углов, взятых по одному при каждой вершине. Найдите число сторон этого многоугольника
4. В окружность вписан квадрат со стороной 8√ 2 см. Найдите площадь правильного треугольника, описанного около этой окружности.
5. Основание АВ треугольника АВС равно 26 см. Медианы АК и ВМ, проведенные к боковым сторонам, равны соответственно 30 см и 39 см. Найдите площадь треугольника АВС.

6. На рисунке изображен сектор круга с центром в точке O и радиусом, равным 8 см. ОD = 2 см и DOС 45°. Найдите площадь закрашенной области.
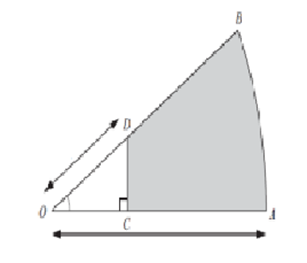
Схема выставления баллов
4 вариант
| № | Ответ | Балл | Дополнительная информация |
| 1 | С | 1 | |
| 2 | А | 1 | |
| 3 | 180(n-2)=3600+9000 | 1 | |
| n-2=12600:1800 | 1 | | |
| n-2=7 | 1 | | |
| n=9 | 1 | | |
| 4 | | 1 | |
| | 1 | Принимается альтернативное решение | |
| | 1 | | |
| | 1 | | |
| 5 | АО=2х, ОК=х 2х х 30 или ВО=2х,ОМ=х 2х х 39 | 1 | Применяет свойство медиан треугольника |
| АО = 20 см и ВО = 26 см | 1 | | |
| Полупериметр | 1 | | |
| | 1 | | |
| SABC 3240 720 см2 | 1 | Применяет свойство медиан треугольника | |
| 6 | | 1 | |
| DC=DOsin450 | 1 | Принимается альтернативное решение | |
| | 1 | | |
| | 1 | | |
| | 1 | | |
| Итого: | 20 | | |
Форма анализа суммативного оценивания за учебный период (четверть)
___________________Педагог:_____________________________________________________________________'>_________________________________________________
(наименование организации образования)
Сведения об анализе по итогам проведения суммативного оценивания
за ______ четверть по предмету _______________
Класс: __________
Количество учащихся: __________________
Педагог: ____________________________________________________________________
Цель: Анализ результатов СОР и СОЧ
| Предмет | Писал | Макс балл | Процентное содержание баллов суммативного оценивания | % качества | |||
| низкий | средний | высокий | |||||
| 0-39% | 40-84% | 85-100% | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| | | | Количество учеников | | |||
| СОР 1 | | | | | | | |
| СОР 2 | | | | | | | |
| СОЧ | | | | | | | |
| | Достигнутые цели | Цели, вызвавшие затруднения | |||||
| СОР 1 | | | |||||
| СОР 2 | | | |||||
| СОЧ | | | |||||