ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 324
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация |
| 1 | В | 1 | |
| 2 | В | 1 | |
| 3 | А | 1 | |
| 4 | В | 1 | |
| 5 | =5 – 4=1 | 1 | |
| = -1+3=2 | 1 | | |
| 6 | Поворот на угол 500 | 1 | |
| Поворот против часовой стрелки | 1 | | |
| Выполнение чертежа по условию задачи | 1 | | |
| 7 | Выполнен чертеж по условию задачи | 1 | |
| Использован коэффициент гомотетии | 1 | | |
| Построена гомотетичная фигура | 1 | | |
| 8 | Выполнен чертеж по условию задачи | 1 | |
| Применяется свойство биссектрисы АВ:ВС=АН:НС | 1 | Принимается альтернативная запись | |
| Вводится неизвестное, составлено и решено уравнение (28+х):х=43:29 Запись ответа: 58 и 86 | 1 | Принимается альтернативная запись | |
| 9 | Выполнен чертеж по условию задачи | 1 | |
| Доказано ∆ВОС⁓∆DОА (по двум углам) | 1 | | |
| 9:4=(х+25) : х | 1 | Принимается альтернативная запись | |
| х=20 | 1 | | |
| ВС=20см, АD=45см | 1 | | |
| Всего | 20 | | |
4 ВАРИАНТ
| Оценивание заданий работы | |||||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Количество баллов | 1 | 1 | 1 | 1 | 2 | 3 | 3 | 3 | 5 |
| Всего баллов | 20 баллов | ||||||||
-
Укажите координаты точки, симметричной точке В(-7; 3) относительно оси ординат
А) (-7; -3)
В) (7; 3)
С) (7; -3)
D) (-3; 7)
-
Какая фигура имеет центр симметрии и ось симметрии?
А) прямоугольный треугольник
В) параллелограмм
С) равнобокая трапеция
D) квадрат
-
Чтобы поворот имел место, должен быть задан:
А) угол поворота α
В) центр поворота О
С) центр поворота О и угол поворота α
D) фигура
-
Т очка О – центр правильного шестиугольника ABCDEFКМ. Укажите образ стороны АВ при повороте вокруг точки О по часовой стрелке на угол 900.
очка О – центр правильного шестиугольника ABCDEFКМ. Укажите образ стороны АВ при повороте вокруг точки О по часовой стрелке на угол 900.
А) АВ
В) DЕ
С) DС
D) МА
-
Параллельный перенос задан формулами =x – 6, = y+2 Найдите образ точки А(8; -1) при данном параллельном переносе. -
Построить треугольник А1В1С1, образованный поворотом вокруг точки В на 700 равнобедренного прямоугольного (с прямым углом В) треугольника АВС против часовой стрелки. -
Постройте треугольник К1L1М1 гомотетичный треугольнику КLМ с коэффициентом гомотетии равным 2. Центр гомотетии – точка О. -
В треугольнике АВС разность сторон АВ и ВС равна 18 см, а биссектриса ВН угла между ними делит третью сторону на отрезки 28 см и 12 см. Найдите стороны АВ и ВС -
В трапеции АВСD диагонали пересекаются в точке О. Точка пересечения диагоналей трапеции делит диагональ АС на отрезки 8см и 4см. Найдите основания трапеции АD и ВС, если их разность равна 25см. Выполните чертеж по условию задачи
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация |
| 1 | В | 1 | |
| 2 | D | 1 | |
| 3 | В | 1 | |
| 4 | С | 1 | |
| 5 | =8 – 6=2 | 1 | |
| = -1+2=1 | 1 | | |
| 6 | Поворот на угол 700 | 1 | |
| Поворот против часовой стрелки | 1 | | |
| Выполнение чертежа по условию задачи | 1 | | |
| 7 | Выполнен чертеж по условию задачи | 1 | |
| Использован коэффициент гомотетии | 1 | | |
| Построена гомотетичная фигура | 1 | | |
| 8 | Выполнен чертеж по условию задачи | 1 | |
| Применяется свойство биссектрисы АВ:ВС=АН:НС | 1 | Принимается альтернативная запись | |
| Вводится неизвестное, составлено и решено уравнение (18+х):х=28:12 Запись ответа: 13,5 см и 31,5 см | 1 | Принимается альтернативная запись | |
| 9 | Выполнен чертеж по условию задачи | 1 | |
| Доказано ∆ВОС⁓∆DОА (по двум углам) | 1 | | |
| 8:4=(х+25) : х | 1 | Принимается альтернативная запись | |
| х=25 | 1 | | |
| ВС=20см, АD=50см | 1 | | |
| Всего | 20 | | |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающих вопросы с множественным выбором ответов,с кратким и развернутым ответами.
В вопросах с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.
В вопросах, требующих краткого ответа, обучащийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/ вопросов
 Характеристика заданий суммативного оценивания за 3 четверть
Характеристика заданий суммативного оценивания за 3 четверть| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задания* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Решение треугольников | 9.1.3.8 Знать и применять формулы площади вписанного треугольника (S = abc , где a, b, c- 4R стороны треугольника, R-радиус описанной окружности), площади описанного многоугольника (S = p ∙ r, где r – радиус вписанной окружности, p - полупериметр многоугольника) | Применение | 1 | 1 | КО | 3 | 2 | 20 |
| 9.1.3.7 Знать и применять теорему синусов | Применение | 1 | 3 | КО | 4 | 2 | ||
| 9.1.3.6 Знать и применять теорему косинусов | Применение | 1 | 2 | КО | 6 | 3 | ||
| 9.1.3.9 Знать и применять формулы для нахождения радиуса окружности, используя площади вписанных и описанных треугольников | Применение | 1 | 4 | РО | 7 | 6 | ||
| 9.1.3.10 применять теоремы синусов и косинусов для решения треугольников и прикладных задач | Навыки высокого порядка | 2 | 5 | РО | 10 | 3 | ||
| 6 | РО | 10 | 4 | |||||
| ИТОГО: | | | 6 | | | 40 | 20 | 20 |
| Примечание: * - разделы, в которые можно вносить изменения | ||||||||
1 ВАРИАНТ
| Оценивание заданий работы | ||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество баллов | 2 | 3 | 2 | 6 | 3 | 4 |
| Всего баллов | 20 баллов | |||||
1. Радиус окружности, вписанной в треугольник, равен 12, а периметр треугольника равен 56. Найдите площадь треугольника.
2. Не вычисляя углов треугольника, определите его вид (по величине углов), если стороны треугольника равны:
а) 3; 5 и 6; b) 4; 5и 6; с) 3; 4 и 5.
3. В треугольнике АВС известно, что АВ = 14 см, ВС = 10 см, sin A = 0,2. Найдите синус угла Стреугольника.
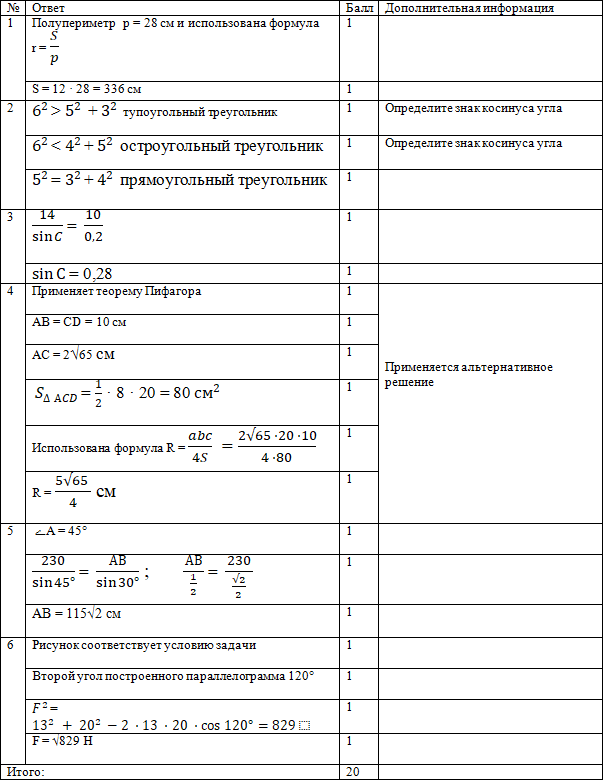
4. Основания равнобокой трапеции ABCD равны 8 см и 20 см, а высота – 8 см. Найдите:
-
диагональ трапеции АС; -
радиус окружности, описанной около трапеции.
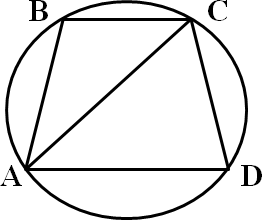
5. Определите ширину реки AB для геодезических измерений как показано на рисунке:
В 1050 ,
С 300 ,
ВС 230 м.
6. К одной точке приложили две силы: F1 = 13 H и F2 = 20 H под углом 60°. Найдите равнодействующую этих двух сил. Выполните рисунок.
Схема выставления баллов
1 вариант