ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 237
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
динамическое подобие в общем виде обуславливается равенством чисел:
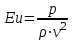 ;
;
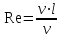 ;
;
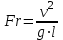 ;
;
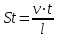 ,
,
где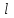 - характерный линейный размер;
- характерный линейный размер;
 - кинематическая вязкость жидкости;
- кинематическая вязкость жидкости;
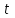 - время.
- время.
Все эти критерии являются определяющими лишь тогда, когда они выражены через исходные величины, задаваемые в начальных и граничных условиях.
1.12.а. ФОРМУЛЫ ПЕРЕСЧЕТА ХАРАКТЕРИСТИК ЦЕНТРОБЕЖНЫХ НАСОСОВ
Принимаем, что рассматриваем два однотипных центробежных насоса с геометрически подобными друг другу рабочими колесами, для которых известны соответствующие геометрические и энергетические параметры:
-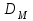 и
и 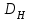 ;
;
-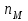 и
и 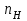 ;
;
-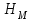 и
и 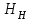 ;
;
-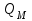 и
и 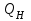 .
.
Из основного уравнения центробежного насоса для условий безударного входа имеем, что при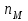 и
и 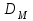 напор насоса равен:
напор насоса равен:
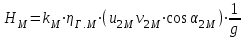 .
.
Соответственно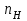 и
и 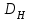 имеем:
имеем:
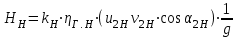 .
.
Отношение этих напоров равно:
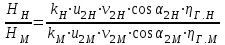 .
.
Исходя из условий геометрического подобия, можно считать, что:
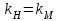
.
Исходя из условий кинематического подобия (подобия параллелограммов скоростей), можно считать, что:
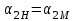
Отношение скоростей и
и 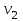 , согласно математическому выражению условий кинематического подобия, пропорционально отношению произведений
, согласно математическому выражению условий кинематического подобия, пропорционально отношению произведений 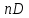 .
.
Следовательно, если подобные друг другу рабочие колеса насосов будут вращаться с различной частотой, то для создаваемых ими напоров можно написать соотношение:
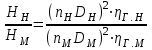 . (12.1)
. (12.1)
Подача насоса изменяется пропорционально изменению площади выходного сечения рабочего колеса и радиальной составляющей абсолютной скорости на выходе, тогда:
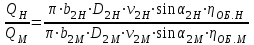 .
.
Поскольку рабочие колеса рассматриваемых насосов геометрически подобны, т. е.
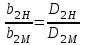 ,
,
то в общем случае с учетом условий кинематического подобия:
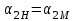 и
и
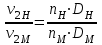
можно записать:
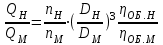 (12.2)
(12.2)
Мощность насоса изменяется пропорционально произведению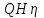 .
.
Подставляя вместо и
и 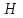 соответствующие величины из уравнений (12.1) и (12.2), имеем:
соответствующие величины из уравнений (12.1) и (12.2), имеем:
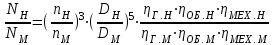 (12.3)
(12.3)
Уравнения (12.1 – 12.3), полученные на основе подобия лопастных насосов, называют формулами пересчета.
Эти формулы дают возможность с большой точностью рассчитывать основные параметры проектируемого насоса, если известны параметры насоса, геометрически ему подобного.
Эти формулы пересчета дают возможность после испытания насоса при одной частоте вращения определить его параметры для другой частоты.
Для пересчета гидравлического КПД насоса с модели на натуру наиболее оправдала себя полуэмпирическая формула А.А. Ломакина:
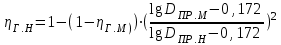
,
где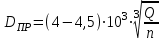 - приведенный диаметр входа в рабочее колесо, мм.
- приведенный диаметр входа в рабочее колесо, мм.
Объемные потери и механические потери в подшипниках и сальниках как немоделируемые должны подсчитываться по соответствующим формулам.
При малом отличии частоты вращения рабочих колес, а также их диаметров (для модели и натуры) формулы пересчета для предварительных расчетов можно представить в более удобном виде для решения практических задач:
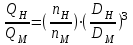 ;
;
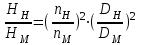 ;
;
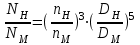 .
.
В том случае, когда один и тот же насос, перекачивающий одну и ту же жидкость, испытывается при различных частотах вращения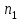 и
и 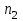 , формулы пересчета еще более упрощаются:
, формулы пересчета еще более упрощаются:
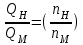 ;
;
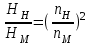 ;
;
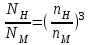 .
.
Одни и те же значения подачи и напора могут быть получены в насосах с различной частотой вращения. Естественно, что конструкция рабочих колес и всех элементов проточной части насоса, равно как и их размеры, при этом меняются.
Для сравнения лопастных насосов различных типов пользуются коэффициентом быстроходности, объединяя группы рабочих колес по принципу их геометрического и кинематического подобия.
Коэффициентом быстроходности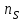 насоса называется частота вращения другого насоса, во всех деталях геометрически подобного рассматриваемому, но таких размеров, при которых, работая в том же режиме с напором 1 м, он дает подачу 0,075 м3/с.
насоса называется частота вращения другого насоса, во всех деталях геометрически подобного рассматриваемому, но таких размеров, при которых, работая в том же режиме с напором 1 м, он дает подачу 0,075 м3/с.
Численное значение коэффициента быстроходности можно определить, воспользовавшись формулами пересчета для однотипных насосов с рабочими колесами различных диаметров, работающих с переменной частотой вращения:
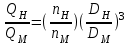 ;
;
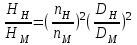 ;
;
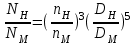
.
Применив эти формулы к данному насосу и геометрически подобному ему с рабочим колесом диаметром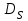 и частотой вращения
и частотой вращения  , получим:
, получим:
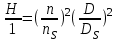 ;
;
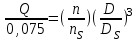 .
.
Исключив из этих выражений отношение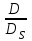 , найдем:
, найдем:
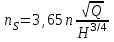 . (1*)
. (1*)
Для насосов двухстороннего входа вместо следует принимать
следует принимать 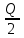 .
.
Подставив вместо подачи ее значение из формулы:
ее значение из формулы: 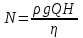
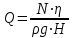
для насосов, перекачивающих воду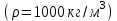 , получим другую формулу для определения коэффициента быстроходности:
, получим другую формулу для определения коэффициента быстроходности:
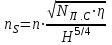 , (2*)
, (2*)
где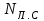 - мощность насоса в лошадиных силах.
- мощность насоса в лошадиных силах.
Значение коэффициента быстроходности изменяется в широком диапазоне:
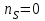 при
при 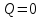 ;
;
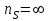 при
при 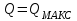 и
и 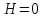 .
.
Для внесения определенности в понятие коэффициента быстроходности условились в формулы (1*) и (2*) подставлять оптимальные по КПД значения мощности, подачи и напора.
Из формулы (1*) вытекает, что:
Следовательно, тихоходные насосы (насосы с малым коэффициентом быстроходности) – это насосы, имеющие большой напор и сравнительно небольшую подачу.
Быстроходные насосы – насосы, имеющие меньший напор, но большую подачу.
Коэффициент быстроходности является очень важным удельным показателем, который широко используется в качестве характеристики типа насоса. Он одновременно учитывает три наиболее существенных параметра любого насоса:
Значение коэффициента быстроходности в известной степени определяет и форму рабочего колеса.
Для тихоходных центробежных насосов: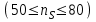
Поэтому тихоходные колеса имеют большие значения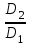 и малые значения
и малые значения 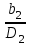 .
.
С увеличением быстроходности разница между выходным и входным диаметрами сокращается, а высота возрастает.
Коэффициент быстроходности пропорционален частоте вращения.
Повышение частоты вращения, как правило, ведет к уменьшению размеров и массы насоса и приводного двигателя.
Движение жидкости по всасывающему трубопроводу и подвод ее к рабочему колесу осуществляется за счет разности давления над свободной поверхностью жидкости в приемном резервуаре и абсолютного давления в потоке у входа в колесо.
Давление в области перед колесом не является постоянным. Оно определяется (зависит) от:
Для установления точной зависимости между всеми этими параметрами рассмотрим три возможных схемы установки центробежного насоса.
Схема 1. Забор насосом жидкости из открытого резервуара. Уровень свободной поверхности расположен ниже оси рабочего колеса насоса.
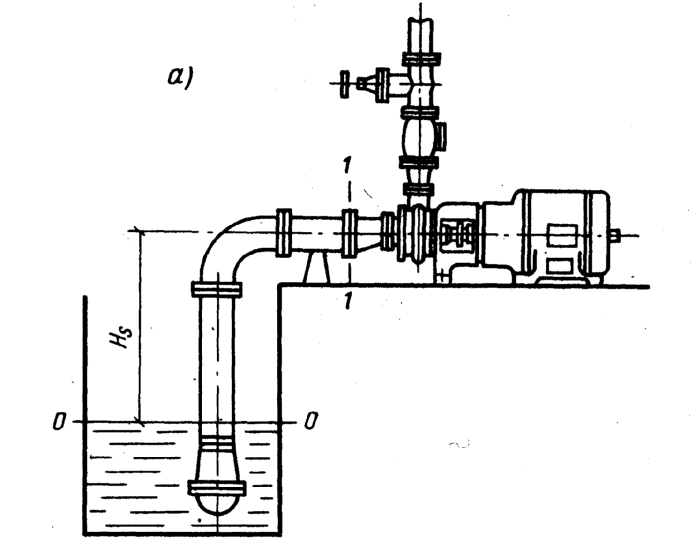
Применяя уравнение Бернулли для двух сечений (уровня свободной поверхности жидкости в приемном резервуаре О – О и сечения 1 – 1 на входе в насос) можно получить уравнение для определения абсолютного давления в сечении перед входом в насос:
-
Эйлера; -
Рейнольдса; -
Фруда; -
Струхаля.
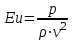 ;
;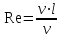 ;
;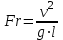 ;
;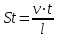 ,
,где
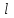 - характерный линейный размер;
- характерный линейный размер; - кинематическая вязкость жидкости;
- кинематическая вязкость жидкости;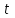 - время.
- время.Все эти критерии являются определяющими лишь тогда, когда они выражены через исходные величины, задаваемые в начальных и граничных условиях.
1.12.а. ФОРМУЛЫ ПЕРЕСЧЕТА ХАРАКТЕРИСТИК ЦЕНТРОБЕЖНЫХ НАСОСОВ
Принимаем, что рассматриваем два однотипных центробежных насоса с геометрически подобными друг другу рабочими колесами, для которых известны соответствующие геометрические и энергетические параметры:
-
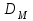 и
и 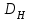 ;
;-
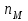 и
и 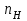 ;
;-
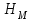 и
и 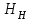 ;
;-
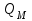 и
и 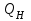 .
.Из основного уравнения центробежного насоса для условий безударного входа имеем, что при
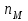 и
и 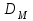 напор насоса равен:
напор насоса равен: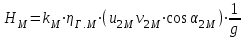 .
.Соответственно
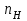 и
и 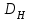 имеем:
имеем: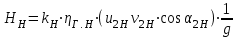 .
.Отношение этих напоров равно:
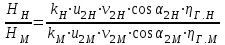 .
.Исходя из условий геометрического подобия, можно считать, что:
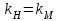
.
Исходя из условий кинематического подобия (подобия параллелограммов скоростей), можно считать, что:
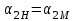
Отношение скоростей
 и
и 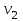 , согласно математическому выражению условий кинематического подобия, пропорционально отношению произведений
, согласно математическому выражению условий кинематического подобия, пропорционально отношению произведений 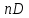 .
.Следовательно, если подобные друг другу рабочие колеса насосов будут вращаться с различной частотой, то для создаваемых ими напоров можно написать соотношение:
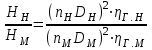 . (12.1)
. (12.1)Подача насоса изменяется пропорционально изменению площади выходного сечения рабочего колеса и радиальной составляющей абсолютной скорости на выходе, тогда:
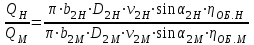 .
.Поскольку рабочие колеса рассматриваемых насосов геометрически подобны, т. е.
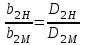 ,
,то в общем случае с учетом условий кинематического подобия:
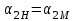 и
и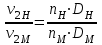
можно записать:
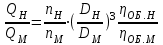 (12.2)
(12.2)Мощность насоса изменяется пропорционально произведению
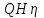 .
. Подставляя вместо
 и
и 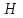 соответствующие величины из уравнений (12.1) и (12.2), имеем:
соответствующие величины из уравнений (12.1) и (12.2), имеем: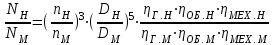 (12.3)
(12.3)Уравнения (12.1 – 12.3), полученные на основе подобия лопастных насосов, называют формулами пересчета.
Эти формулы дают возможность с большой точностью рассчитывать основные параметры проектируемого насоса, если известны параметры насоса, геометрически ему подобного.
Эти формулы пересчета дают возможность после испытания насоса при одной частоте вращения определить его параметры для другой частоты.
Для пересчета гидравлического КПД насоса с модели на натуру наиболее оправдала себя полуэмпирическая формула А.А. Ломакина:
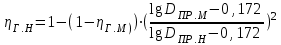
,
где
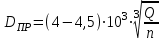 - приведенный диаметр входа в рабочее колесо, мм.
- приведенный диаметр входа в рабочее колесо, мм.Объемные потери и механические потери в подшипниках и сальниках как немоделируемые должны подсчитываться по соответствующим формулам.
При малом отличии частоты вращения рабочих колес, а также их диаметров (для модели и натуры) формулы пересчета для предварительных расчетов можно представить в более удобном виде для решения практических задач:
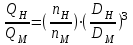 ;
;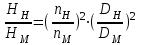 ;
;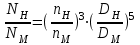 .
.В том случае, когда один и тот же насос, перекачивающий одну и ту же жидкость, испытывается при различных частотах вращения
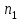 и
и 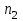 , формулы пересчета еще более упрощаются:
, формулы пересчета еще более упрощаются: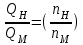 ;
;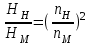 ;
;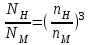 .
.-
КОЭФФИЦИЕНТ БЫСТРОХОДНОСТИ НАСОСА
Одни и те же значения подачи и напора могут быть получены в насосах с различной частотой вращения. Естественно, что конструкция рабочих колес и всех элементов проточной части насоса, равно как и их размеры, при этом меняются.
Для сравнения лопастных насосов различных типов пользуются коэффициентом быстроходности, объединяя группы рабочих колес по принципу их геометрического и кинематического подобия.
Коэффициентом быстроходности
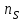 насоса называется частота вращения другого насоса, во всех деталях геометрически подобного рассматриваемому, но таких размеров, при которых, работая в том же режиме с напором 1 м, он дает подачу 0,075 м3/с.
насоса называется частота вращения другого насоса, во всех деталях геометрически подобного рассматриваемому, но таких размеров, при которых, работая в том же режиме с напором 1 м, он дает подачу 0,075 м3/с.Численное значение коэффициента быстроходности можно определить, воспользовавшись формулами пересчета для однотипных насосов с рабочими колесами различных диаметров, работающих с переменной частотой вращения:
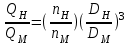 ;
;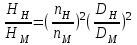 ;
;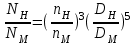
.
Применив эти формулы к данному насосу и геометрически подобному ему с рабочим колесом диаметром
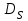 и частотой вращения
и частотой вращения  , получим:
, получим: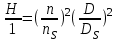 ;
;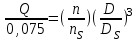 .
.Исключив из этих выражений отношение
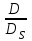 , найдем:
, найдем: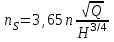 . (1*)
. (1*)Для насосов двухстороннего входа вместо
 следует принимать
следует принимать 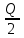 .
.Подставив вместо подачи
 ее значение из формулы:
ее значение из формулы: 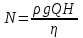
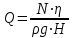
для насосов, перекачивающих воду
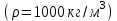 , получим другую формулу для определения коэффициента быстроходности:
, получим другую формулу для определения коэффициента быстроходности: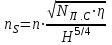 , (2*)
, (2*)где
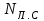 - мощность насоса в лошадиных силах.
- мощность насоса в лошадиных силах.Значение коэффициента быстроходности изменяется в широком диапазоне:
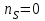 при
при 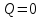 ;
;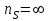 при
при 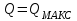 и
и 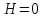 .
.Для внесения определенности в понятие коэффициента быстроходности условились в формулы (1*) и (2*) подставлять оптимальные по КПД значения мощности, подачи и напора.
Из формулы (1*) вытекает, что:
-
с увеличением напора коэффициент быстроходности насоса уменьшается; -
увеличение подачи приводит при прочих равных условиях к повышению коэффициента быстроходности.
Следовательно, тихоходные насосы (насосы с малым коэффициентом быстроходности) – это насосы, имеющие большой напор и сравнительно небольшую подачу.
Быстроходные насосы – насосы, имеющие меньший напор, но большую подачу.
Коэффициент быстроходности является очень важным удельным показателем, который широко используется в качестве характеристики типа насоса. Он одновременно учитывает три наиболее существенных параметра любого насоса:
-
частоту вращения; -
мощность (или подачу); -
напор.
Значение коэффициента быстроходности в известной степени определяет и форму рабочего колеса.
Для тихоходных центробежных насосов:
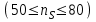
-
большой напор создается за счет увеличения диаметра рабочего колеса на выходе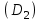 ;
; -
небольшая подача обуславливается малой высотой рабочего колеса у выхода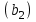 и малым его диаметром на входе
и малым его диаметром на входе 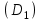 .
.
Поэтому тихоходные колеса имеют большие значения
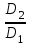 и малые значения
и малые значения 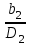 .
.С увеличением быстроходности разница между выходным и входным диаметрами сокращается, а высота возрастает.
Коэффициент быстроходности пропорционален частоте вращения.
Повышение частоты вращения, как правило, ведет к уменьшению размеров и массы насоса и приводного двигателя.
-
ВЫСОТА ВСАСЫВАНИЯ НАСОСОВ
Движение жидкости по всасывающему трубопроводу и подвод ее к рабочему колесу осуществляется за счет разности давления над свободной поверхностью жидкости в приемном резервуаре и абсолютного давления в потоке у входа в колесо.
Давление в области перед колесом не является постоянным. Оно определяется (зависит) от:
-
расположения насоса по отношению к уровню свободной поверхности приемного резервуара; -
гидравлического сопротивления на участке всасывающего трубопровода; -
скорости движения жидкости.
Для установления точной зависимости между всеми этими параметрами рассмотрим три возможных схемы установки центробежного насоса.
Схема 1. Забор насосом жидкости из открытого резервуара. Уровень свободной поверхности расположен ниже оси рабочего колеса насоса.

Применяя уравнение Бернулли для двух сечений (уровня свободной поверхности жидкости в приемном резервуаре О – О и сечения 1 – 1 на входе в насос) можно получить уравнение для определения абсолютного давления в сечении перед входом в насос: