Файл: Назначение и принцип действтия насосов.docx

.

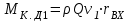Момент количества движения в сечении на выходе из межлопастного пространство рабочего колеса относительно оси насоса равен:

.

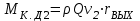Изменение момента количества движения массы жидкости за 1 секунду относительно оси рабочего колеса равно:

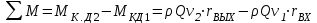. (1*)

Параллелограммы скоростей потока на входе в рабочее колесо центробежного насоса и на выходе из него показаны на рисунке:



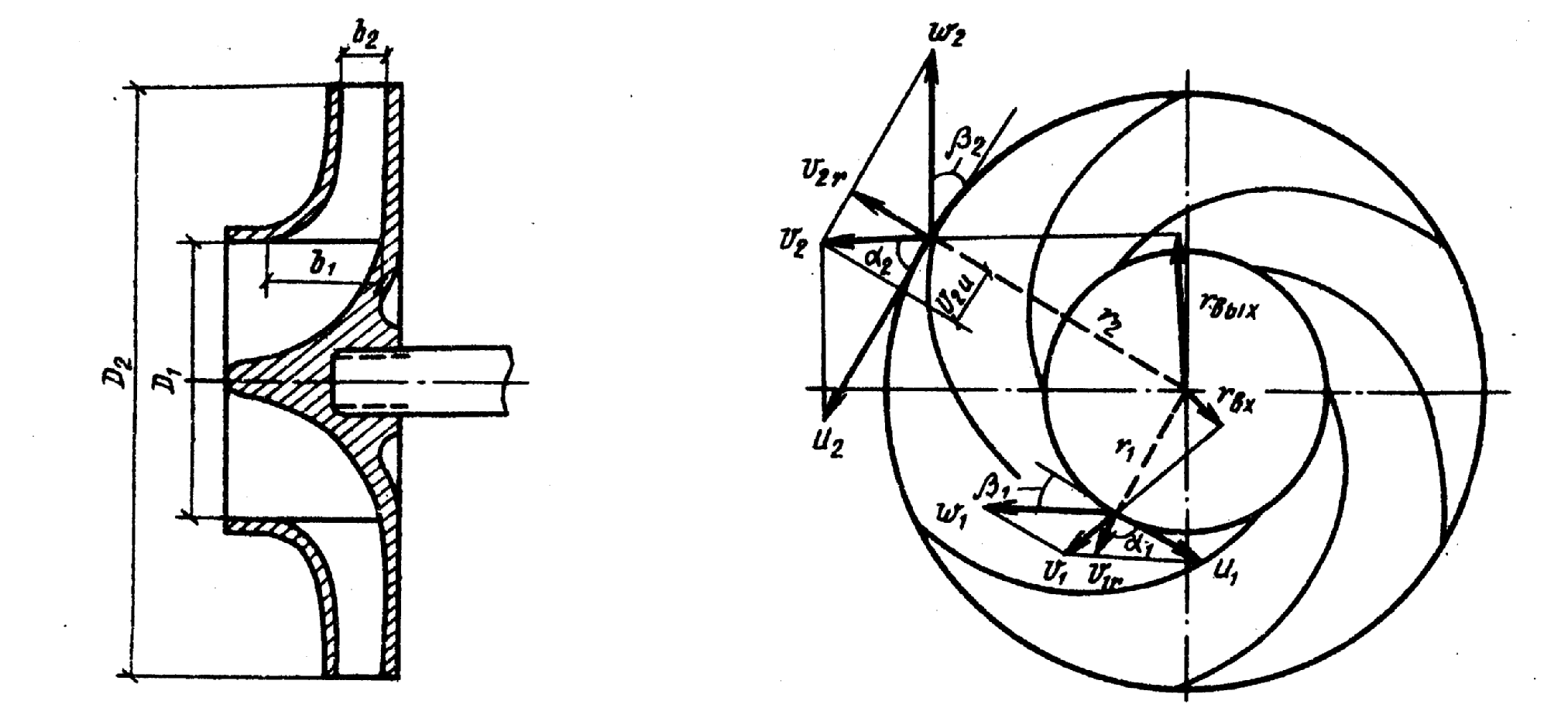
Из треугольника скоростей следует:

;

.

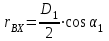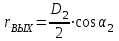В результате подстановки найденных значений для 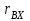и 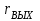в уравнение (*), имеем:

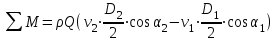. (2*)

Все внешние силы, действующие на массу жидкости, заполняющей межлопастные каналы рабочего колеса можно разделить на три группы:

• 
  Сила (силы) тяжести. Ее момент относительно оси вращения всегда равен нулю, так как рассматриваемый объем представляет собой тело вращения и его центр тяжести находится на оси колеса.
  
• 
  Давление на поверхностях контрольных сечений. Создаваемые этим давлением силы, проходят через ось вращения, и, следовательно, их момент также равен нулю,
  
• 
  Силы на обтекаемых поверхностях рабочего колеса. Главным образом, это:
  
  • 
    воздействие на протекающую жидкость сил давления со стороны лопастей рабочего колеса;
    
  • 
    силы трения жидкости на обтекаемых поверхностях.
    

Однако, последние силы малы и их моментом можно пренебречь.

Таким образом, момент всех внешних сил относительно оси вращения сводится к моменту динамического воздействия рабочего колеса 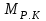на протекающую через него жидкость, т. е.

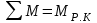. (3*)

В то же время известно, что мощность, передаваемая жидкости рабочим колесом насоса, равна произведению:

---

.

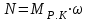
С другой стороны, та же мощность определяется подачей и напором:

.

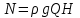Следовательно всегда должно соблюдаться равенство:

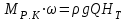, (4*)

где Н_Т – напор, создаваемый рабочим колесом насоса.

Поскольку последнее равенство написано без учета каких-либо потерь энергии, то напор Н_Т , называют также теоретическим.

Преобразуя уравнение (2*) с учетом выражений (3*) и (4*), получаем:

.

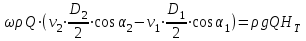Так как 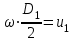и 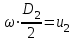, что вытекает из: 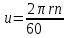, разделив обе части на 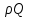, окончательно получаем:

.

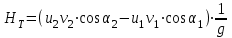Данная зависимость называется основным уравнением центробежного насоса.

Анализ основного уравнения позволяет установить, что напор центробежного насоса тем больше, чем больше переносная скорость 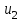на выходе из рабочего колеса.

Возможности повышения напора за счет:

• 
  увеличения выходного диаметра рабочего колеса ;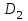
  
• 
  увеличения частоты вращения рабочего колеса ;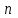
  
• 
  уменьшения угла .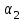
  

Теоретически произведение 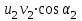имеет максимум при 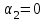, но что практически означает прекращение подачи.

При конструировании рабочих колес центробежных насосов обычно принимают .

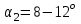При неизменных параметрах потока на выходе из рабочего колеса напор насоса, согласно основному уравнению, достигает максимума при условии:

,

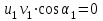что практически означает 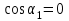или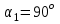

---

.

Из параллелограмма скоростей видно, что вектор абсолютной скорости жидкости 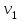должен быть направлен по радиусу, поэтому это условие называется условием радиального входа.

Условие радиального входа означает, что жидкость подводится к рабочему колесу без предварительного закручивания. Основное уравнение лопастного колеса центробежного насоса (уравнение Эйлера) принимает вид:

1. 
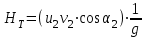
   11 а. ВЛИЯНИЕ ДДЕЙСТВИТЕЛЬНОГО ХАРАКТЕРА ДВИЖЕНИЯ ЖИДКОСТИ В РАБОЧЕМ КОЛЕСЕ НА ЗНАЧЕНИЕ ТЕОРЕТИЧЕСКОГО НАПОРА
   

В предыдущих параграфах были рассмотрены идеализированные схемы движения жидкости в межлопастных каналах рабочих колес центробежных насосов. Это позволило получить важную зависимость для определения теоретического напора в функции от кинематических параметров потока.

Однако на практике напор, развиваемый насосом, значительно меньше теоретического, что объясняется главным образом отличием действительной формы движения реальной жидкости от плоской картины потенциального течения.

Предположение о бесконечно большом числе бесконечно тонких лопастей в применении к рабочему колесу центробежного насоса означает, что поток в межлопастных каналах является осесимметричным и относительная скорость, которая определяется уравнением неразрывности для каждой точки рассматриваемого цилиндрического сечения, оказывается направленной по касательной к поверхности лопасти.

Действительное распределение относительных скоростей в каналах рабочего колеса конечных размеров не может быть осесимметричным из-за наличия силового взаимодействия между лопастью и потоком.

Для передачи энергии жидкости необходимо, чтобы давление на рабочих (выпуклых) поверхностях лопастей было больше, чем на тыльных, а это возможно лишь в том случае, если относительные скорости с рабочей стороны лопастей меньше, чем с тыльных.

Таким образом, при конечном числе лопастей рабочего колеса не все частицы жидкости получают одинаковое приращение энергии.

Вызванное этим обстоятельством понижение напора учитывается введением поправочного коэффициента 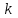к значению абсолютной скорости на выходе из колеса.

Обычно при числе лопастей рабочего колеса

---

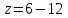
величина поправочного коэффициента изменяется от 0,75 до 0,90.

Другой причиной уменьшения напора по сравнению с его значением, подсчитанным по уравнению Эйлера, являются гидравлические потери.

Уменьшение теоретического напора вследствие гидравлических потерь оценивается введением в расчет гидравлического КПД, который в каждом конкретном случае может быть определен лишь экспериментальным путем.

С учетом действительного характера течения реальной жидкости в рабочем колесе насоса основное уравнение принимает вид:

,

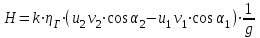где Н - напор насоса при конечном числе лопастей рабочего колеса;

- поправочный коэффициент, учитывающий, что при конечном числе лопастей рабочего колеса не все частицы жидкости получают одинаковое приращение энергии;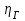

- гидравлический КПД, учитывающий гидравлические потери при движении жидкости.

1.12. ПОДОБИЕ НАСОСОВ

При проектировании новых насосов используются:

• 
  расчетно-теоретические разработки конструкций их проточной части;
  
• 
  опытные данные испытаний в лабораторных и натурных условиях;
  
• 
  опытные данные, получаемые в процессе эксплуатации аналогичных насосов.
  

Распространение полученных результатов исследований рабочих режимов на моделях и распространение полученных результатов на натурные насосы возможно на основе теории о механическом подобии движения реальной жидкости.

Главное положение этой теории заключается в необходимости выполнения условий геометрического, кинематического и динамического подобия.

Геометрическое подобие в гидромеханике означает подобие всех поверхностей, ограничивающих и направляющих поток.

Два насоса могут быть названы подобными, если все линейные размеры одного из них (модель) в одинаковое число раз меньше или больше соответствующих размеров другого (натура).

Математически геометрическое подобие сравниваемых насосов определяется постоянством линейного коэффициента подобия:

,

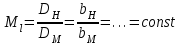где

---

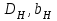
и 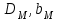- соответственно диаметр и высота рабочих колес натурного и модельного насосов.

Геометрическое подобие означает также постоянство отношений любых других размеров у модели и у натуры:

.

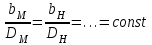Для полного соблюдения геометрического подобия необходимо подобие шероховатостей обтекаемых потоком поверхностей и зазоров между движущимися и неподвижными деталями насосов, т. е. необходимо , чтобы относительные шероховатости 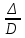и относительные зазоры 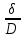были одинаковыми.

Кинематическое подобие в общем виде означает, что безразмерные поля скоростей в рассматриваемых потоках должны быть одинаковы, т. е. отношения скоростей всех соответствующих частиц жидкости, участвующих в движении, должны быть равны между собой, а траектории движения в сравниваемых гидравлических системах – геометрически подобны.

Применительно к насосам это, в частности означает подобие параллелограммов скоростей в соответствующих точках потока во всех элементах проточной части двух геометрически подобных машин, работающих в одинаковых режимах.

Математически условия кинематического подобия могут быть выражены в виде ряда отношений:

.

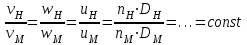Для соблюдения требований кинематического подобия необходимо также выдерживать постоянным отношение скорости протекания жидкости к скорости движения вращающихся деталей, т. е.

.

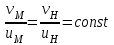Используя геометрическое подобие, из которого следует, что

1. ;

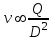2. ,

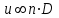получаем еще одно условие кинематического подобия, представляющее чрезвычайно большой практический интерес при моделировании насосов:

.

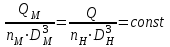Динамическое подобие кроме соблюдения условий геометрического и кинематического подобия означает пропорциональность сил, действующих в соответствующих точках потока.

При отнесении к этим силам сил:

• 
  давления;
  
• 
  вязкости;
  
• 
  тяжести;
  
• 
  инерции
  

---