Файл: Сені олынан брі келеді, тек зіе сен (кейбір сратарды жауабын таба алмадым, барымша істедім) жне матрицалары берілген.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 101
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
x=0 түзулерімен шектелген фигураның ауданы
+
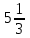
144. y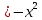
, 
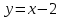y=0 түзулерімен шектелген фигураның ауданы
+
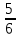
145. y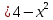
, 
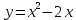түзулерімен шектелген фигураның ауданы
+9
146. y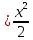
, 
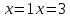түзулерімен шектелген фигураның ауданы
+
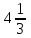
147. y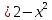
, 
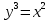түзулерімен шектелген фигураның ауданы
+
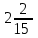
148. Меншіксіз интегралды есептеңіз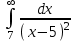
+0,5
149.
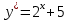дифференциалдық теңдеуінің шешімі:
+
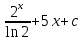
150.
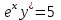дифференциалдық теңдеуінің шешімі:
+
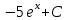151.xdy=5ydx дифференциялдық теңдеуінің дербес шешімін табыңыз, егер x=1 болғанда y=-1болса
+
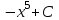152.
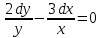, диф. теңдеуінің дербес шешімін табыңыз, егер х=1 болғанда 
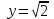болса
+
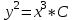
153. Берілген теңдеулердің арасынан айнымалылары ажыратылатын диф. теңдеуді көрсетіңіз:
*+
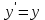
*+xy=(y+1)2
*+
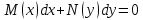
*+y=xeу
154. x=5, y=15 мәнiндегi xdy=ydx теңдеуiнiң шешiмiн табыңыз:
+у=3х
155.
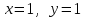
болғандағы,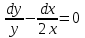
дербес шешiмiн табыңыз:
+
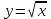
156. Айнымалылары ажыратылатын теңдеудi көрсетiңiз:
*+
*+xy=(y+1)2
*+
*+y=xeу
157.
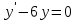дифференциалдық теңдеуiнiң шешiмi:
+
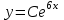
158.
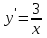дифференциалдық теңдеудiң шешiмi:
+3logx+C
159. Коши есебі: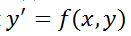
теңдеуінің барлық шешімдерінің арасынан у(х0)=у0, мұндағы х0,у0-берілген сандар,шартын қанағаттандыратын шешімін табу
керек. Мұндағы у0 саны:*+ізделінді функцияның бастапқы берілуі
160. Айнымалылары ажыратылған диф.теңдеу мына түрде жазылады:
Р(х,у)dх + G(x,y)dy = 0
161.
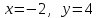болғандағы,
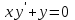дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз:
+
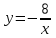
162.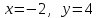 болғандағы, дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз:
+
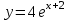
163.
163.Дифференциалдық теңдеу деп.....байланыстыратын қатынасты айтады
*+ х тәуелсіз айнымалыны, у(х) ізделінді функцияны және оның әртүрлі реттегі туындыларын
164. Ізделінді функция бір айнымалыдан тәуелді болса, онда дифференциалдық теңдеу.....деп аталады:: *+Қарапайым дифференциалдық теңдеу
165.Pdx+Qdy=0 түріндегі теңдеу, мұндағы P және Q - x және y тәуелді бірдей дәрежелі біртекті функциялар: бірінші ретті біртекті дифференциалдық теңдеу
166. Дифференциалдық теңдеудің реті: туындының жоғарғы ретін
167.Жалпы шешімнен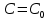
мәніне тең болғанда алынған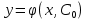 
функциясы
*+
дифференциалдық теңдеудің дербес шешімі
168. Коши есебі дегеніміз...
*+бастапқы шарттарды қанағаттандыратын дифференциалдық теңдеудің дербес шешімін табу
169. Айнымалылары ажыратылған дифференциалдық теңдеу
*+
170. Бiрiншi реттi сызықтық дифференциалдық теңдеу
+
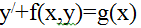
170.y’-6y=0 дифференциалдық теңдеуінің шешімі: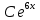
171.
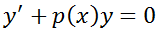теңдеуі
*+1-ші ретті біртекті сызықтық дифференциалдық теңдеу
172. 1-ші ретті біртекті сызықтық дифференциалдық теңдеудің жалпы fшешімі
*+
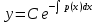
173. Дифференциалдық теңдеудің жалпы түрі
*+
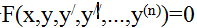
174. Бірінші ретті дифференциалдық теңдеудің жалпы шешімі
*+
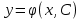
175. Толық дифференциалды M(x,y)dx+N(x,y)dy=0 теңдеуінің жалпы интегралы
*+
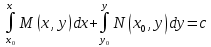
176. n-ші ретті дифференциалдық теңдеу
*+
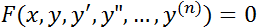
177. Дифференциалдық сызықтық біртекті теңдеудің түрі
+
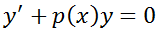
178. 1-ретті сызықтық біртекті емес дифференциалдық теңде
+
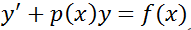
179.
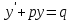түрiндегi теңдеу атауы, мұндағы p және q-функциялары x тәуелдi немесе тұрақты шамалар
*+1-ретті сызықты біртекті емес дифференциалдық теңдеу
179. Сызықтық біртекті емес дифференциалдық теңдеу:
*+
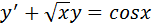
180. Сызықтық біртекті 1-ретті дифференциалдық теңдеудің жалпы шешімі
*+
181. Сызықтық біртекті емес 1-ретті дифференциалдық теңдеудің жалпы шешімі
*+
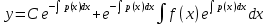
182. Сызықтық біртекті емес 1-ретті дифференциалдық теңдеудің шешудің әдісі: +Бернулли
183.
дифференциалдық теңдеудің шешудің әдісі
+Бернулли
184. Қай әдіспен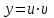
алмастыру арқылы сызықтық біртекті емес 1-ретті дифференциалдық теңдеудің шешімін іздейміз?
+Бернулли әдісімен
*+y=u(x)v(x)
185. Бернулли әдісінде
алмастыруда u функциясы
+белгісіз функция
186. Бернулли әдісінде алмастыруда v функциясы
+сәйкес біртекті теңдеудің дербес шешімі
187. дифференциалдық теңдеудің алмастыруда v функциясының шешімі
+
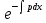
188. дифференциалдық теңдеудің алмастыруда u функциясының шешімі
+
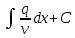
189. дифференциалдық теңдеудің Лагранж әдісінің басқа атауы
+тұрақтыларды варияциялау
190. дифференциалдық теңдеудің p, q ______ функциялар
+x-қа тәуелдi функциялар немесе тұрақты шамалар
+біртекті
191. Сызықтыбіртектідифференциалдықтеңдеу
*+
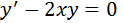
192. Сызықты біртекті емес дифференциалдық теңдеу
*+
+
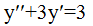
193. Сызықтық дифференциалдық теңдеу
+у'-2у/х=2х
194. Берілген дифференциалдық теңдеулердің қайсысы бірінші ретті сызықтық теңдеу болады
*+
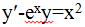
195. Бірінші ретті сызықтық дифференциалдық теңдеу:*+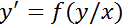
195. y-yctgx=2xsinx теңдеуді шешіңіз:*+y=(x2+С)sinx
196.
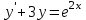теңдеуінің p(x), q(x)-?+ p(x)=3, q(x)= e2x
197. xdx+ydy=0 теңдеудi шешіңіз: -х
+
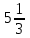
144. y
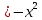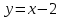, y=0 түзулерімен шектелген фигураның ауданы+
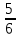
145. y
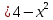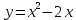, түзулерімен шектелген фигураның ауданы +9
146. y
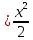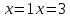, түзулерімен шектелген фигураның ауданы +
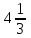
147. y
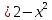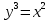, түзулерімен шектелген фигураның ауданы+
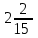
148. Меншіксіз интегралды есептеңіз
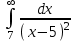
+0,5
149.
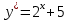дифференциалдық теңдеуінің шешімі:+
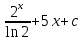
150.
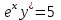дифференциалдық теңдеуінің шешімі: 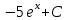+151.xdy=5ydx дифференциялдық теңдеуінің дербес шешімін табыңыз, егер x=1 болғанда y=-1болса
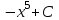+152.
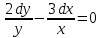, диф. теңдеуінің дербес шешімін табыңыз, егер х=1 болғанд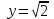а болса+
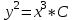
153. Берілген теңдеулердің арасынан айнымалылары ажыратылатын диф. теңдеуді көрсетіңіз:
*+
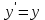
*+xy=(y+1)2
*+
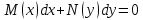
*+y=xeу
154. x=5, y=15 мәнiндегi xdy=ydx теңдеуiнiң шешiмiн табыңыз:
+у=3х
155.
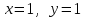
болғандағы,
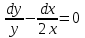дербес шешiмiн табыңыз:+
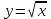
156. Айнымалылары ажыратылатын теңдеудi көрсетiңiз:
*+
*+xy=(y+1)2
*+
*+y=xeу
157.
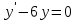дифференциалдық теңдеуiнiң шешiмi:+
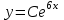
158.
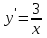дифференциалдық теңдеудiң шешiмi:+3logx+C
159. Коши есебі:
теңдеуінің барлық шешімдерінің арасынан у(х0)=у0, мұндағы х0,у0-берілген сандар,шартын қанағаттандыратын шешімін табу керек. Мұндағы у0 саны:*+ізделінді функцияның бастапқы берілуі
160. Айнымалылары ажыратылған диф.теңдеу мына түрде жазылады:
Р(х,у)dх + G(x,y)dy = 0
161.
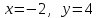болғандағы, 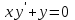дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз:+
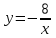
162.
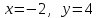болғандағы, дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз:+
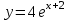
163.
163.Дифференциалдық теңдеу деп.....байланыстыратын қатынасты айтады
*+ х тәуелсіз айнымалыны, у(х) ізделінді функцияны және оның әртүрлі реттегі туындыларын
164. Ізделінді функция бір айнымалыдан тәуелді болса, онда дифференциалдық теңдеу.....деп аталады:: *+Қарапайым дифференциалдық теңдеу
165.Pdx+Qdy=0 түріндегі теңдеу, мұндағы P және Q - x және y тәуелді бірдей дәрежелі біртекті функциялар: бірінші ретті біртекті дифференциалдық теңдеу
166. Дифференциалдық теңдеудің реті: туындының жоғарғы ретін
167.Жалпы шешімнен
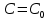мәніне тең болғанда алынған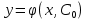
функциясы
*+
дифференциалдық теңдеудің дербес шешімі168. Коши есебі дегеніміз...
*+бастапқы шарттарды қанағаттандыратын дифференциалдық теңдеудің дербес шешімін табу
169. Айнымалылары ажыратылған дифференциалдық теңдеу
*+
170. Бiрiншi реттi сызықтық дифференциалдық теңдеу
+
170.y’-6y=0 дифференциалдық теңдеуінің шешімі:
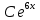
171.
теңдеуі *+1-ші ретті біртекті сызықтық дифференциалдық теңдеу
172. 1-ші ретті біртекті сызықтық дифференциалдық теңдеудің жалпы fшешімі
*+
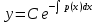
173. Дифференциалдық теңдеудің жалпы түрі
*+
174. Бірінші ретті дифференциалдық теңдеудің жалпы шешімі
*+
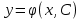
175. Толық дифференциалды M(x,y)dx+N(x,y)dy=0 теңдеуінің жалпы интегралы
*+
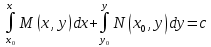
176. n-ші ретті дифференциалдық теңдеу
*+
177. Дифференциалдық сызықтық біртекті теңдеудің түрі
+
178. 1-ретті сызықтық біртекті емес дифференциалдық теңде
+
179.
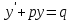түрiндегi теңдеу атауы, мұндағы p және q-функциялары x тәуелдi немесе тұрақты шамалар*+1-ретті сызықты біртекті емес дифференциалдық теңдеу
179. Сызықтық біртекті емес дифференциалдық теңдеу:
*+
180. Сызықтық біртекті 1-ретті дифференциалдық теңдеудің жалпы шешімі
*+
181. Сызықтық біртекті емес 1-ретті дифференциалдық теңдеудің жалпы шешімі
*+
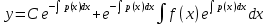
182. Сызықтық біртекті емес 1-ретті дифференциалдық теңдеудің шешудің әдісі: +Бернулли
183.
дифференциалдық теңдеудің шешудің әдісі+Бернулли
184. Қай әдіспен
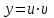алмастыру арқылы сызықтық біртекті емес 1-ретті дифференциалдық теңдеудің шешімін іздейміз?+Бернулли әдісімен
*+y=u(x)v(x)
185. Бернулли әдісінде
алмастыруда u функциясы+белгісіз функция
186. Бернулли әдісінде
алмастыруда v функциясы+сәйкес біртекті теңдеудің дербес шешімі
187.
дифференциалдық теңдеудің алмастыруда v функциясының шешімі+
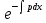
188.
дифференциалдық теңдеудің алмастыруда u функциясының шешімі+
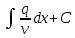
189.
дифференциалдық теңдеудің Лагранж әдісінің басқа атауы+тұрақтыларды варияциялау
190.
дифференциалдық теңдеудің p, q ______ функциялар+x-қа тәуелдi функциялар немесе тұрақты шамалар
+біртекті
191. Сызықтыбіртектідифференциалдықтеңдеу
*+
192. Сызықты біртекті емес дифференциалдық теңдеу
*+
+
193. Сызықтық дифференциалдық теңдеу
+у'-2у/х=2х
194. Берілген дифференциалдық теңдеулердің қайсысы бірінші ретті сызықтық теңдеу болады
*+
195. Бірінші ретті сызықтық дифференциалдық теңдеу:*+
195. y-yctgx=2xsinx теңдеуді шешіңіз:*+y=(x2+С)sinx
196.
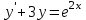теңдеуінің p(x), q(x)-?+ p(x)=3, q(x)= e2x197. xdx+ydy=0 теңдеудi шешіңіз: -х