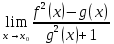Файл: Сені олынан брі келеді, тек зіе сен (кейбір сратарды жауабын таба алмадым, барымша істедім) жне матрицалары берілген.docx

Сделать презентацию

Скачать файл (2,15Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 392

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

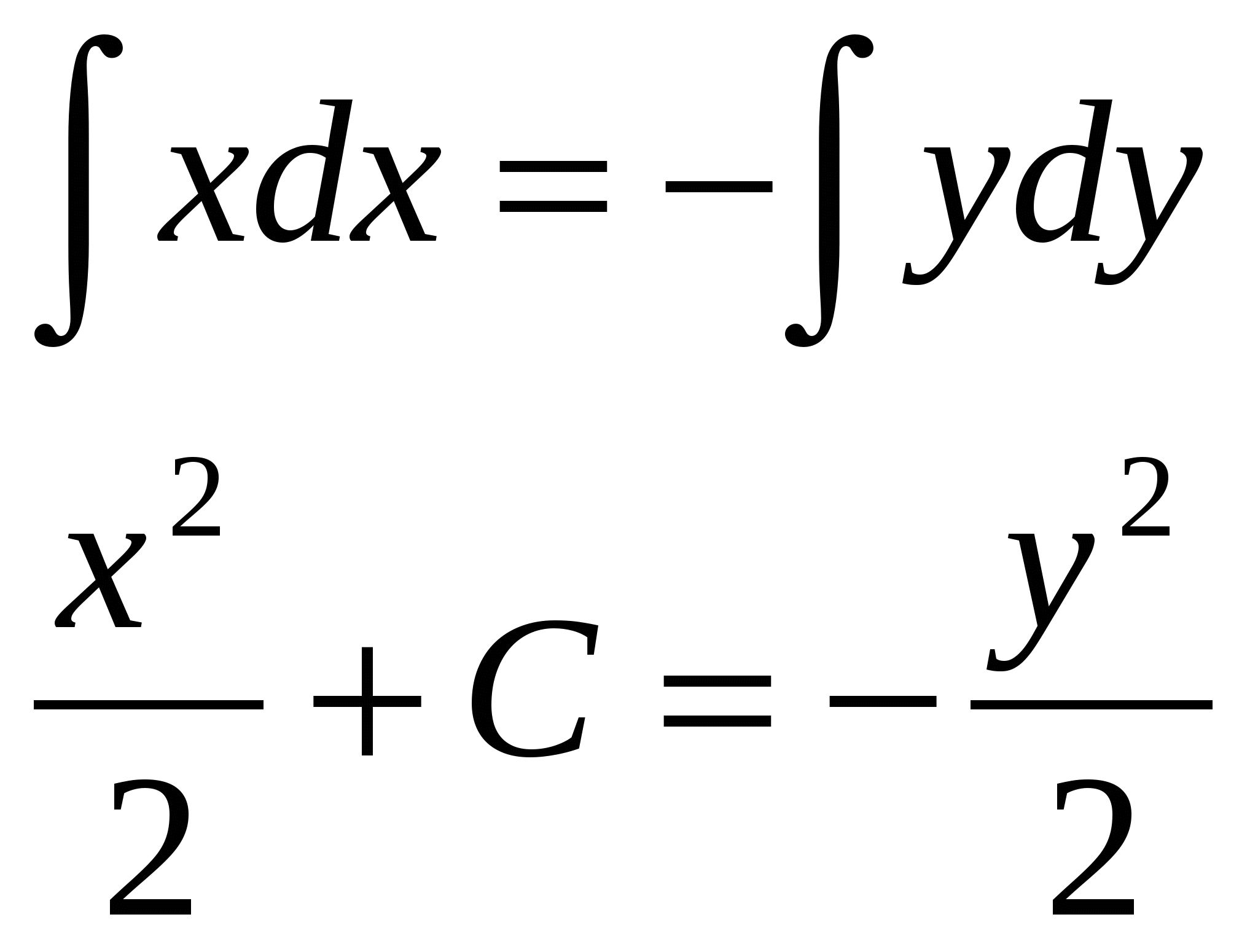
+ 198. 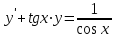теңдеудi шешіңіз+y=sinx+C*cosx199. 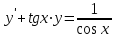теңдеуінің p(x), q(x)-?P(x)=tgx q(x)= 1/cosx200. 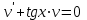теңдеудi шешіңіз+y=C*cosx201. у'-2у/х=х² теңдеудi шешіңіз+y= x^2(C+x) 202. у'-2у/х=2хтеңдеуінің p(x), q(x)-?+p(x)=-2/х,q(x)= 2х203. у'-2у/х=0 теңдеудi шешіңіз+y=х²C204. у'+у/х=хтеңдеуінің p(x), q(x)-?+ p(x)= 1/х, q(x)=x205. 2-ші ретті дифференциалдық теңдеу+ 206. 3-ші ретті дифференциалдық теңдеу*+ 207. 2-ші ретті дифференциалдық теңдеу*+ 208. дифференциалдық теңдеуінің реті: +4209. дифференциалдық теңдеуінің реті: +2210. дифференциалдық теңдеуінің реті: +3211. 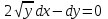дифференциалдық теңдеудің шешу әдісі: +айнымалыны алмастыру әдіс_{212. 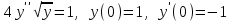Төменде көрсетілгендердің қайсысы «Коши есебі» болып табылады...}+ 213. 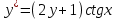дифференциалдық теңдеуді 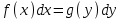түріне келтір+ctgx*dx=dy/2y+1214. 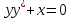дифференциалдық теңдеуді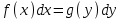

түріне келтір:-x*dx=ydy

215. 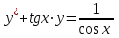сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек

p(x)=tgx g(x)=1/cosx

216. 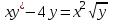сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек: p(x)=-4/х g(x)=х

217. 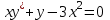сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек : p(x)=1/x g(x)=3x

218. Дифференциалдық теңдеудің жалпы шешімі 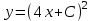және бастапқы шартты 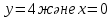белгілі болса, онда С неге тең

С=-2

219. Дифференциалдық теңдеудің жалпы шешімі 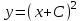және бастапқы шартты 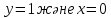белгілі болса, онда С неге тең: С=1

220. Дифференциалдық теңдеудің реті

*+туындының жоғарғы ретін

221. Дифференциалдық теңдеудің орнына қойғанда оны теңбе-теңдікке айналдыратын кез-келген функция...: *+дифференциалдық теңдеудің шешімі

222. Бірінші ретті дифференциалдық теңдеудің жалпы шешімі

*+

223. Коши есебі: теңдеуінің барлық шешімдерінің арасынан у(х₀)=у₀, мұндағы х₀,у₀-берілген сандар, шартын қанағаттандыратын шешімін табу керек. Мұндағы х₀ саны:

*+ тәуелсіз айнымалының бастапқы берілуі

224. мұндағы f(x) және g(y)-бір айнымалыдан тәуелді үздіксіз функциялар

*+айнымалылары ажыратылатын дифференциалдық теңдеу

225. 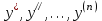теңдеуінің атауы, мұнда х – тәуелсіз айнымалы, у- ізделінді функция, - олардың туындылары: n-ші ретті дифференциалдық теңдеу

226. n-ші ретті дифференциалдық теңдеу: +

227. 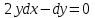дифференциалдық теңдеудің шешу әдісі +Айнымалыны ажырату_{228. Төменде көрсетілгендердің қайсысы «Коши есебі» болып табылады...}+y’+(x+1)y=x 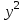, x(3)=1, y(0)=1229. 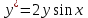дифференциалдық теңдеуді түріне келтір2sinx*dx=dy/y230. 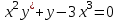сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек 231. Дифференциалдық теңдеудің жалпы шешімі және бастапқы шартты белгілі болса, онда С неге тең C=-2232. 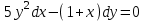дифференциалдық теңдеудің шешу әдісі+айнымалыны ажырату 233. 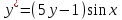дифференциалдық теңдеуді түріне келтірSinxdx=dy/5y-1234. 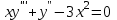дифференциалдық теңдеуінің реті+3235. xdy=ydx дифференциялдық теңдеуінің дербес шешімін табыңыз, егер x=1, y=4 болса Y=4x#32 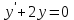дифференциалдық теңдеуінің шешімі:#33 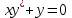дифференциалдық теңдеуінің шешімі:#34xdy=ydx дифференциялдық теңдеуінің дербес шешімін табыңыз, егер x=2, y=4 болса Ответ: 2_#35Решение уравнения 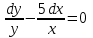, _{если х=1 ,}_y₌₁_{с= 1 , y(x)=cx^5}#37 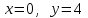болғандағы, дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз: Ответ: 4_{#38 Төменде көрсетілгендердің қайсысы «Коши есебі» болып табылады...}#39 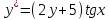дифференциалдық теңдеуді түріне келтір

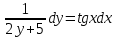
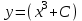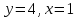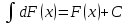
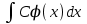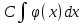
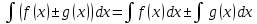
#40 Дифференциалдық теңдеудің жалпы шешімі және бастапқы шартты белгілі болса, онда С неге тең Ответ: 3#1 Алғашқы функцияның дифференциалынан алынған анықталмаған интеграл неге тең #2 Егер С – тұрақтысанболса, онда интегралы тең:#3*!Функцияның алгебралық қосындысының анықталмаған интегралы#4Егер F(x) функциясының туындысы f(x)-ке тең болса, онда F(x).....деп аталады: алғашқы функция#5 Анықталмаған интегралдың дифференциалы тең:интеграл таңбасының астындағы функцияға#6Егер F(x) функциясы f(x) үшін алғашкы функция болса, онда F(x)+c өрнегі ... 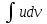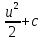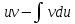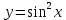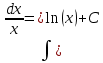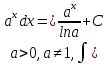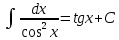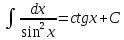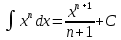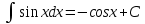деп аталады анықталмаған интеграл.#7 Функцияның анықталмаған интегралын есептеу процесi:интегралдау#8 =*= или_8.функциясының туындысы неге тең: sin2x#9#10 #11 #12#13 #14 #1*! 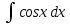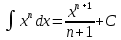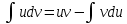интегралы үшін интегралдау әдісі:Тікелей интегралдау#2*!n-нiң қандай мәнiнде орындалмайды n=-1.#3*!Анықталмаған интеграл үшін бөліктеп интегралдау формуласы:#4*! 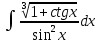интегралы үшін интегралдау әдісі Жаңа айн#5*!

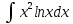
интегралындағы u=ln(x) және dv=x^2

#6*! 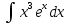интегралындағы u=x^3 және dv=e^x

#7*! интегралы үшін интегралдау әдісі Тікелей инт

#8*!Тікелей интегралдау әдісімен есептелетін интеграл

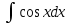
#9*! 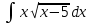интегралы үшін интегралдау әдісі Жаңа айн

#10*! интегралы үшін интегралдау әдісі Жаңа айн

#11*! 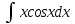интегралы үшін интегралдау әдісі: Бөліктеп интегралдау

#14*! 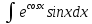алмастыру Жаңа айн

#1 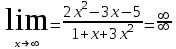_{Берілген анықталмағандықты ашу әдісі:}_{алымын да, бөлімін де х-тің ең үлкен дәрежесіне бөлу}

#2 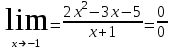_{. Берілген анықталмағандықты ашу әдісі:}_{көпмүшені көбейткіштерге жіктеу}

#3 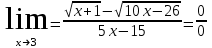_._{Берілген анықталмағандықты ашу әдісі:}_{Алымын және бөлімін түйіндес өрнекке көбейту}

#4 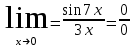_{. Берілген анықталмағандықты ашу әдісі:}_{Тамаша шекке келтіру}

#5 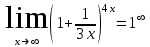_{. Берілген анықталмағандықты ашу әдісі:}_{Тамаша шекке келтіру}

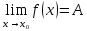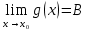#6 Егер және , онда 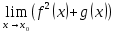шегі тең: *+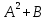
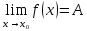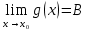#7 Егер және , онда 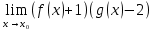шегі тең*+(А+1)(В-2)

#8Егер 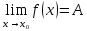және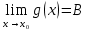 , онда