По содержанию все задачи делятся на абстрактные и конкретные. Абстрактные – это те задачи, в которых нет конкретных числовых значений, и которые решаются в общем виде. Абстрактная задача выявляет более глубоко физическую сущность явлений, не отвлекая учащихся на конкретные несущественные детали. Конкретные задачи легче для учащихся, потому что конкретные числа приближают задачу к уровню развития ребёнка, который не научился ещё абстрагировать.



Рис. 2. Классификация физических задач по содержанию.

По степени сложности задачи делятся на простые, сложные, задачи повышенной сложности (трудности) и творческие. Простые – с использованием одной формулы. Они носят тренировочный характер и решаются обычно сразу же на закрепление нового материала. Сложные – с использованием нескольких формул. Эти формулы могут быть из разных тем. Повышенной сложности – связывающие в одну проблему несколько разделов. (Часто бывает, что для учеников сложность вызывает не физическая, а математическая составляющая решения задачи).

Творческие – алгоритм решения которых ученику не известен. Это могут быть задачи, по классификации Разумовского, исследовательские или конструкторские. Исследовательская задача отвечает на вопрос «почему?», а конструкторская – на вопрос «как сделать?»

По основному способу выражения условия задачи делятся на текстовые, экспериментальные, графические и задачи-рисунки.

По способу решения задачи делятся на качественные, вычислительные, графические, экспериментальные.



Рис. 3. Классификация физических задач по способу решения.

Отличительная особенность качественных задач в том, что их условия акцентируют внимание учащихся на физической сущности рассматриваемых явлений. Решаются они, как правило, устно, путём логических умозаключений.

Вычислительные задачи – это задачи, которые могут быть решены только с помощью вычислений и математических действий.

Графические и экспериментальные задачи – это задачи, решаемые с помощью графика или с помощью эксперимента.

---

4. Как решается задача.

Для того, чтобы научить учеников решать задачи, необходимо представлять себе, какова структура мыслительной деятельности ученика по решению задачи.



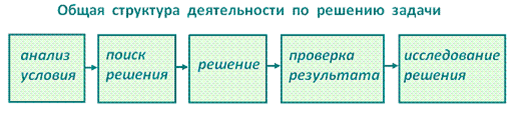
Рис. 4. Структура деятельности при решении задач на уроках физики.

Самый важный – первый момент – анализ условия. Ученик должен не только запомнить условие, но и осознать его. Иначе решение задачи превратится в «пойди туда, не знаю куда, и принеси то, не знаю что».

Проверить понимание задачи учитель может, попросив ученика повторить формулировку задачи, выделить главные элементы задачи: неизвестные и данные. При решении задачи учеником у доски должно стать правилом самостоятельное произнесение учеником формулировки задачи без использования учебника или подсказок.

На этапе поиска решения ученик вспоминает физические законы, определения, описывающие ту область явлений, о которой говорится в задаче и составляет план решения. Этот этап самый сложный, на него приходится большая доля мысленных усилий.

Существуют различные методы поиска решения задачи. Учащихся желательно ознакомить с ними, показывая, в каких случаях удобнее использовать тот или иной из них.

Основные методы поиска решения задачи: анализ и синтез. Но обычно в чистом виде они не используются, и самым распространённым является аналитико-синтетический способ.

При решении задач анализ может выступать в двух формах: а) когда в рассуждениях двигаются от искомых к данным задачи; б) когда целое расчленяют на части. Соответственно, синтез – это рассуждение: а) когда двигаются от данных задачи к искомым; б) когда элементы объединяют в целое.

Найденное известное решение задачи обычно излагают синтетическим методом, а чтобы найти способ решения, обычно пользуются анализом. Синтез позволяет изложить известное решение задачи быстро и чётко. Однако ученику при этом трудно понять, как было найдено решение, как бы он сам мог догадаться решить задачу. (Особенно это хорошо видно на примере доказательства некоторых особо сложных теорем математики.

Проводятся некоторые преобразования, искусственные приёмы с введением замен, подстановками и, в конце концов, теорема оказывается доказанной. А сам процесс нахождения доказательства остался «за кадром»). Анализ требует большей, чем синтез, затраты учебного времени, но зато позволяет показать ученику, как найти решение, как можно самому догадаться её решить. Если анализ используется систематически, то у учащихся формируются навыки поиска решения задач.

---

Анализ в чистом виде вообще не применяется. Если ученик пользуется им при поиске решения задачи, то только до тех пор, пока в его сознании не возникнет идея решения. При решении задачи синтезом в сознании человека проводится и анализ, но часто настолько быстро, подсознательно, что ему кажется, будто он сразу увидел решение, не прибегая к анализу.

На этапе решения идут преобразования записанных формул, осуществляется намеченный план решения.

Проверка результата – проверка, прикидка достоверности, полученного результата.

Исследование решения предполагает, что задача будет немного изменена, и ученик поисследует физическое явление. Этот очень важный этап часто опускается учителем, в то время, как его дидактические возможности огромны. Необходимо помнить, что никакую задачу нельзя исчерпать до конца, всегда остаётся что-то, над чем можно поразмышлять; изменив условие и решив полученную задачу, можно глубже проанализировать физическое явление; в ряде случаев можно найти другое решение этой же задачи.

Основные средства учителя, позволяющие научить решать задачи:

1) Образец решения задачи. Такой образец полезен на первом этапе, но его дидактическая ценность невелика.

2) Алгоритмическое предписание. По такому предписанию легко решаются задачи, например, в кинематике.

Но сложные творческие задачи не решаются по образцу или алгоритмическому предписанию. Для их решения учащиеся сами должны «изобрести» (составить) способ решения. А для этого:

• Они должны знать и владеть общими эвристическими методами их решения. Эти общие методы следует сообщать учащимся постепенно и регулярно, иллюстрируя достаточным числом примеров.

• Больше решать задач самостоятельно, т. к. любые умения и навыки приобретаются только в практике. При этом решение задач учениками должно быть мотивированным, т. к. эффективность поиска решения прямо зависит от стремления его найти.

Поэтому добавим ещё два средства:

3) Обучение эвристическим методам решения задач на большом числе примеров.

4) Самостоятельное и заинтересованное решение учащимися задач, способ решения которых им не известен, но материал которых не выходит за рамки их знаний.

Образец оформления любой задачи

---

Решение задач должно быть полностью расписано.

Оформление задач делается всегда простым карандашом и заполняется синей ручкой по стандартной форме:

Дано: (клеток 9)	SI (СИ): (клеток 7)	Решение: (клеток: до красной линии)
Найти:
Рис. 5. Стандартный образец оформления задачи. Ответ: !!! SI (СИ): если нет или не надо что-то переводить, то просто ставим – прочерк напротив данной величины. !!! Широко не пишите, как можно компактнее. Экономьте место.

Рефлексия.

1. Какие классификации задач по физике существуют? Опишите их.

2. Назовите основные средства учителя, позволяющие научить решать задачи по физике на разные темы.

3. Как решаются задачи по физике?
1.2. Различные приемы и способы решения физических задач: алгоритмы, аналогии, геометрические приемы, метод размерностей, графические решения
Цели: познакомить учащихся с классификациями задач и напомнить ребятам требования к оформлению любой рассчётной задачи по физике на уроках в школе или парах в профильных ВУЗах.

При решении физических задач могут быть использованы арифметический, алгебраический, графический, геометрический способы.

Далее рассмотрим подробнее каждый из способов.

Задача №1. Какой максимальной массы груз может выдержать в пресной воде плот, связанный из 25 сосновых бревен? Объем каждого бревна в среднем 0,8 м³.



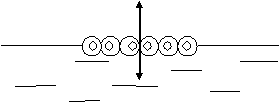
Рис. 6. Плот на воде.

Решение начинается с анализа условия, выполнения чертежа к задаче, записи условия. Изображают силы, действующие на плот, говорят о том, что грузоподъемность плота равна разности сил, действующих на плот.

Арифметический способ

---

предполагает следующее решение данной задачи:

Каков объем всех бревен плота?

пл=nV;

V_пл=0,8 м³*25=20 м³  

2.      Чему равна масса плота?

m_пл=ρV;

m_пл=500 кг/м³*20 м³=10 000 кг  

3.      Какова сила тяжести, действующая на плот?

Т=m_плg;

F_Т=9,8 Н/кг*10000 кг=98 000 Н

4.      Какова Архимедова сила, действующая на плот?

F_A=ρ_вgV_пл;

F_A=1000 кг/м³*9,8 Н/кг*20 м³=196 000 Н

5.      Каков вес груза, который может выдержать плот?

P=F_A – F_T;

P=196 000 Н-98 000 Н=98 000 Н  

6.      Какова масса груза?

m_гр=P/g;

m_гр=98 000 Н/ 9,8 Н/кг=1000 кг.
Посмотрим, как это задача решается алгебраическим способом. Анализируя задачу, записываем:

P= F_A - F_T.  

Знаем, что

F_A=ρ_вgV, V=nV₁ или F_A=ρ_вg nV₁;

Т=m_плg; m_пл=ρV=ρnV₁, то есть F_Т=ρ nV₁*g

Окончательно получим:

P= ρ_вnV₁g – ρg nV₁= g nV₁ (ρ_в - ρ) = 25*0,8м³* (1000кг/м³-500кг/м³)

Проиллюстрируем решение задачи геометрическим способом.

Задача №2. Посередине троса длиной 10 м подвесили фонарь массой 10 кг. Определить силу натяжения троса, если длина прогиба троса 0,5 м.



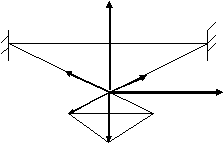
Рис. 7. Закреплённый трос с фонарём.
Записываем условие задачи, делаем чертеж. На фонарь действуют сила тяжести т=m и силы натяжения троса 1, 2, равные по модулю Т

---

Смотрите также файлы

• Страдательные причастия настоящего времени Повторение изученного.pptx

• 3 Криптографические методы защиты информации. (4 ак ч.) 3.docx

• Лекция использование цифровых технологий для индивидуализации обучения.docx

• Протокол 1 от августа 2022года Руководитель шмо О. С. Михайлюта Согласовано.docx

• Задание 1 Сформулируйте цели и задачи прохождения практики с учетом задач практики, установленных в программе практики, описав в отчете исходные данные, условия задачи и цели ее решения.docx