Файл: Протокол 3 от Председатель педагогического совета Габдулин Х. В. Согласовано.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 163
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1=Т2=Т. Фонарь находится в равновесии, значит, т+ 1+ 2 =0. Связываем с фонарём систему координат, обозначаем направления осей. Запишем условие равновесия фонаря в проекциях на оси: Т1xCos+Т2xCos=0; 2ТСos=0Tу+Т 1уSin+Т2уSin=0; - mg+2ТSin=0 Из треугольника ВОС находим: Sin=ОВ/ОС=2h/l (ОСВС) С учетом этого получают: - mg+2Т=0, откуда Т= 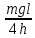 .
.
Задачу можно решить, пользуясь подобием треугольников ВОС и MON. Треугольник MON образован половиной силы тяжести, действующей на фонарь, и силой Р, действующей на трос (равной по модулю Т). Учитывая, что ON =Fт/2 (половина диагонали ромба), получают: 2h/l= Fт/2Т.
Откуда: Т=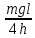
Решим следующую задачу графическим способом.
Задача №3. По графику опишите движение тела, определите время, проекцию перемещения и проекцию ускорения на отдельных участках движения тела.
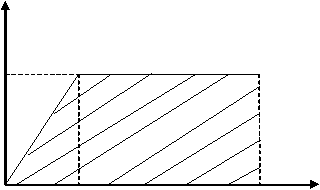
Рис. 8. График движения тела.
При анализе условия, устанавливают, что на графике приведена зависимость проекции скорости тела от времени. Начальная скорость =0 (при t=0). Вначале тело движется с ускорением, так как проекция его скорости возрастает от нуля до . Если график - прямая линия, значит движение равноускоренное и проекция его ускорения /t1, а проекция перемещения численно равна площади треугольника OAD. Проекция перемещения . Это формула проекции перемещения для данного вида движения. В промежуток времени проекция скорости не менялась, тело двигалось равномерно. Проекция перемещения за это время численно равно площади прямоугольника ABCD, а проекция перемещения за время - площади трапеции OABC.
Арифметический способ, предполагает решение задачи по действиям, по вопросам. Сначала записываем формулу, сразу же вычисляют содержащуюся в ней неизвестную величину. По сравнению с этим способом алгебраический более экономный, но он требует определенных знаний по математике. При решении геометрическим способом, школьники должны обладать знаниями в области геометрии. Объектом исследования в задачах решаемых графическим способом является график. В одних задачах нужно проанализировать график и условие в задаче задано графиком. В других задачах график необходимо построить по данным приведенным в задаче.
Рефлексия.
1.3. Примеры задач всех видов.
Цели: познакомить учащихся с классификациями задач и напомнить ребятам требования к оформлению любой рассчётной задачи по физике на уроках в школе или парах в профильных ВУЗах.
Примеры решения задач на ЗСЗ (закон сохранения заряда) и закон Кулона
1. Три капли имеющие заряды соответственно 2q, -3q, - q, слились в одну. Определите суммарный заряд большой капли.
2. Два одинаковых металлических шарика, имеющих заряды + 150 нКл и – 60 нКл, привели в соприкосновение и раздвинули на прежнее место. Каким станет их заряд?
3. С какой силой взаимодействуют два заряда по 10 нКл, находящиеся на расстоянии 3 см друг от друга?
4. На каком расстоянии друг от друга заряды 1 мкКл и 10 нКл взаимодействуют с силой 9 мН?
5. Во сколько раз надо изменить расстояние между зарядами при увеличении одного из них в 25 раз, чтобы сила взаимодействия осталась прежней?
6. Капля масла находится в однородном электрическом поле, на которую действует сила 56 нН. Напряженность электрического поля равна 400 Н/Кл. Определите заряд капли масла. Вычислите количество избыточных электронов в капле масла.
7. Чему равна напряженность поля, созданного зарядом +2 нКл в точке, удаленной от заряда на расстояние 10 см в воде?
8. Чему равен потенциал в точке эквипотенциального поля, созданного зарядом +2 нКл в точке, удаленной от заряда на расстояние 10 см в воде?
9. Две параллельные металлические пластины, расположенные на расстоянии 4 см. Потенциалы на верхних и нижних пластинах равны соответственно 2000 В и 800 В. Найдите напряженность однородного поля между пластинами. Чему равна работа по перемещению заряда, равного 20 мкКл. Вычислите электроемкость конденсатора.
10. От каких факторов зависит электроемкость конденсатора?
1) От площади и формы обкладок
2) От расстояния между обкладками и удельного сопротивления их вещества
3) От наличия между обкладками диэлектрика и его цвета
4) От площади обкладок, расстояния между ними и наличия диэлектрика (т.к. это следует из формулы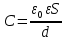 – электроемкость плоского конденсатора )
– электроемкость плоского конденсатора )
Примеры решения задач на второй закон Ньютона в 10 классе
Пример 1.
Какую силу нужно приложить, чтобы магнит массой 70 г, прилипший к стальной вертикальной плите, равномерно переместить вертикально вверх? Для равномерного движения магнита вертикально вниз прикладывают силу 2,5 Н.
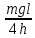 .
. Задачу можно решить, пользуясь подобием треугольников ВОС и MON. Треугольник MON образован половиной силы тяжести, действующей на фонарь, и силой Р, действующей на трос (равной по модулю Т). Учитывая, что ON =Fт/2 (половина диагонали ромба), получают: 2h/l= Fт/2Т.
Откуда: Т=
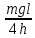
Решим следующую задачу графическим способом.
Задача №3. По графику опишите движение тела, определите время, проекцию перемещения и проекцию ускорения на отдельных участках движения тела.

Рис. 8. График движения тела.
При анализе условия, устанавливают, что на графике приведена зависимость проекции скорости тела от времени. Начальная скорость =0 (при t=0). Вначале тело движется с ускорением, так как проекция его скорости возрастает от нуля до . Если график - прямая линия, значит движение равноускоренное и проекция его ускорения /t1, а проекция перемещения численно равна площади треугольника OAD. Проекция перемещения . Это формула проекции перемещения для данного вида движения. В промежуток времени проекция скорости не менялась, тело двигалось равномерно. Проекция перемещения за это время численно равно площади прямоугольника ABCD, а проекция перемещения за время - площади трапеции OABC.
Арифметический способ, предполагает решение задачи по действиям, по вопросам. Сначала записываем формулу, сразу же вычисляют содержащуюся в ней неизвестную величину. По сравнению с этим способом алгебраический более экономный, но он требует определенных знаний по математике. При решении геометрическим способом, школьники должны обладать знаниями в области геометрии. Объектом исследования в задачах решаемых графическим способом является график. В одних задачах нужно проанализировать график и условие в задаче задано графиком. В других задачах график необходимо построить по данным приведенным в задаче.
Рефлексия.
-
Сколько всего существует основных способов решения задач по физике? И какие это способы? -
Опишите каждый способ решения задач на уроках физики?
1.3. Примеры задач всех видов.
Цели: познакомить учащихся с классификациями задач и напомнить ребятам требования к оформлению любой рассчётной задачи по физике на уроках в школе или парах в профильных ВУЗах.
Примеры решения задач на ЗСЗ (закон сохранения заряда) и закон Кулона
1. Три капли имеющие заряды соответственно 2q, -3q, - q, слились в одну. Определите суммарный заряд большой капли.
| Дано: q1 = 2q q2 =-3q q3 =-q | СИ: - - - | Решение: qобщ. = q1 + q2 + q3 qобщ = 2q -3q –q = -2q |
| Найти: qобщ. - ? | | Ответ: -2q |
2. Два одинаковых металлических шарика, имеющих заряды + 150 нКл и – 60 нКл, привели в соприкосновение и раздвинули на прежнее место. Каким станет их заряд?
| Дано: q1 = +150 нКл q2 =-60 нКл | СИ: - - - | Решение: Если два тела, обладающие зарядами, привели в соприкосновение, то их заряд станет одинаковым, из закона сохранения заряда вытекает... 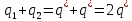 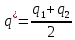 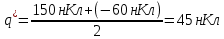 |
| Найти: q/ - ? | | Ответ: 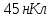 |
3. С какой силой взаимодействуют два заряда по 10 нКл, находящиеся на расстоянии 3 см друг от друга?
| Дано: q1 = 10 нКл q2 = 10 нКл r = 3 см ε = 1 | СИ: 10*10-9 Кл 10*10-9 Кл 3*10-2 м | Решение: 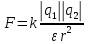 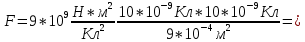 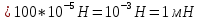 |
| Найти: F - ? | | Ответ: 1 мН |
4. На каком расстоянии друг от друга заряды 1 мкКл и 10 нКл взаимодействуют с силой 9 мН?
| Дано: q1 = 1 мкКл q2 = 10 нКл F = 9 мН ε = 1 | СИ: 1*10-6 Кл 10*10-9 Кл 9*10-3 Н | Решение: 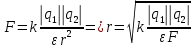 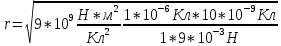 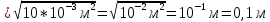 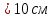 |
| Найти: r - ? | | Ответ: 10 см. |
5. Во сколько раз надо изменить расстояние между зарядами при увеличении одного из них в 25 раз, чтобы сила взаимодействия осталась прежней?
| Дано: q1 = q1 q2 25 q2 F1=F2=F ε = 1 | СИ: - - | Решение: F1=F2 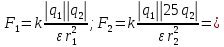 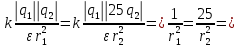 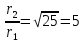 |
| Найти: 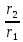 - ? - ? | | Ответ: увеличить в 5 раз. |
6. Капля масла находится в однородном электрическом поле, на которую действует сила 56 нН. Напряженность электрического поля равна 400 Н/Кл. Определите заряд капли масла. Вычислите количество избыточных электронов в капле масла.
| Дано: F = 56 нН E = 400 Н/Кл=4*102 Н/Кл | СИ: 56*10-9 Н - | Решение: 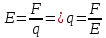 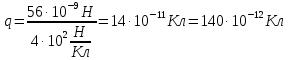 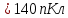 Элементарный заряд электрона: 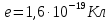 По формуле 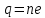 , выражаем n: , выражаем n: 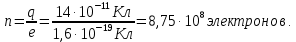 |
| Найти: q - ? n - ? | | Ответ: 140 пКл; 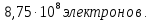 |
7. Чему равна напряженность поля, созданного зарядом +2 нКл в точке, удаленной от заряда на расстояние 10 см в воде?
| Дано: q = +2 нКл r = 10 см ε = 81 | СИ: 2*10-9 Кл 10-1 м | Решение: 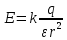 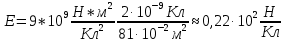 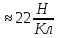 |
| Найти: E - ? | | Ответ: 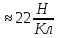 |
8. Чему равен потенциал в точке эквипотенциального поля, созданного зарядом +2 нКл в точке, удаленной от заряда на расстояние 10 см в воде?
| Дано: q = +2 нКл r = 10 см ε = 81 | СИ: 2*10-9 Кл 10-1 м | Решение: 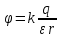 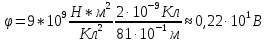 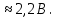 |
| Найти: φ - ? | | Ответ: 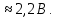 |
9. Две параллельные металлические пластины, расположенные на расстоянии 4 см. Потенциалы на верхних и нижних пластинах равны соответственно 2000 В и 800 В. Найдите напряженность однородного поля между пластинами. Чему равна работа по перемещению заряда, равного 20 мкКл. Вычислите электроемкость конденсатора.
| Дано: q = 20 мкКл d = 4 см φ1 = 2000 В φ2 = 800 В | СИ: 2*10-5 Кл 4*10-2 м - - | Решение: 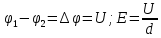 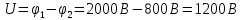 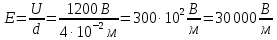 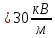 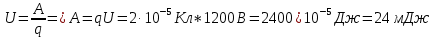 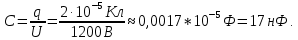 |
| Найти: E - ? A - ? C - ? | | Ответ: 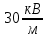 ; 24 мДж; 17 нФ. ; 24 мДж; 17 нФ. |
10. От каких факторов зависит электроемкость конденсатора?
1) От площади и формы обкладок
2) От расстояния между обкладками и удельного сопротивления их вещества
3) От наличия между обкладками диэлектрика и его цвета
4) От площади обкладок, расстояния между ними и наличия диэлектрика (т.к. это следует из формулы
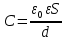 – электроемкость плоского конденсатора )
– электроемкость плоского конденсатора )Примеры решения задач на второй закон Ньютона в 10 классе
Пример 1.
Какую силу нужно приложить, чтобы магнит массой 70 г, прилипший к стальной вертикальной плите, равномерно переместить вертикально вверх? Для равномерного движения магнита вертикально вниз прикладывают силу 2,5 Н.
| №1. Дано: m = 70 г. Fт. = 2,5 Н g = 10 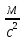 | SI: = 0,07 кг - - | Решение: По второму закону Ньютона, имеем действие сил на магнит (см. рисунок), сумма которых равна равнодействующей силе. Сначала в векторном виде 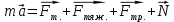 ; ;затем делаем проекции векторов на ось OX и ОY, направленная вниз т.к. магнит перемещается только по вертикали вниз – вдоль вертикальной плиты: ox: 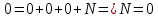 oy: 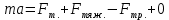 Там, где получились 0 – это значит, что между векторами и направлением осей угол 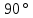 , а , а 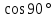 равен 0. равен 0. 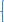 Составим систему уравнений: Составим систему уравнений: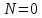 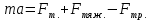 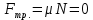 , т.к. , т.к. 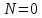 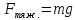 . .Теперь, мы можем найти 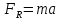 , учитывая из условия задачи, что движение и вниз, и вверх – равномерное, поэтому равнодействующая сила будет одинаковой по значению, что вниз, а значит, и вверх, т.к. движение равномерное. , учитывая из условия задачи, что движение и вниз, и вверх – равномерное, поэтому равнодействующая сила будет одинаковой по значению, что вниз, а значит, и вверх, т.к. движение равномерное.Итак, 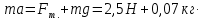 10 10 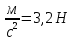 . .Это и все! |
| Найти: 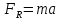 . - ? . - ? | 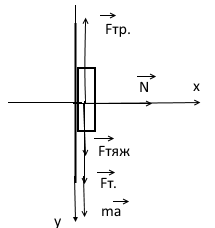 Рис. 9. Движение магнита вертикально вниз. | |
| Ответ: 3,2 Н. | | |