Примеры решения графических задач и действие сил, направленных вдоль одной прямой

Задача №1.

На рисунке 10 показано как измерили массу пустой мензурки, мензурки с жидкостью и мензурку с шариками, опущенными в жидкость.


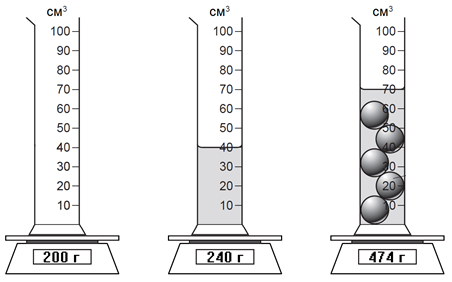
Рис. 10. Масса мензурки: пустой, с жидкостью и с шариками.

а) Определите плотность жидкости.
b) Найдите объем и массу одного шарика, а также плотность материала, из которого изготовлен шарик.

Дано:	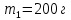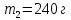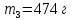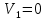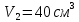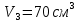СИ: - - - - - -	Решение: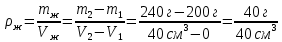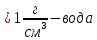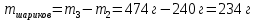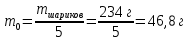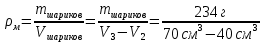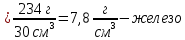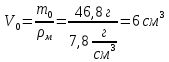
Найти:	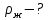	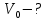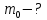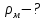Ответ: ; ; ; .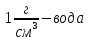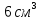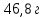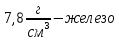

---

Задача №2.

На графике показана зависимость силы упругости от удлинения пружины.



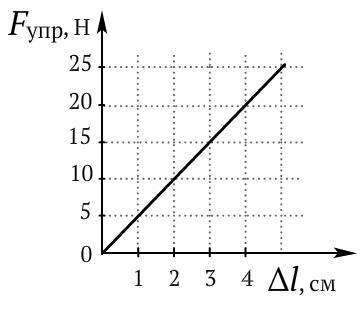
Рис. 11. График зависимости силы упругости от удлинения пружины.

Определите коэффициент жесткости k.

Дано: Fупр = 20 Н Δl =4 см	СИ: - 0,04 м	Решение: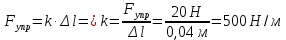
Найти: k - ?		Ответ: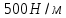

Задача №3

На движущийся автомобиль в горизонтальном направлении действует сила тяги двигателя 2,35 кН, сила трения 500 Н и сила сопротивления воздуха 335 Н. Чему равна равнодействующая этих сил?

Дано: Fт=2,35 кН Fтр=500 Н Fс=335 Н	СИ: = 2350 Н - -	Решение: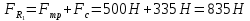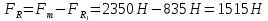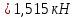
Найти: FR - ?		Ответ: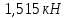

Рефлексия.

1. Какой пример решения задачи заинтересовал особенно?

2. Какой пример задачи вам знаком?

3. Какие задачи вызвали затруднения в понимании? Какие были просты?
2. Механические и электромагнитные колебания
2.1. Аналогия между механическими и электромагнитными колебаниями.

Цели: объяснение сути и доказательство аналогии между электромагнитными колебаниями и колебаниями пружинного маятника с использованием динамической колебательной модели ”Аналогия между механическими и электромагнитными колебаниями».

В пружинном маятнике упруго деформированная пружина сообщает скорость прикрепленному к ней грузу. Деформированная пружина обладает потенциальной энергией упругодеформированного тела :

---

,

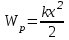движущийся груз обладает кинетической энергией .

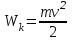Превращение потенциальной энергии пружины в кинетическую энергию колеблющегося тела является механической аналогией превращения энергии электрического поля конденсатора в энергию магнитного поля катушки. При этом аналогом механической потенциальной энергии пружины является энергия электрического поля конденсатора, а аналогом механической кинетической энергии груза является энергия магнитного поля, которая связана с движением зарядов. Зарядке конденсатора от батареи соответствует сообщение пружине потенциальной энергии (например, смещение рукой).

Сопоставим формулы и выведем общие закономерности для электромагнитных и механических колебаний.

ПРУЖИНА КОНДЕНСАТОР



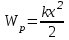
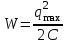
ГРУЗ КАТУШКА



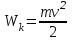
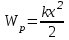
Из сопоставления формул следует, что аналогом индуктивности L является масса m, а аналогом смещения х служит заряд q, аналогом коэффициента k служит величина, обратная электроемкости, т. е. 1/С.

Моменту, кода конденсатор разрядится, а сила тока достигнет максимума, соответствует прохождение телом положения равновесия с максимальной скоростью.

Далее при перезарядке конденсатора тело будет смещаться влево от положения равновесия. Через промежуток времени, равный t=T/2, конденсатор полностью перезарядится и сила тока в цепи станет равной нулю.
Таблица №1. Аналогия между механическими и электромагнитными величинами

Механические величины	Электрические величины
Координата х	Заряд q
Скорость vx	Сила тока i
Масса m	Индуктивность L
Потенциальная энергия kx2/2	Энергия электрического поля q2/2С
Жесткость пружины k	Величина, обратная емкости 1/C
Кинетическая энергия mv2/2	Энергия магнитного поля Li2/2

---

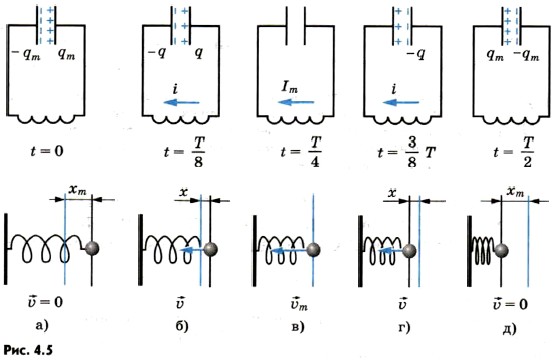
Рис. 12. Аналогия колебательных процессов в электромагнитных и механических природах взаимодействия.

Рефлексия.

1. В чём аналогия между механическими и электромагнитными колебаниями?

2. Какова аналогия в периодах превращения одного вида энергии в другой?
2.2. Колебательный контур. Формула Томсона.
Цель: описывать период и частоту электромагнитных колебаний и применять формулу Томсона при решении задач.
П 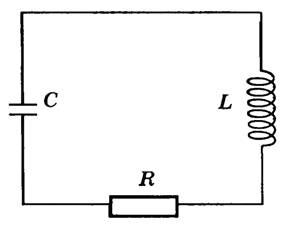од колебательным контуром обычно подразумевается устройство, состоящее из последовательно соединенных конденсатора, катушки индуктивности и резистора (наличие резистора возможно, но не обязательно).


Рис. 13. Колебательный контур.

Основной характеристикой конденсатора является его емкость C. В идеальном конденсаторе нет диссипативных потерь энергии. Его импеданс чисто реактивный. В реальных конденсаторах диэлектрик, заполняющий пространство между обкладками, может иметь небольшую электропроводность и поэтому возможны некоторые потери энергии на выделение джоулева тепла. Кроме того, при электрических колебаниях периодически происходит переполяризация диэлектрика, на которую также затрачивается некоторое количество энергии. В некоторых случаях приходится учитывать также тот факт, что кроме емкости C конденсатор, как и любой проводник, может иметь небольшое значение индуктивности L,

величина которой зависит от конструкции конденсатора. Основной характеристикой катушки индуктивности является ее индуктивность L.
Идеальная катушка, в которой нет потерь энергии, имеет чисто реактивный импеданс. Однако, если в катушке применяется сердечник, то при колебаниях в контуре часть энергии теряется на перемагничивание сердечника. Часть энергии теряется также на нагревание проводника обмотки, имеющей конечное значение сопротивления. Большое влияние на реальный импеданс катушки оказывают так называемые межвитковые емкости. Эти емкости имеют наименьшее значение в однослойных катушках с принудительным шагом (шаг спирали больше диаметра провода) и наибольшее в многослойных катушках с намоткой внавал.

Резисторы, кроме активного сопротивления R , могут иметь некоторое значение индуктивности.

---

В идеальном случае можно считать, что колебательный контур состоит из последовательно соединенных идеальных элементов L, R и C.
Теоретическая часть

Периодические изменения заряда q, силы тока I и напряжения U называют электрическими колебаниями. Свободные электрические гармоническое колебания происходят в колебательном контуре по закону:

q = q₀ cos (ωt + φ₀).

При свободных колебаниях происходит периодическое превращение электрической энергии, запасенной в конденсаторе, в магнитную энергию катушки, и наоборот. Полная электромагнитная энергия в идеальном колебательном контуре остается постоянной:



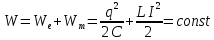
Собственная частота свободных колебаний равняется



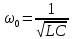
Период свободных колебаний равен:




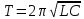
Колебания, возникающие в колебательной системе под действием периодически изменяющихся внешних сил, называются вынужденными.
Решение задач.

1. 
   Определить период колебаний в колебательном контуре, состоящем из катушки с индуктивностью 2·10^-4 Гн и конденсатора с емкостью 8 мкФ. Ответ дать в микросекундах.
   
2. 
   Определить электроемкость колебательного контура, индуктивность которого равна 200 Гн, а период колебаний 0,04 с. Принять квадрат числа «пи» равным 10. Ответ дать в микрофарадах.
   
3. 
   Индуктивность колебательного контура 20 мкГн. Какой конденсатор следует включить в контур, чтобы настроить его на частоту 5 МГц? Ответ выразить в пикофарадах. Принять квадрат числа «пи» равным 10.
   

Рефлексия.

1. Опишите зависимость между периодом и электроёмкостью конденсатора.

2. Объясните, как зависит частота от индуктивности катушки?

3. В чём особенность при решении задач на формулу Томсона?
2.4. Конденсатор в цепи переменного тока. Емкостное сопротивление.
Цель: объяснить роль конденсатора в цепи переменного тока и емкостного сопротивления.

---

Смотрите также файлы

• Страдательные причастия настоящего времени Повторение изученного.pptx

• 3 Криптографические методы защиты информации. (4 ак ч.) 3.docx

• Лекция использование цифровых технологий для индивидуализации обучения.docx

• Протокол 1 от августа 2022года Руководитель шмо О. С. Михайлюта Согласовано.docx

• Задание 1 Сформулируйте цели и задачи прохождения практики с учетом задач практики, установленных в программе практики, описав в отчете исходные данные, условия задачи и цели ее решения.docx