Файл: Контрольная работа Класс 8 класс Предмет Алгебра Тема Входная контрольная работа Цель.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 72
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Контрольная работа | |
| Класс | 8 класс |
| Предмет | Геометрия |
| Тема | Входная контрольная работа |
| Цель | Освоение дидактических единиц изученной темы и выявление учебных дефицитов. |
| Дидактические единицы | Смежные и вертикальные углы. Перпендикулярные прямые. Равнобедренный треугольник. Его свойства и признаки .Равносторонний треугольник Признаки равенства треугольников Окружность и круг. Центр, радиус, диаметр. Дуга, хорда. Параллельные и пересекающиеся прямые. Признаки параллельности двух прямых. |
| УУД, проверяемые в КР | Познавательные УУД: Соотносить предметные и метапредметные результаты деятельности. Личностные УУД: Смыслообразование Регулятивные УУД: контроль выполнения результата задания Коммуникативные УУД: корректировка действий |
| Критерии оценки: «5» «4» «3» «2» | Оценка задания: «5» все задания выполнены верно «4» правильно выполнены не менее ¾ задания «3» правильно выполнено не менее ½ задания «2» не выполнено более половины заданий. Отличная отметка не выставляется при наличии 3 исправлений |
| Содержание контрольной работы Вариант I. 1. Используя рисунок, найдите равнобедренные треугольники: 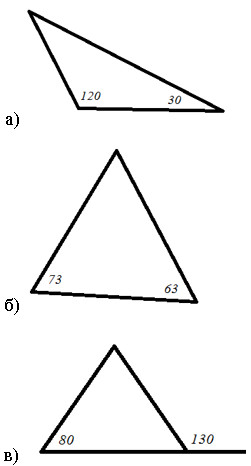 2. В равностороннем △ABC на биссектрисе ВН взята точка О так, что ON⊥BC; OM⊥AB (N∈BC, M∈AB). Докажите, что △AOM=△NOC. Найдите углы этих треугольников. 3. В окружности с центром в точке О хорды АВ и СD пересекаются в точке N. ∠CNB=150°; CD⊥OB; CO⊥AB. Найдите ∠COB. 4. Докажите, что если два отрезка равны и точкой пересечения делятся в одинаковом отношении, то отрезки, соединяющие концы данных отрезков, параллельны. Вариант II. 1. Используя рисунок, найдите равнобедренные треугольники: 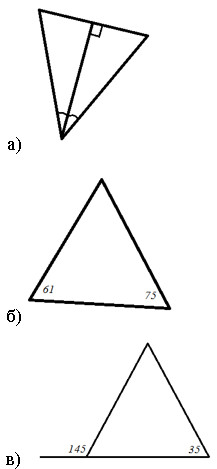 2. В равностороннем △ABC△ABC на высоте ВН взята точка О так, что ON⊥BC; OM⊥AB (N∈BC, M∈AB). Докажите, что △MOB=△NOB△MOB=△NOB. Найдите углы △ABC△ABC. 3. В окружности с центром в точке О хорды АВ и СD пересекаются в точке N. ∠AND=120°; CD⊥OB; CO⊥AB. Найдите ∠COB. 4. Докажите, что если два отрезка пересекаются в середине, то отрезки, соединяющие концы данных отрезков, параллельны. | |
| Контрольная работа | |
| Класс | 8 класс |
| Предмет | Геометрия |
| Тема | Контрольная работа по теме «Четырехугольники» |
| Цель | Освоение дидактических единиц изученной темы и выявление учебных дефицитов. |
| Дидактические единицы | Параллелограмм. Свойства параллелограмма. Признаки параллелограмма. Трапеция, свойства равнобедренной трапеции. Прямоугольник, его свойства. Ромб, его свойства. Квадрат и его свойства. |
| УУД, проверяемые в КР | Познавательные УУД: Соотносить предметные и метапредметные результаты деятельности. Личностные УУД: Смыслообразование Регулятивные УУД: контроль выполнения результата задания Коммуникативные УУД: корректировка действий |
| Критерии оценки: «5» «4» «3» «2» | Оценка задания: «5» все задания выполнены верно «4» правильно выполнены не менее ¾ задания «3» правильно выполнено не менее ½ задания «2» не выполнено более половины заданий. Отличная отметка не выставляется при наличии 3 исправлений |
| Содержание контрольной работы Вариант-1 № 1. Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360. Найдите угол AOD. № 2. Найдите углы прямоугольной трапеции, если один из его углов равен 200. № 3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма. № 4. В равнобедренной трапеции сумма углов при большем основании равна 960. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, АМ = 4 см. Найдите длину диагонали АD. Вариант-2. № 1. Диагонали прямоугольника MNKP пересекаются в точке О, ∟MОN=640. Найдите угол OMP. № 2. Найдите углы равнобедренной трапеции, если один из его углов на 300 больше другого. № 3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма. № 4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 480. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, длина диагонали АС равна 6 см. Найдите AМ, если точка М лежит на продолжении стороны AD. | |
| Контрольная работа | |
| Класс | 8 класс |
| Предмет | Геометрия |
| Тема | Контрольная работа по теме «Площадь» |
| Цель | Освоение дидактических единиц изученной темы и выявление учебных дефицитов. |
| Дидактические единицы | Понятие о площади плоских фигур и ее свойства. Единицы измерения площадей. Площадь прямоугольника Формула площади прямоугольника. Площадь параллелограмма. Формула площади параллелограмма. Площадь треугольника. Формула площади треугольника. Площадь ромба. Формула площади ромба. Площадь трапеции. Формула площади трапеции. Теорема Пифагора. |
| УУД, проверяемые в КР | Познавательные УУД: Соотносить предметные и метапредметные результаты деятельности. Личностные УУД: Смыслообразование Регулятивные УУД: контроль выполнения результата задания Коммуникативные УУД: корректировка действий |
| Критерии оценки: «5» «4» «3» «2» | Оценка задания: «5» все задания выполнены верно «4» правильно выполнены не менее ¾ задания «3» правильно выполнено не менее ½ задания «2» не выполнено более половины заданий. Отличная отметка не выставляется при наличии 3 исправлений |
| Содержание контрольной работы Вариант-1. № 1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. № 2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь этого треугольника. № 3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. № 4*. В прямоугольной трапеции АВСК большая боковая сторона равна 3√2 см, угол К равен 450, а высота СН делит основание АК пополам. Найдите площадь трапеции. Вариант-2. № 1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника. № 2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь этого треугольника. № 3. Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. № 4*. В прямоугольной трапеции АВСD большая боковая сторона равна 8 см, угол А равен 600, а высота ВН делит основание АD пополам. Найдите площадь трапеции. | |
| Контрольная работа | |
| Класс | 8 класс |
| Предмет | Геометрия |
| Тема | Контрольная работа по теме «Признаки подобия треугольников» |
| Цель | Освоение дидактических единиц изученной темы и выявление учебных дефицитов. |
| Дидактические единицы | Пропорциональные отрезки. Подобие трекгольников. Подобие треугольников, коэффициент подобия. Признаки подобия треугольников. |
| УУД, проверяемые в КР | Познавательные УУД: Соотносить предметные и метапредметные результаты деятельности. Личностные УУД: Смыслообразование Регулятивные УУД: контроль выполнения результата задания Коммуникативные УУД: корректировка действий |
| Критерии оценки: «5» «4» «3» «2» | Оценка задания: «5» все задания выполнены верно «4» правильно выполнены не менее ¾ задания «3» правильно выполнено не менее ½ задания «2» не выполнено более половины заданий. Отличная отметка не выставляется при наличии 3 исправлений |
| Содержание контрольной работы В 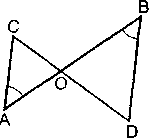 ариант-1. ариант-1. № 1. Рисунок 1 Дано: ∟А = ∟В, СО = 4, DО = 6, АО = 5. Найти: а) ОВ; б) АС : ВD; в) SAOC : SBOD. № 2. В треугольнике АВС АВ = 4 см, ВС= 7 см, АС = 6 см, а в треугольнике МNК МК = 8 см, МN =12 см, КN = 14 см. Найдите углы треугольника МNК, если ∟А = 80, ∟В = 600. № 3. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК ║АС, ВМ : АМ = 1: 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, А = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника АОD равна 45 см2. Вариант-2. № 1. Рисунок 1. Дано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6. Найти: а) МК; б) РЕ : NК; в) SМЕР : SMKN. 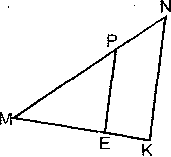 № 2. В ∆АВС АВ = 12 см, ВС = 18 см, ∟В = 700,а в ∆ МNК MN = 6 cм, NК = 9 см, ∟N= 700. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∟К = 600. № 3. Отрезки АВ и СD пересекаются в точке О так, что ∟АСО = =∟ВDО, АО : ОВ = 2 : 3. Найдите периметр треугольника АСО, если периметр треугольника ВОD равен 21 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, SAOD= 32 см2, S BOC = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см. | |
| Контрольная работа | |
| Класс | 8 класс |
| Предмет | Геометрия |
| Тема | Контрольная работа по теме «Подобие треугольников» |
| Цель | Освоение дидактических единиц изученной темы и выявление учебных дефицитов. |
| Дидактические единицы | Средняя линия треугольника. Свойство медиан треугольника. Пропорциональные отрезки. Определение пропорциональных отрезков. Решение задач с использованием теоремы Пифагора. |
| УУД, проверяемые в КР | Познавательные УУД: Соотносить предметные и метапредметные результаты деятельности. Личностные УУД: Смыслообразование Регулятивные УУД: контроль выполнения результата задания Коммуникативные УУД: корректировка действий |
| Критерии оценки: «5» «4» «3» «2» | Оценка задания: «5» все задания выполнены верно «4» правильно выполнены не менее ¾ задания «3» правильно выполнено не менее ½ задания «2» не выполнено более половины заданий. Отличная отметка не выставляется при наличии 3 исправлений |
| Содержание контрольной работы Вариант-1. № 1. Средние линии треугольника относятся как 2: 2: 4, а периметр треугольника равен 45 см. Найдите стороны треугольника. № 2. Медианы треугольника АВС пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите ЕF, если сторона АС равна 15 см. № 3. В прямоугольном треугольнике АВС (∟С= 900) АС = 5 см, ВС = 5√3 см. Найдите угол В и гипотенузу АВ. № 4. В треугольнике АВС ∟А =α, ∟С =β, сторона ВС = 7 см, ВН-высота. Найдите АН. № 5. В трапеции АВСD продолжения боковых сторон пересекаются в точке К, причем точка В-середина отрезка АК. Найдите сумму оснований трапеции, если АD = 12 см. Вариант-2. № 1. Средние линии треугольника относятся как 4: 5: 6, а периметр треугольника, образованного средними линиями, равен 30 см. Найдите средние линии треугольника. № 2. Медианы треугольника MNK пересекаются в точке О. Через точку О проведена прямая, параллельная стороне MK пересекающая стороны MN и NK в точках A и B соответственно. Найдите MK, если длина отрезка АB равна 12 см. №3. В прямоугольном треугольнике РКТ (∟Т= 900), РТ = 7√3 см, КТ= 7 см. Найдите угол К и гипотенузу КР. № 4. В треугольнике АВС ∟А =α, ∟С =β , высота ВН равна 4 см. Найдите АС. № 5. В трапеции MNKP продолжения боковых сторон пересекаются в точке E, причем EK=KP. Найдите разность оснований трапеции, если NK = 7 см. | |