Файл: Связи и массовых коммуникаций российской федерации федеральное государственное.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 209
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Коэффициент корреляции
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22 находим tкрит:
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22
tкрит(n-m-1;α/2) = tкрит(22;0.025) = 2.405
tнабл| > tкритич, полученное значение коэффициента корреляции признается значимым
Третья услуга – приобретение конвертов
у – период исследования
х3 – число приобретенных конвертов
| У | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Х3 | 21 | 8 | 5 | 6 | 6 | 6 | 6 | 6 |
| 21 | 9 | 5 | 7 | 6 | 7 | 7 | 7 | |
| 25 | 11 | 5 | 9 | 6 | 8 | 7 | 8 |
Коэффициент корреляции
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22 находим tкрит:
tкрит(n-m-1;α/2) = tкрит(22;0.025) = 2.405
tнабл| > tкритич, полученное значение коэффициента корреляции признается значимым
Четвертая услуга – приобретение открыток
у – период исследования
х4 – число приобретенных открыток.
| У | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Х4 | 14 | 8 | 5 | 6 | 6 | 6 | 6 | 6 |
| 24 | 9 | 5 | 8 | 6 | 7 | 7 | 7 | |
| 17 | 11 | 5 | 9 | 6 | 8 | 7 | 8 |
Коэффициент корреляции
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22 находим tкрит:
tкрит(n-m-1;α/2) = tкрит(22;0.025) = 2.405
tнабл| > tкритич, полученное значение коэффициента корреляции признается значимым
Пятая услуга – выдача бандеролей.
у – период исследования
х5 – число выданных бандеролей.
| У | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Х5 | 23 | 7 | 5 | 6 | 6 | 6 | 6 | 6 |
| 23 | 9 | 6 | 7 | 6 | 7 | 7 | 7 | |
| 33 | 10 | 5 | 9 | 6 | 8 | 7 | 8 |
Коэффициент корреляции
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=22 находим tкрит:
tкрит(n-m-1;α/2) = tкрит(22;0.025) = 2.405
tнабл| > tкритич, полученное значение коэффициента корреляции признается значимым
Составляем итоговую таблицу по расчетам коэффициента корреляции по каждой услуге:
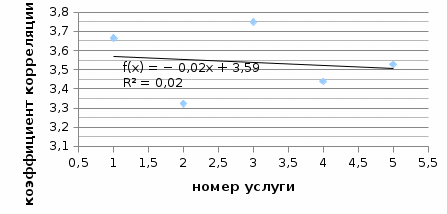
Рисунок 1 – Связь коэффициента корреляции от вида услуг
Связь коэффициентов корреляции между предприятиями с учетом вида услуг – линейная, обратно пропорциональная.
Задача 6
Известно, что максимальный размер коробки для почтовой посылки (тары) определяется величиной трех параметров: длиной (L), шириной (W) и высотой (H).
Известны ограничения: длина коробки (L) плюс периметр поперечного сечения не превосходят Е (см).
Е=L+2H+2W
L=2H=2W
L=E/3
Найти максимальный размер тары, если известны параметры.
Вычислить максимальное количество упаковочных коробок в 1 м3
Решение
По условию дано:
L=56 см.
Е=26500 см3
L=2H, следовательно H=W=56/2=28 см.
Объем коробки=56*28*28=43904 см3
1м =100 см
1м3=100*100*100=1000000 см3
Q=1000000/43904=23 коробки
Результаты представлены в таблице:
| L, см | Е, см3 | Н, см | W, см | Q в 1 м3 |
| 56 | 26500 | 28 | 28 | 23 |
Таким образом, в 1 м3, с установленными размерами почтовых коробок, количественная вместимость составит 23 коробки.
Задача 7
Имеется процесс, характеризующий работу телекоммуникационного узла связи. По результатам наблюдений создана аналитическая модель, отражающая некоторые особенности рабочих процессов.
Модель представлена серией выходных Y параметров.
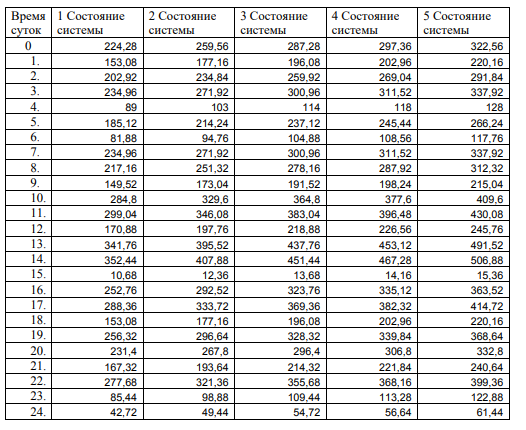
Определить:
-
Корреляцию первого процесса с остальными процессами; -
Вычислить дисперсию каждого процесса; -
Вычислить оценку подобия процессов.
Решение
состояние 1 системы – у.
состояние 2 системы – х1.
состояние 3 системы – х2.
состояние 4 системы – х3.
состояние 5 системы – х4.
Число наблюдений n = 25.
Число независимых переменных в модели равно 4
Исходные данные
| у | Х1 | Х2 | Х3 | Х4 |
| 224.28 | 259.56 | 287.28 | 297.36 | 322.56 |
| 153.08 | 177.16 | 196.08 | 202.96 | 220.16 |
| 202.92 | 234.84 | 259.92 | 269.04 | 291.84 |
| 234.96 | 271.92 | 300.96 | 311.52 | 337.92 |
| 89 | 103 | 114 | 118 | 128 |
| 185.12 | 214.24 | 237.12 | 245.44 | 266.24 |
| 81.88 | 94.76 | 104.88 | 108.56 | 117.76 |
| 234.96 | 271.92 | 300.96 | 311.52 | 337.92 |
| 217.16 | 251.32 | 278.16 | 287.92 | 312.32 |
| 149.52 | 173.04 | 191.52 | 198.24 | 215.04 |
| 284.8 | 329.6 | 364.8 | 377.6 | 409.6 |
| 299.04 | 346.08 | 383.04 | 396.48 | 430.08 |
| 170.88 | 197.76 | 218.88 | 226.56 | 245.76 |
| 341.76 | 395.92 | 437.76 | 453.12 | 491.52 |
| 352.44 | 407.88 | 451.44 | 467.28 | 506.88 |
| 10.68 | 12.36 | 13.68 | 14.16 | 15.36 |
| 252.76 | 292.52 | 323.76 | 335.12 | 363.52 |
| 288.36 | 333.72 | 369.36 | 382.32 | 414.72 |
| 153.08 | 177.16 | 196.08 | 202.96 | 220.16 |
| 256.32 | 296.64 | 328.32 | 339.84 | 368.64 |
| 231.4 | 267.8 | 296.4 | 306.8 | 332.8 |
| 167.32 | 193.64 | 214.32 | 221.84 | 240.64 |
| 277.68 | 321.36 | 355.68 | 368.16 | 399.36 |
| 85.44 | 98.88 | 109.44 | 113.28 | 122.88 |
| 42.72 | 49.44 | 54.72 | 56.64 | 61.44 |
Результаты предварительных расчетов:
| Признаки x и y | ∑xi | | ∑yi | | ∑xi*yi | |
| Для y и x1 | 5772.52 | 230.901 | 4987.56 | 199.502 | 1375641.387 | 55025.655 |
| Для y и x2 | 6388.56 | 255.542 | 4987.56 | 199.502 | 1522403.242 | 60896.13 |
| Для y и x3 | 6612.72 | 264.509 | 4987.56 | 199.502 | 1575820.899 | 63032.836 |
| Для y и x4 | 7173.12 | 286.925 | 4987.56 | 199.502 | 1709365.043 | 68374.602 |
| Для x1 и x2 | 6388.56 | 255.542 | 5772.52 | 230.901 | 1762057.507 | 70482.3 |
| Для x1 и x3 | 6612.72 | 264.509 | 5772.52 | 230.901 | 1823884.086 | 72955.363 |
| Для x1 и x4 | 7173.12 | 286.925 | 5772.52 | 230.901 | 1978450.534 | 79138.021 |
| Для x2 и x3 | 6612.72 | 264.509 | 6388.56 | 255.542 | 2018467.219 | 80738.689 |
| Для x2 и x4 | 7173.12 | 286.925 | 6388.56 | 255.542 | 2189523.763 | 87580.951 |
| Для x3 и x4 | 7173.12 | 286.925 | 6612.72 | 264.509 | 2266349.158 | 90653.966 |
Найдем парные коэффициенты корреляции.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x1 и y.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x2 и y.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x3 и y.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x4 и y.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x2 и x1.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x3 и x1.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x4 и x1.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x3 и x2.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x4 и x2.