Файл: Связи и массовых коммуникаций российской федерации федеральное государственное.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 210
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x4 и x3.
Результаты расчетов дисперсии:
| Признаки x и y | | |
| Для y и x1 | 10372.532 | 7740.508 |
| Для y и x2 | 12699.866 | 7740.508 |
| Для y и x3 | 13606.72 | 7740.508 |
| Для y и x4 | 16010.665 | 7740.508 |
| Для x1 и x2 | 12699.866 | 10372.532 |
| Для x1 и x3 | 13606.72 | 10372.532 |
| Для x1 и x4 | 16010.665 | 10372.532 |
| Для x2 и x3 | 13606.72 | 12699.866 |
| Для x2 и x4 | 16010.665 | 12699.866 |
| Для x3 и x4 | 16010.665 | 13606.72 |
Оценка подобия дисперсий
Находим групповые средние:
| N | П1 | П2 |
| 1 | 10372.532 | 7740.508 |
| 2 | 12699.866 | 7740.508 |
| 3 | 13606.72 | 7740.508 |
| 4 | 16010.665 | 7740.508 |
| 5 | 12699.866 | 10372.532 |
| 6 | 13606.72 | 10372.532 |
| 7 | 16010.665 | 10372.532 |
| 8 | 13606.72 | 12699.866 |
| 9 | 16010.665 | 12699.866 |
| 10 | 16010.665 | 13606.72 |
| ∑ | 140635.084 | 101086.08 |
| xср | 14063.508 | 10108.608 |
Общая средняя дисперсия:
| N | П21 | П22 |
| 1 | 107589420.09102 | 59915464.098064 |
| 2 | 161286596.41796 | 59915464.098064 |
| 3 | 185142829.1584 | 59915464.098064 |
| 4 | 256341393.74223 | 59915464.098064 |
| 5 | 161286596.41796 | 107589420.09102 |
| 6 | 185142829.1584 | 107589420.09102 |
| 7 | 256341393.74223 | 107589420.09102 |
| 8 | 185142829.1584 | 161286596.41796 |
| 9 | 256341393.74223 | 161286596.41796 |
| 10 | 256341393.74223 | 185142829.1584 |
| ∑ | 2010956675.371 | 1070146138.6596 |
Sобщ = 2010956675.371 + 1070146138.6596 - 10 • 2 • 12086.062 = 159646757.75
Sф = 10(14063.512 + 10108.612 - 2 • 12086.062) = 78206185.87
Sост: Sост = Sобщ - Sф = 159646757.75 - 78206185.87 = 81440571.89
Определяем факторную дисперсию:
остаточную дисперсию:
Оценка факторной дисперсии больше оценки остаточной дисперсии.
Находим fнабл.
Для уровня значимости α=0.05, чисел степеней свободы 1 и 18 находим fкр из таблицы распределения Фишера-Снедекора.
fкр(0.05; 1; 18) = 4.41
Групповые средние в целом различаются значимо.
Задача 8
Имеет набор систем, таких, что кластер характеризуется функцией выхода:
| № | 1 | 2 | 3 | 4 | 5 | 6 |
| w | 152.3 | 1800.2 | 42.1 | 15.8 | 15234 | 425 |
| a | 14.8 | 47.85 | 28.3 | 14.8 | 47.85 | 28.3 |
Найти:
функция выхода:
| № | 1 | 2 | 3 | 4 | 5 | 6 |
| w | 152.3 | 1800.2 | 42.1 | 15.8 | 15234 | 425 |
| a | 14.8 | 47.85 | 28.3 | 14.8 | 47.85 | 28.3 |
С учетом данных и наложенных условий по заданию функция выхода примет следующий вид:
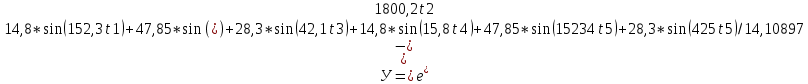
Проведем кластерный анализ.
В качестве расстояния между объектами примем обычное евклидовое расстояние:
где l - признаки; k - количество признаков
Составляем матрицу расстояний:

| 0 | 1648.231 | 111.024 | 136.5 | 15081.736 | 273.034 |
| 1648.231 | 0 | 1758.209 | 1784.706 | 13433.8 | 1375.339 |
| 111.024 | 1758.209 | 0 | 29.562 | 15191.913 | 382.9 |
| 136.5 | 1784.706 | 29.562 | 0 | 15218.236 | 409.423 |
| 15081.736 | 13433.8 | 15191.913 | 15218.236 | 0 | 14809.013 |
| 273.034 | 1375.339 | 382.9 | 409.423 | 14809.013 | 0 |
Минимизация расстояний: объекты 3 и 4 наиболее близки P3;4 = 29.56 и поэтому объединяются в один кластер.
| | 1 | 2 | [3] | [4] | 5 | 6 |
| 1 |  0 0 | 1648.231 | 111.024 | 136.5 | 15081.736 | 273.034 |
| 2 | 1648.231 | 0 | 1758.209 | 1784.706 | 13433.8 | 1375.339 |
| [3] | 111.024 | 1758.209 | 0 | 29.562 | 15191.913 | 382.9 |
| [4] | 136.5 | 1784.706 | 29.562 | 0 | 15218.236 | 409.423 |
| 5 | 15081.736 | 13433.8 | 15191.913 | 15218.236 | 0 | 14809.013 |
| 6 | 273.034 | 1375.339 | 382.9 | 409.423 | 14809.013 | 0 |
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №3 и №4.
В результате имеем 5 кластеров: S(1), S(2), S(3,4), S(5), S(6)
Из матрицы расстояний следует, что объекты 1 и 3,4 наиболее близки P1;3,4 = 111.02 и поэтому объединяются в один кластер.
| | [1] | 2 | [3,4] | 5 | 6 |
| [1] |  0 0 | 1648.231 | 111.024 | 15081.736 | 273.034 |
| 2 | 1648.231 | 0 | 1758.209 | 13433.8 | 1375.339 |
| [3,4] | 111.024 | 1758.209 | 0 | 15191.913 | 382.9 |
| 5 | 15081.736 | 13433.8 | 15191.913 | 0 | 14809.013 |
| 6 | 273.034 | 1375.339 | 382.9 | 14809.013 | 0 |
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №1 и №3,4.
В результате имеем 4 кластера: S(1,3,4), S(2), S(5), S(6)
Из матрицы расстояний следует, что объекты 1,3,4 и 6 наиболее близки P1,3,4;6 = 273.03 и поэтому объединяются в один кластер.
| | [1,3,4] | 2 | 5 | [6] |
| [1,3,4] |  0 0 | 1648.231 | 15081.736 | 273.034 |
| 2 | 1648.231 | 0 | 13433.8 | 1375.339 |
| 5 | 15081.736 | 13433.8 | 0 | 14809.013 |
| [6] | 273.034 | 1375.339 | 14809.013 | 0 |
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №1,3,4 и №6.
В результате имеем 3 кластера: S(1,3,4,6), S(2), S(5)
Из матрицы расстояний следует, что объекты 1,3,4,6 и 2 наиболее близки P1,3,4,6;2 = 1375.34 и поэтому объединяются в один кластер.
| | [1,3,4,6] | [2] | 5 |
| [1,3,4,6] |  0 0 | 1375.339 | 14809.013 |
| [2] | 1375.339 | 0 | 13433.8 |
| 5 | 14809.013 | 13433.8 | 0 |
При формировании новой матрицы расстояний, выбираем наименьшее значение из значений объектов №1,3,4,6 и №2.
В результате имеем 2 кластера: S(1,3,4,6,2), S(5)
| | 1,3,4,6,2 | 5 |
| 1,3,4,6,2 | 0 | 13433.8 |
| 5 | 13433.8 | 0 |