Файл: Метод рационализации (замена множителей) при решении неравенств.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Метод рационализации (замена множителей)
при решении неравенств
Решение неравенств, содержащих модули, корни, логарифмические, показательные функции или их комбинацию стандартными школьными методами часто оказывается сложными и громоздкими, что вызывает определенные трудности.
Одним из эффективных и доступных методов решения таких неравенств и их систем является метод рационализации, базирующийся на концепции равносильности математических высказываниях.
Два неравенства A и B называются равносильными на множестве M, если множества их решений совпадают. Замена одного неравенства другим, равносильным данному на M, называется равносильным преобразованием на M.
Если функция f(x) строго возрастает, то знак выражения f(x1) - f(x2) совпадает со знаком выражения x1- x2. Если функция f(x) строго убывает, то знак выражения f(x1) - f(x2) совпадает со знаком выражения x2- x1.
Этот факт можно использовать при решении неравенств, в правой части которых стоит ноль. Можно в левой части (числителе и/или знаменателе левой части) заменить разность значений монотонной функции разностью значений аргумента. При этом, если функция возрастающая, то знак неравенства сохраняется, а если функция убывающая, то знак неравенства заменяется на противоположный.
При условии неизменности знака решаемого неравенства множители, принимающие положительные значения можно просто исключить, а множители, принимающие отрицательные значения – заменить на (-1).
Метод позволяет упростить неравенство, сведя его решение к решению более простого неравенства или системы более простых неравенств. Решение последних легко осуществляется методом для рациональных функций.
Таким образом, суть метода в том, что в неравенстве можно перейти от сложного выражения к более простому. Такой переход допустим, если выполнены условия:
1) Обязательно нужно учесть ОДЗ изначальных функций;
2) Делать замену можно только если с одной стороны неравенства стоит 0:
3) Неравенство привести к виду
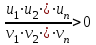 (<; ; ).
(<; ; ).При решении задачи исходное неравенство преобразуется в систему: рационализированное неравенство и ОДЗ исходного неравенства.
Неравенства, содержащие модуль
| Выражение с модулями | Замена |
| f | f2 |
| f - g | f2 - g2 = (f – g)(f + g) |
| f - g | (f – g)(f + g), g 0 |
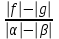 | 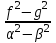 |
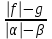 | 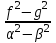 , (g 0, 0) , (g 0, 0) |
| (f - g)( - ) | (f2 - g2)(2 - 2) |
1) x - 1 < 2
Замена множителей: x - 1 - 2 < 0 (x – 1)2 – 22 < 0, (x – 1 – 2)(x – 1 + 2) < 0
(x – 3)(x+ 1) < 0, -1< х < 3. Отв. (-1; 3).
2) (x - 1 - 3)(x + 2 - 5) < 0.
(x - 1 - 3)(x + 2 - 5) < 0 ((x – 1)2 - 32)((x + 2)2 - 52) < 0,
(x – 1 - 3)(x - 1 + 3)(x + 2 - 5)(x + 2 + 5) < 0, (x – 4)(x + 2)(x - 3)(x + 7) < 0
Отв. (-7; -2)(3; 4).

3) x - 1 - 5 2.
x - 1 - 5 - 2 0 (x - 1 - 5)2 - 22 0, (x - 1 - 7)(x - 1 - 3) 0
(x - 8)(x + 6)(x - 4)(x + 2) 0
Отв. -6; -24; 8.

4) x2 – 7x + 2 x2 + 5x - 2.
x2 – 7x + 2 x2 + 5x - 2, x2 – 7x + 2 - x2 + 5x - 2 0 (x2 – 7x + 2)2 – (x2 + 5x – 2)2 0, (x2 – 7x + 2 - x2 - 5x + 2)(x2 – 7x + 2 + x2 + 5x - 2) 0,
(-12x + 4)(2x2 - 2x) 0, (3x - 1)(x - 1)x 0
Отв. 0; 1/31; ).
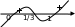
5)
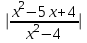 1.
1.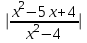 - 1 0
- 1 0 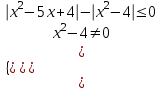 ;
; 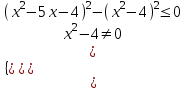
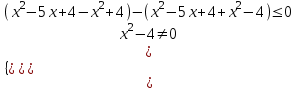 ;
; 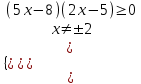
Отв. 0; 1,62,5; ).
6)
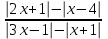 0
0 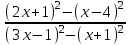 0,
0, 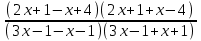 0,
0, 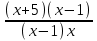 0
0 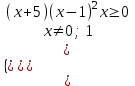
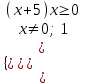
Отв. (-; -5(0; 1)(1; ).
7)
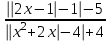 0
0 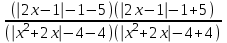 0
0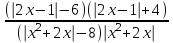 0
0 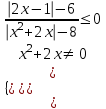
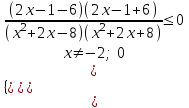 ,
, 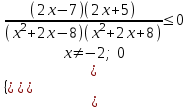
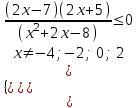 ,
, 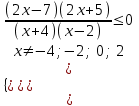
Отв. (-4; -2,5(2; 3,5.
8)
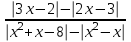 0
0 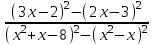 0,
0, 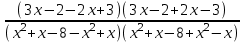 0,
0, 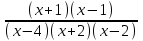 0
0 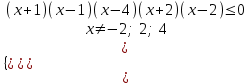 , х(-; -2)-1; 1(2; 4)
, х(-; -2)-1; 1(2; 4)Отв. (-; -2)-1; 1(2; 4).
9) 2x2 - x - 3 - (2x2 + x + 5) 0. Т.к. 2x2 + x + 5 > 0 при всех xR, то исходное неравенство равносильно неравенству: (2x2 - x - 3)2 - (2x2 + x + 5)2 0,
(2x - x - 3 - 2x2 - x - 5)(2x - x - 3 + 2x2 + x + 5) 0,
(2x2 - x - (2x2 + x - 8)(2x2 - x + 2x2 + x + 2) 0
и т.к. 2x2 - x + 2x2 + x + 2 > 0 при всех xR, то
(2x2 - x - (2x2 + x - 8) 0 ((2x2 - x)2 - (2x2 + x - 8)2 0
(2x2 - x - 2x
2 - x - 8)(2x2 - x + 2x2 + x + 8) 0, (x + 4)(x2 + 8) 0, (x + 4) 0
x -4. Отв. -4; ).
10)
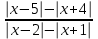 <
< 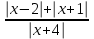 .
.Умножим обе части неравенства на функцию
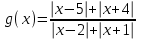 , g(x) >0 xR
, g(x) >0 xR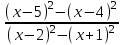 <
< 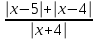 ,
, 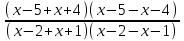 <
< 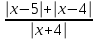 ,
, 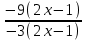 <
< 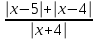
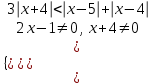 ,
, 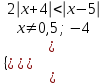
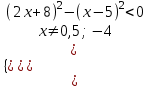 ,
, 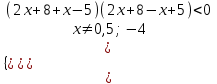
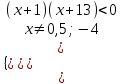 . Отв. (-13; -4)(-4; -1).
. Отв. (-13; -4)(-4; -1).11) 5x2 - 6x - 8 3x2 - 4x + 4
(5x2 - 6x - 8 - 3x2 + 12x - 12)(5x2 - 6x - 8 + 3x2 - 12x + 12) 0
(2x2 + 6x - 20) (8x2 - 18x + 4) 0, (x2 + 3x - 10) (4x2 - 9x + 2) 0,
(x +5)(x -2)(4x -1)(x - 2) 0, (x -2)2(4x -1) 0
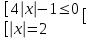
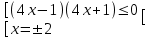 x-2-0,25; 0,252
x-2-0,25; 0,252Отв. -2-0,25; 0,252
Иррациональные неравенства
| Выражение с корнями | Замена |
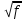 | f 2 |
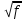 - - 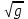 | f – g, (f 0, g 0) |
| f - 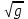 | f 2 – g, (f 0, g 0) |
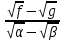 | 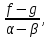 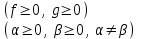 |
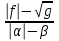 | 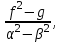 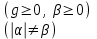 |
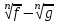 | f – g, (f 0, g 0) |
| Выражение с модулями и корнями | Замена |
| f | f 2 |
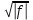 | f 2 |
| f -  | f 2 – g, (g 0) |
 - - 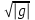 | f 2 – g2, (f 0) |
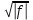 - g - g | (f – g2) (f + g2), (g 0) |
| f - 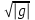 | (f 2– g) (f 2+ g) |
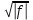 - -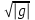 | (f – g) (f + g) |
1) (x – 3)
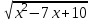 0.
0. (x – 3)
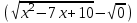 0.
0. Можно заменить разность значений корня разностью подкоренных выражений. При этом необходимо учесть область определения арифметического квадратного корня.

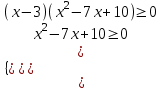 ;
; 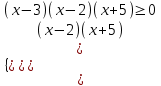
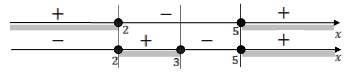
Отв. 25; )
2)
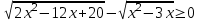 .
.Заменим неравенство равносильной системой, используя метод рационализации
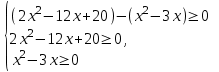 ;
; 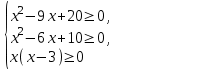
а)
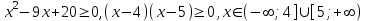
б