Файл: Метод рационализации (замена множителей) при решении неравенств.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 31
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
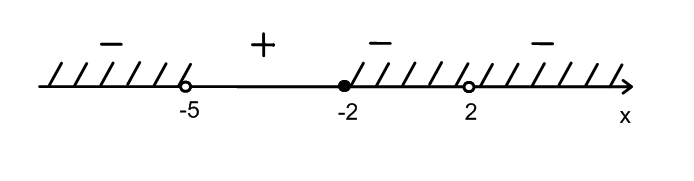
x-2; 2)(2; ). Отв. -2; 2)(2; )
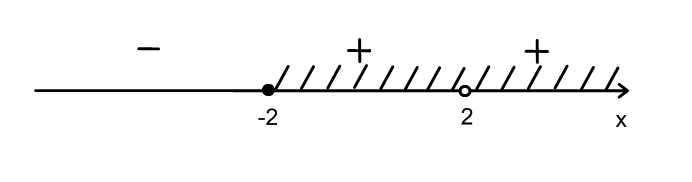
9)
.
, 
,
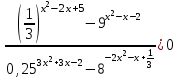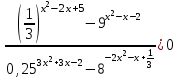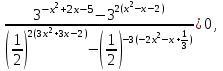
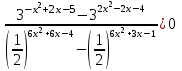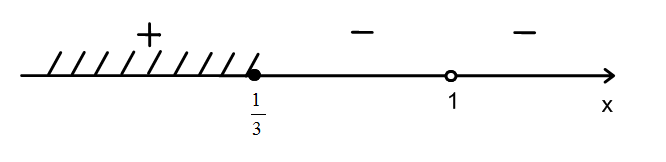
Решим неравенство, используя метод рационализации
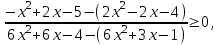
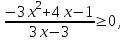
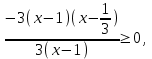
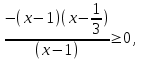
x 1/3. Отв. (-; 1/3
10)
.
, 
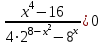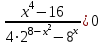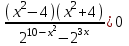
Решим неравенство, используя метод рационализации
, 
, 
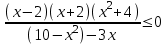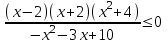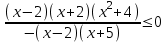
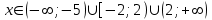
Ответ: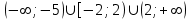
Логарифмические неравенства
1) log0,5(x2 – 3x + 2) + 1 0, -log2(x2 – 3x + 2) + log22 0,
log2(x2 – 3x + 2) - log22 0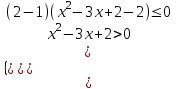 
х0; 1)(2; 3.
2)
.
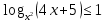ОДЗ: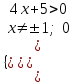
, 
, 
,
; 
; 
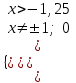
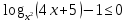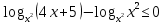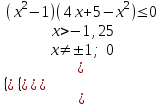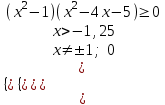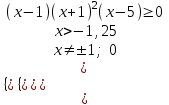х(-1,25; -1)(-1; 0)(0; 1)5; ).
3)
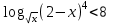
ОДЗ: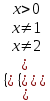
, х(0; 1)(1; 2)(2; ).
, 
, 
(
)(
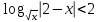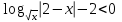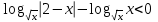
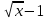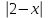- x) < 0, (x - 1)(2 – x - x)(2 – x + x) < 0, (x - 1)2 > 0 x ≠ 1
С учетом ОДЗ запишем ответ. Отв. (0; 1)(1; 2)(2; ).
4)
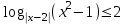
ОДЗ: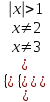
, х(-;-1)(1; 2)(2; 3)(3; ).
, 
,
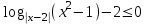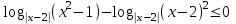(x- 2 - 1)(x2 – 1 – x2 + 4x - 4) 0, (x - 3)(x - 1)(4x + 5) 0
х(-;-11,25; 3. С учетом ОДЗ запишем ответ.
Отв. (-;-1)1,25; 2)(2; 3).
5) x∙logx+3(2x + 7) 0
ОДЗ: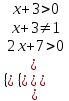
,
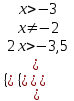, х(-3; -2)(-2; ).
x(logx+3(2x + 7) - logx+31) 0, x(x + 3 -1)(2x + 7 - 1) 0,
x(x + 2)(x + 3) 0 х-3;-20; ). С учетом ОДЗ запишем ответ.
Отв. (-3; -2)0; ).
6)
.
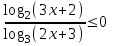ОДЗ: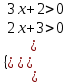
, 
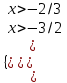, х > -2/3.
Применим метод рационализации.
, 
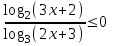
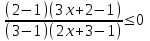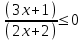
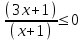
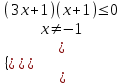х(-1;-1/3.
С учетом ОДЗ, получим х(-2/3;-1/3.
7)
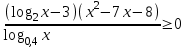
Приведем неравенство к виду, в котором явно видна разность значений логарифмической функции.
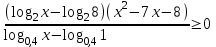. Заменим разность значений логарифмической функции на разность значений аргумента. В числителе функция возрастающая, а в знаменателе убывающая, поэтому знак неравенства изменится на противоположный. Важно не забывать область определения логарифмической функции, поэтому данное неравенство равносильно системе неравенств
; 
, 
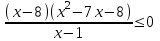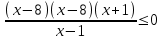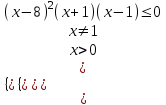
Решая неравенство методом интервалов, получим ответ
Отв. (0; 1)8.
8)
.
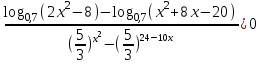ОДЗ: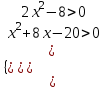
; 
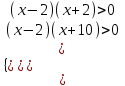(x - 2)2(x + 2)(x + 10) > 0
х(-; -10)(-2; 2)(2; ).
Заменим в числителе и знаменателе разность значений монотонных функций разностью значений аргументов, учитывая область определения функций и характер монотонности.
ОДЗ: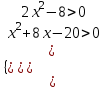 ; 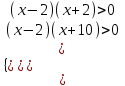(x - 2)2(x + 2)(x + 10) > 0
х(-; -10)(-2; 2)(2; ).
, 
, 
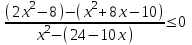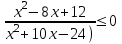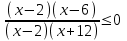
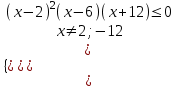х(-12; 2)(2; 6.
Объединяя с ОДЗ, получим ответ. Отв. (-12; -10)(2; 6.
9)
, 
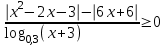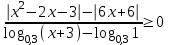
ОДЗ: x + 3 > 0, x > -3, х(-3; ).
Заменим в числителе разность модулей двух функций разностью квадратов, а в знаменателе разность значений логарифмических функций разностью аргументов. В знаменателе функция убывающая, знак неравенства изменяется на противоположный. При этом надо учесть область определения логарифмической функции.
, 
,
, 
,
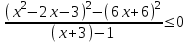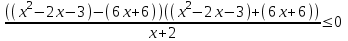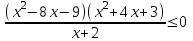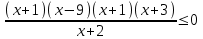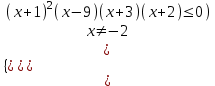х(-;-3)(-2; 9.
Объединяя с ОДЗ, получим ответ. Отв. (-2; 9.
10) logx(x3 +1)∙logx+1x >2,
ОДЗ: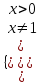
11)
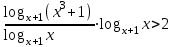, logx+1(x3 +1) - 2 > 0,
logx+1(x3 +1) - logx+1(x + 1)2 > 0, (x + 1 - 1)( x3 +1 – x2 - 2x - 1) > 0,
( x3 +1 – x2 -2x - 1) > 0, x2(x2 - x - 2) > 0, x2(x + 1)(x - 2) > 0
x(-;-1)(2; ). Учитывая ОДЗ, получим x >2. Отв. (2; ).
9)
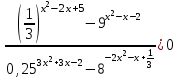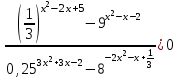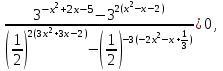
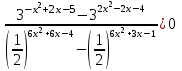. , , Решим неравенство, используя метод рационализации
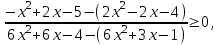
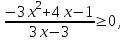
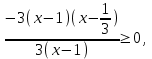
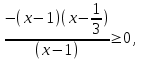
x 1/3. Отв. (-; 1/3
10)
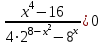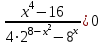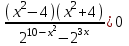
. , Решим неравенство, используя метод рационализации
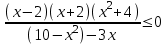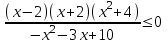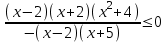
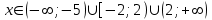
, , Ответ:
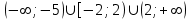
Логарифмические неравенства
| Выражение | Замена |
| logaf(x) - logag(x) | (a – 1)(f(x) – g(x)), (a > 0, a 1) |
| logaf(x) + logag(x) | (a – 1)(f(x)∙g(x) - 1), (a > 0, a 1) |
| logaf(x) – b | (a – 1)(f(x) - ab), (a > 0, a 1) |
| logaf(x) + b | (a – 1)(f(x)∙ab - 1), (a > 0, a 1) |
| loga(x)f(x) - loga(x)g(x) | (a(x) –1)(f(x) – g(x)), (a(x) > 0, a(x) 1) |
| logaf(x) – 1 | (a – 1)(f(x) - a), (a > 0, a 1) |
| logaf(x) | (a – 1)(f(x) - 1), (a > 0, a 1) |
 |  |
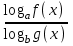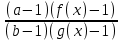| logaf(x)∙logbg(x) | (a – 1)(f(x) - 1)(b – 1)(g(x) - 1) |
| loga1(x)f(x)∙loga2(x)f(x) (a1(x) ≠ 1, a2(x) ≠ 1) | (a1(x) – 1)(a2(x) – 1)(f(x) - 1)(a2(x) – a1(x)) |
1) log0,5(x2 – 3x + 2) + 1 0, -log2(x2 – 3x + 2) + log22 0,
log2(x2 – 3x + 2) - log22 0
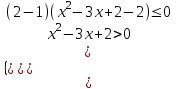
х0; 1)(2; 3.2)
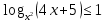. ОДЗ:
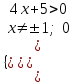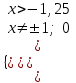
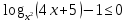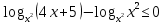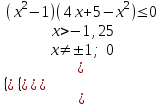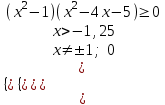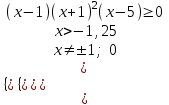, , , ; ; х(-1,25; -1)(-1; 0)(0; 1)5; ).3)
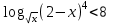
ОДЗ:
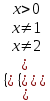, х(0; 1)(1; 2)(2; ). , , (
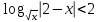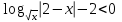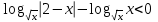
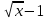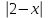)( - x) < 0, (x - 1)(2 – x - x)(2 – x + x) < 0, (x - 1)2 > 0 x ≠ 1 С учетом ОДЗ запишем ответ. Отв. (0; 1)(1; 2)(2; ).
4)
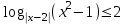
ОДЗ:
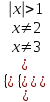, х(-;-1)(1; 2)(2; 3)(3; ). 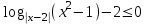, , 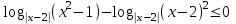(x- 2 - 1)(x2 – 1 – x2 + 4x - 4) 0, (x - 3)(x - 1)(4x + 5) 0
х(-;-11,25; 3. С учетом ОДЗ запишем ответ.
Отв. (-;-1)1,25; 2)(2; 3).
5) x∙logx+3(2x + 7) 0
ОДЗ:
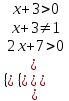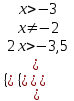, , х(-3; -2)(-2; ).x(logx+3(2x + 7) - logx+31) 0, x(x + 3 -1)(2x + 7 - 1) 0,
x(x + 2)(x + 3) 0 х-3;-20; ). С учетом ОДЗ запишем ответ.
Отв. (-3; -2)0; ).
6)
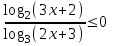. ОДЗ:
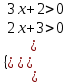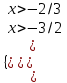, , х > -2/3.Применим метод рационализации.
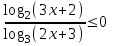
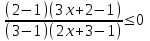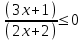
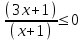
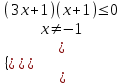, х(-1;-1/3.С учетом ОДЗ, получим х(-2/3;-1/3.
7)
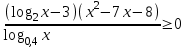
Приведем неравенство к виду, в котором явно видна разность значений логарифмической функции.
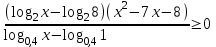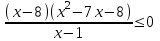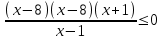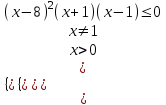
. Заменим разность значений логарифмической функции на разность значений аргумента. В числителе функция возрастающая, а в знаменателе убывающая, поэтому знак неравенства изменится на противоположный. Важно не забывать область определения логарифмической функции, поэтому данное неравенство равносильно системе неравенств ; , Решая неравенство методом интервалов, получим ответ
Отв. (0; 1)8.
8)
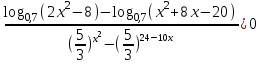.ОДЗ:
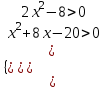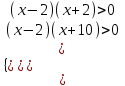; (x - 2)2(x + 2)(x + 10) > 0х(-; -10)(-2; 2)(2; ).
Заменим в числителе и знаменателе разность значений монотонных функций разностью значений аргументов, учитывая область определения функций и характер монотонности.
ОДЗ:
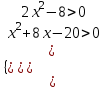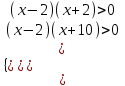; (x - 2)2(x + 2)(x + 10) > 0х(-; -10)(-2; 2)(2; ).
, ,
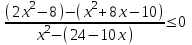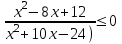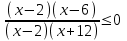
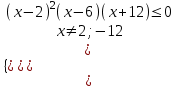х(-12; 2)(2; 6.Объединяя с ОДЗ, получим ответ. Отв. (-12; -10)(2; 6.
9)
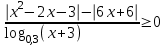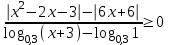
, ОДЗ: x + 3 > 0, x > -3, х(-3; ).
Заменим в числителе разность модулей двух функций разностью квадратов, а в знаменателе разность значений логарифмических функций разностью аргументов. В знаменателе функция убывающая, знак неравенства изменяется на противоположный. При этом надо учесть область определения логарифмической функции.
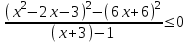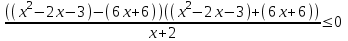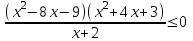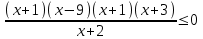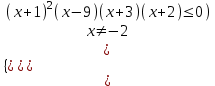, , , , х(-;-3)(-2; 9.Объединяя с ОДЗ, получим ответ. Отв. (-2; 9.
10) logx(x3 +1)∙logx+1x >2,
ОДЗ:
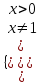
11)
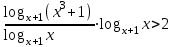, logx+1(x3 +1) - 2 > 0, logx+1(x3 +1) - logx+1(x + 1)2 > 0, (x + 1 - 1)( x3 +1 – x2 - 2x - 1) > 0,
( x3 +1 – x2 -2x - 1) > 0, x2(x2 - x - 2) > 0, x2(x + 1)(x - 2) > 0
x(-;-1)(2; ). Учитывая ОДЗ, получим x >2. Отв. (2; ).