Файл: Метод рационализации (замена множителей) при решении неравенств.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 30
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
) 
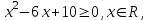
в)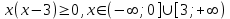
Решение исходного неравенства:
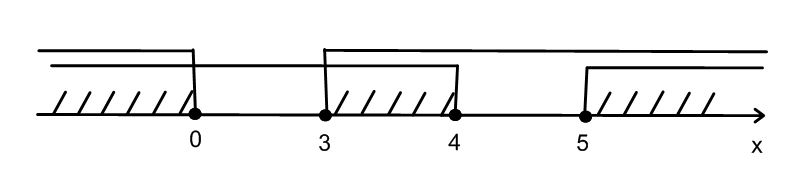
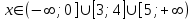
Ответ: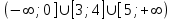
3)
.
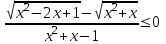Заменим неравенство равносильной системой, используя метод рационализации
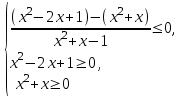
а)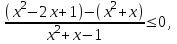
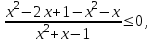
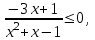
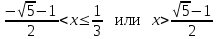
б)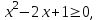
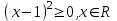
в)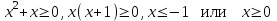
Решение исходного неравенства:
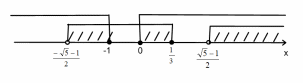
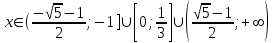
Ответ: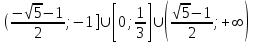
4)
.
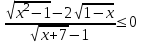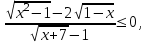
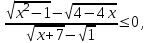
Заменим неравенство равносильной системой, используя метод рационализации
; 
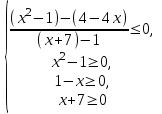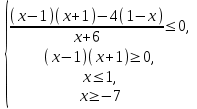
а)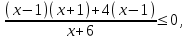
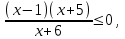
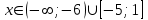
б)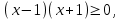
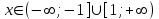
Решение исходного неравенства:
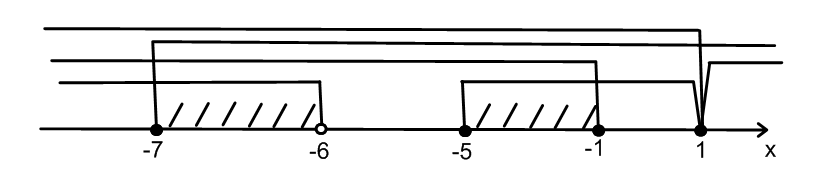
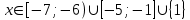. Ответ: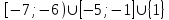
5)
.
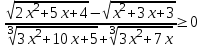Т.к. 2x2 + 5x + 4 > 0 и x2 + 3x + 3 > 0 при всех х, то
, 
, 
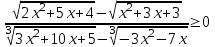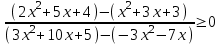
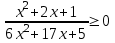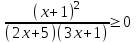
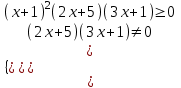
Отв. (-∞; -5/2)-1(-1/3; ∞).
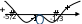
6) Найти сумму целых значений x, удовлетворяющих неравенству
(x + 3)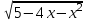
0.
Рассмотрим, сначала, уравнение
(x + 3)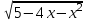 = 0
и найдем его корни:
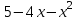= 0, x2 + 4x – 5 = 0, (x + 5)(x - 1) = 0, x1 = -5, x2 = 1.
x + 3 = 0, x3 = -3
Отсюда, в частности, вытекает, что область определения исходного неравенства имеет вид x-5; 1.
Рассмотрим теперь строгое неравенство
(x + 3)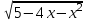 < 0.
В этом случае, в силу того, что квадратный корень положителен, выполняется неравенство
x + 3 < 0, x < -3,
откуда, воспользовавшись x-5; 1, получаем, что, решение исходного неравенства имеет вид:
x-5; -31
Для завершения решения задачи остается заметить, что в множество
-5; -31входят целые числа: -5, -4, -3, 1 , сумма которых равна -11.
Отв. -11.
7) Найти сумму всех целых чисел, являющихся решением неравенства
.
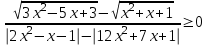Т.к. 3x2 - 5x + 3 > 0 и x2 + x + 1 > 0 при всех х, то
, 
.
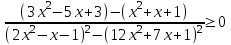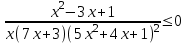Т.к. 5x2 + 4x + 1 > 0 при всех х, то
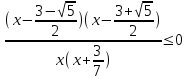x(-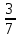
; 0)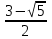
; 
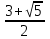
В решение входят целые числа: 1 и 2, сумма которых равна 3. Отв. 3.
8)
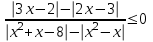
Заменим разности модулей разностями квадратов
, 
, 
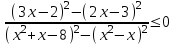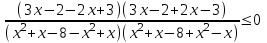
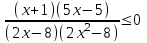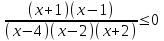
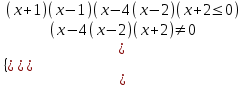
Решается методом интервалов
Отв. (-;-2)-1; 1(2; 4).
9)
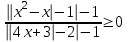
В силу рационализации: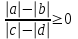
, 
, 
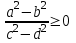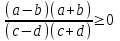, имеем
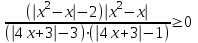. Используя то же преобразование, получим
, 
,
, 
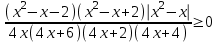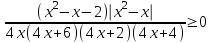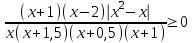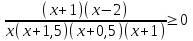
Решая методом интервалов, получим ответ
Отв. (-;-1,5)(-0,5; 0)12; ).
10)
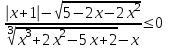
Применим тождество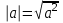
, 
, 
, 
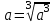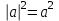
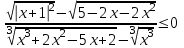
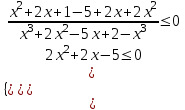
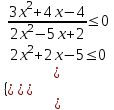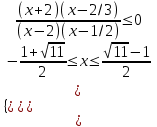
Используя метод интервалов, получим
Отв. -2; 1/2)2/3;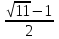
).
Показательные неравенства
1)
.
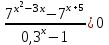В числителе левой части стоит разность значений возрастающей функции f(t) = 7t. В знаменателе разность значений убывающей функции g(t) = 0,3t, если представить 1 = 0,30. Применяя метод рационализации, получим
, 
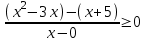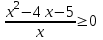. Применяя метод интервалов, получим ответ. Отв. -1; 0)5; ).
2)
.
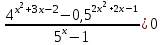Перейдем в числителе дроби к основанию 2, а в знаменателе – к основанию 5, и применим метод рационализации
, 
, 
, 
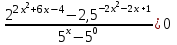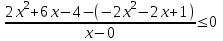
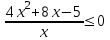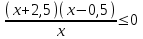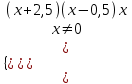
Применим метод интервалов
Отв. (-; -2,5(0; 0,5.
3)
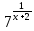
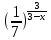
Применим метод рационализации
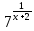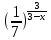- 0, (7 – 1)(
- 
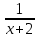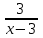) 0
(множитель (а – 1) = (7 – 1) автоматически учитывает характер монотонности показательной функции)
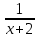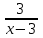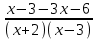( - ) 0,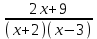 
0, 
0
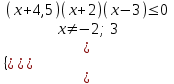. Отв. (-; -4,5(-2; 3).
4) 5x+2 + 5-x – 23 log464.
25∙5x + 5-x – 23 - log443 0, 25∙5x + 5-x – 26 0
t = 5x > 0, тогда
;
; 
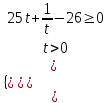
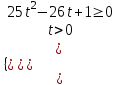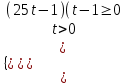
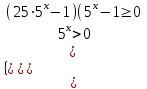, (5x+2 - 50)(5x – 50) 0, (5 - 1)(х + 2 - 0)(5 - 1)(х – 0) 0
(х + 2)х 0, х(-; -20; ).
5) 27x - 13∙9x + 13∙3x+1 – 27 0, t = 3x > 0, тогда
; 
; ; 
; 
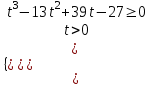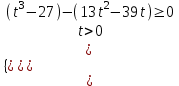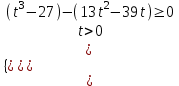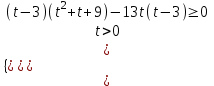
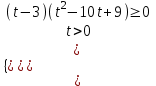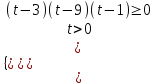; (3x - 3)(3x – 32)(3x – 30) 0.
Применяем метод рационализации
(3 - 1)(x - 1)(3 - 1)(x - 2)(3 - 1)(x - 0) 0, (x - 1)(x - 2)x 0
х0; 12; ).
6)
, 
, 
, 
, 
, 
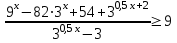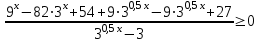
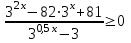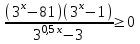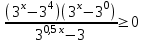
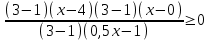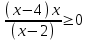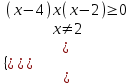
х0; 2)4; ).
7)
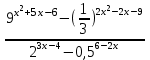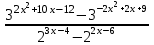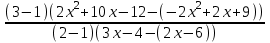0,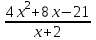 
0,
0, 
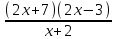0,
0,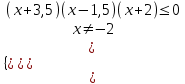 
х(-; -3,5(-2; 1,5.
8)
.
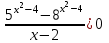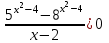, ОДЗ: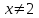 
Решим неравенство, используя метод рационализации
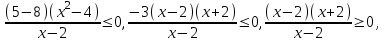
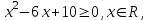
в)
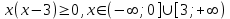
Решение исходного неравенства:
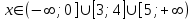
Ответ:
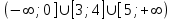
3)
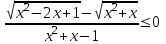.Заменим неравенство равносильной системой, используя метод рационализации
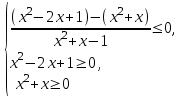
а)
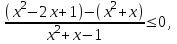
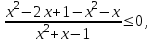
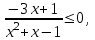
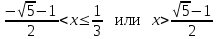
б)
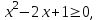
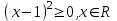
в)
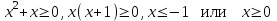
Решение исходного неравенства:
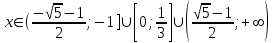
Ответ:
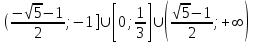
4)
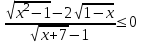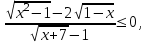
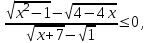
. Заменим неравенство равносильной системой, используя метод рационализации
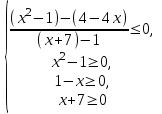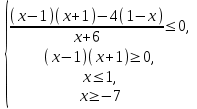
; а)
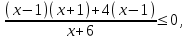
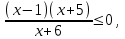
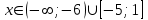
б)
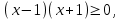
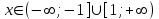
Решение исходного неравенства:
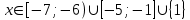. Ответ: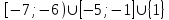 5)
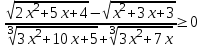.Т.к. 2x2 + 5x + 4 > 0 и x2 + 3x + 3 > 0 при всех х, то
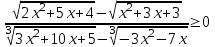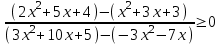
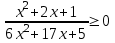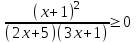
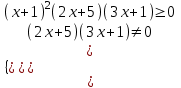
, , Отв. (-∞; -5/2)-1(-1/3; ∞).
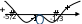
6) Найти сумму целых значений x, удовлетворяющих неравенству
(x + 3)
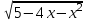0.Рассмотрим, сначала, уравнение
(x + 3)
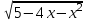= 0и найдем его корни:
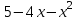= 0, x2 + 4x – 5 = 0, (x + 5)(x - 1) = 0, x1 = -5, x2 = 1.x + 3 = 0, x3 = -3
Отсюда, в частности, вытекает, что область определения исходного неравенства имеет вид x-5; 1.
Рассмотрим теперь строгое неравенство
(x + 3)
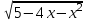< 0.В этом случае, в силу того, что квадратный корень положителен, выполняется неравенство
x + 3 < 0, x < -3,
откуда, воспользовавшись x-5; 1, получаем, что, решение исходного неравенства имеет вид:
x-5; -31
Для завершения решения задачи остается заметить, что в множество
-5; -31входят целые числа: -5, -4, -3, 1 , сумма которых равна -11.
Отв. -11.
7) Найти сумму всех целых чисел, являющихся решением неравенства
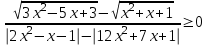.Т.к. 3x2 - 5x + 3 > 0 и x2 + x + 1 > 0 при всех х, то
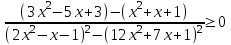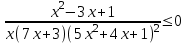, .Т.к. 5x2 + 4x + 1 > 0 при всех х, то
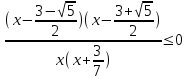x(-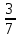
; 0)
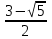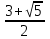
; В решение входят целые числа: 1 и 2, сумма которых равна 3. Отв. 3.
8)
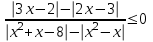
Заменим разности модулей разностями квадратов
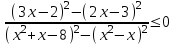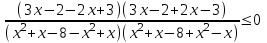
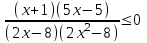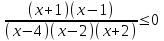
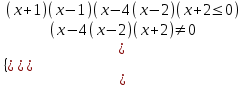
, , Решается методом интервалов
Отв. (-;-2)-1; 1(2; 4).
9)
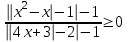
В силу рационализации:
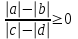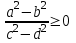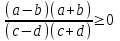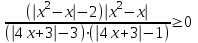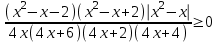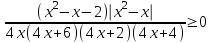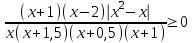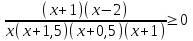
, , , имеем . Используя то же преобразование, получим , , , Решая методом интервалов, получим ответ
Отв. (-;-1,5)(-0,5; 0)12; ).
10)
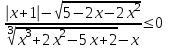
Применим тождество
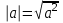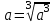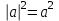
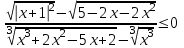
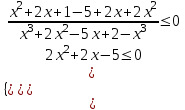
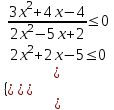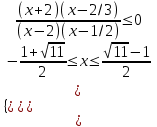
, , , Используя метод интервалов, получим
Отв. -2; 1/2)2/3;
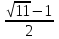).Показательные неравенства
| Выражение | Замена |
| af(x) – ag(x) | (a – 1)(f(x) – g(x)), (a > 0, a 1) |
| af(x) – b | (a – 1)(f(x) – logab), (a > 0, a 1), b > 0 |
| a(x)f(x) – 1 | (a(x) – 1)∙f(x), (a(x) > 0, a(x) 1) |
| a(x)f(x) – a(x)g(x) | (a(x) –1)(f(x) – g(x)), (a(x) > 0, a(x) 1) |
| a1(x)f(x) – a2(x)f(x) | (a1(x) – a2(x))∙f(x), (a1(x) > 0, a2(x) > 0) |
| f(x)h(x) – g(x)h(x) | (f(x) – g(x))∙h(x), (f(x) > 0, g(x) > 0) |
1)
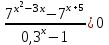.В числителе левой части стоит разность значений возрастающей функции f(t) = 7t. В знаменателе разность значений убывающей функции g(t) = 0,3t, если представить 1 = 0,30. Применяя метод рационализации, получим
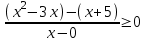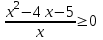, . Применяя метод интервалов, получим ответ. Отв. -1; 0)5; ).2)
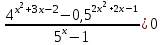.Перейдем в числителе дроби к основанию 2, а в знаменателе – к основанию 5, и применим метод рационализации
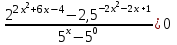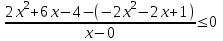
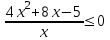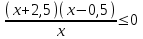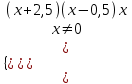
, , , Применим метод интервалов
Отв. (-; -2,5(0; 0,5.
3)
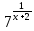
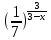
Применим метод рационализации
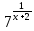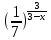- 0, (7 – 1)( 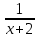- 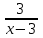) 0(множитель (а – 1) = (7 – 1) автоматически учитывает характер монотонности показательной функции)
(
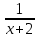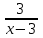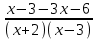- ) 0, 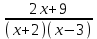0, 0 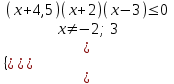. Отв. (-; -4,5(-2; 3).4) 5x+2 + 5-x – 23 log464.
25∙5x + 5-x – 23 - log443 0, 25∙5x + 5-x – 26 0
t = 5x > 0, тогда
;
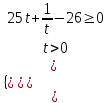
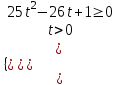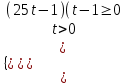
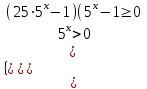; , (5x+2 - 50)(5x – 50) 0, (5 - 1)(х + 2 - 0)(5 - 1)(х – 0) 0(х + 2)х 0, х(-; -20; ).
5) 27x - 13∙9x + 13∙3x+1 – 27 0, t = 3x > 0, тогда
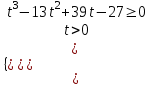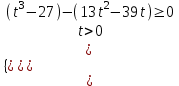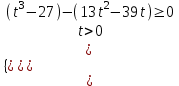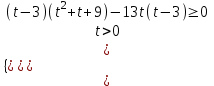
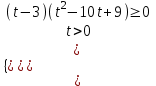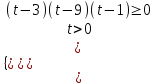; ; ; ; ; (3x - 3)(3x – 32)(3x – 30) 0.Применяем метод рационализации
(3 - 1)(x - 1)(3 - 1)(x - 2)(3 - 1)(x - 0) 0, (x - 1)(x - 2)x 0
х0; 12; ).
6)
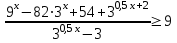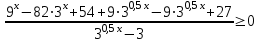
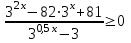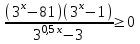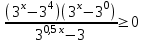
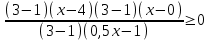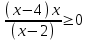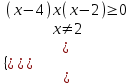
, , , , , х0; 2)4; ).
7)
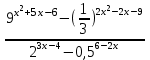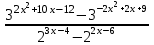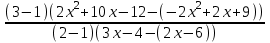0, 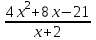0, 0,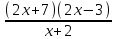 0, 0, 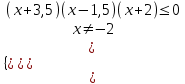х(-; -3,5(-2; 1,5.
8)
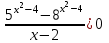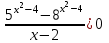. , ОДЗ: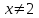 Решим неравенство, используя метод рационализации