Уметь составлять групповую и комбинационную таблицы!! Такая задача будет на экзамене!!!Задача: Проанализировать показатели процентного расхождения клинических и патологоанатомических диагнозов в БУ РКБ за 2015-2019 год.

год	2015	2016	2017	2018	2019
% расхождения диагнозов	8,2	9,6	9,1	8,9	9,0

1. 
   Абсолютный прирост или убыль ( из данных последующего года вычитаем предыдущий)
   

9,6-8,2=0,8; 9,1-9,6=-0,5; 8,9-9,1=-0,2; 9,0-8,9=0,1прирост это положительное число, убыль - отрицательное

2. 
   Темп прироста или убыли ( абсолютный прирост делим на данные предыдущего года)
   

0,8/8,2х100%=9,7%; -0,5/9,6х100%=-5,2%; -0,2/9,1х100%=-2,1%; 0,1/8,9х100%=1,1%

3. 
   Темп роста или убыли (данные последующего года делим на предыдущий и умножаем на 100%)
   

9,6/8,2х100%=117%; 9,1/9,6х100%=94%; 8,9/9,1х100%=97%; 9,0/8,9х100%=101%

4. 
   Абсолютное значение 1% прироста или убыли ( абсолютный прирост делим на темп прироста)
   

0,8/9,7=0,08; -0,5/-5,2=0,09; -0,2/-2,1=0,09; 0,1/1,1=0,094 показателя Анализа динамического ряда знать наизусть уметь рассчитывать. Будет такая задача на экзамене!!!1>1>1>1>1>1>1>1>1>1>1>1>1>1>1>1>1>1>

---

Тема 2: Средняя величина – это обобщающая характеристика, позволяющая оценить размер признака в совокупности, изменяющегося по своей величине.Средняя величина исчисляются для – характеристики уровень цен, заработной платы, основа капитала, численности населения.Требования к средней величине:

• 
  Средней величина должна характеризовать качественно однородную совокупность.
  
• 
  Ср. должны исчисляется по данным большого числа единиц, составляющих совокупность, то есть отображать массовые социально – экономические явления.
  

2 категории ср. величин:

• 
  Степенные средние
  
• 
  Структурные средние
  

Виды степенных ср. величин

1. 
   Арифметическая
   
2. 
   Геометрическая
   
3. 
   Гармоническая
   
4. 
   Квадратическая
   
5. 
   Кубическая
   

Расчет среднего возраста студентов в группе из 20 человек

№	Возраст
1	18
2	18
3	19
4	20
5	19
6	20
7	19
8	19
9	19
10	20
11	22
12	19
13	19
14	20
15	20
16	21
17	19
18	19
19	19
20	19

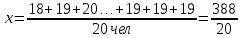=19,4 годаСтруктурные средние – особый вид средних величин, применяется для изучения внутреннего строения рядов, распределения значений признака, а так же для оценки средней величины (степенного типа) если по имеющимся статистическим данным ее расчет не может быть выполнен (например если бы в рассмотренном примере отсутствовали данные и об объеме производства и о сумме затрат по группе предприятий).

---

Для облегчения и ускорения подсчетов изучаемых признаков, их средних величин распределения, разнообразия, достоверности, результатов, а также достоверности их различия в сравниваемых группах используют методику вариационных рядов. Даже получая данные машинной обработки результатов, исследователь должен понимать, что они собой представляют.Вариационный ряд – ряд кол-ых значений изучаемого признака, построенного в возрастающем или убывающем порядке через отрытый интервал.Члены вариационного ряда:V –варианты, числовые значения признака;P – варианты, числовые значения признака;n – сумма всех частот (общее число всех вариант).Виды вариационных рядов:

1. 
   1.прерывные ≤ 1
   

2.непрерыыне – интервал > 1

2. 
   1. Простые (Несгруппированные) - которые составляются, как правило, при малом (до 30) числе наблюдений
   

2. Сгрупированные (которые составляются при большом (более 30) числе наблюдений)Основные требования к составлению вариационных рядов: 1. Расположить все варианты по порядку. 2. Суммировать единицы, имеющие одинаковый признак, т.е. найти частоту каждой варианты. 3. Определить число групп и размер интервала. 4. Разбить весь ряд на группы, используя выбранный интервал и строго соблюдая непрерывность сгруппированного ряда. 5. Дать графическое изображение.Малая выборка, это когда кол-во измерений n ≤ 30Средняя величина – наиболее типичная величина исследуемого признака в совокупности.Виды средних величин:

1. 
   Мода – Мо – величина, признак, который чаще всего встречается;
   
2. 
   Медиана – Ме – величина признака, занимающая срединное значение, или варианта, которая делит вар ряд пополам.
   

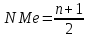
Если кол-во вариантов нечетноеЕсли число вариантов четное2 срединные варианты складываются и /2

3. 
   Средняя арифметическая – М
   

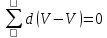
Свойство средней арифметической:1.занимает в вариационном ряду срединное значениеВ строго симметричном вар. ряду М=Мо-Ме2.среднее арифметическое носит абстрактный характер выражает наиболее типичное для всей совокупности3.сумма отклонений всех вариантов от средней = 0Виды средних арифметических:1.простая

---

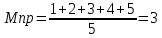
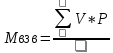
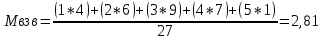
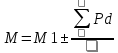
V P1-1 2-13-14-15-1n=52.Средняя арифметическая взвешенная V P1 4 2 63 94 75 13.Средняя арифметическая по способу моментов M1 – усл. средняя – Мо (мода)Р – частотаd – усл. отклонение от усл. среднейd=V-M1Какие величины характеризуют разнообразие признака в исследуемой совокупности 1)лимит – определяется крайними обозначениями в вар. 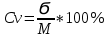ряду (Lim)2) амплитуда (Amp)- разность м/у крайними вар Amp= Vmax –Vmin3)ср.квадратичное отклонение (ϭ)4)коэффициент вариации (усл-СV)Если Сv >10, то разнообразие признака слабое.Если Сv от 10 до 20- среднее разнообразииЕсли Сv от 20 –сильное разнообразиеϬ- (среднее квадратное отклонение) характеризует разнообразие признаков учитывая внутреннюю структуру ряда (степень рассеянности или колеблемости признака)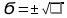Мпр= Ϭ 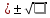, если n≤30, то (n-1)Мвзв= Ϭ 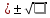, если n≤30, то (n-1)При расчете средней арифметической по способу математическомуϬ 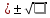m-ср ошибка средней арифметическойm= 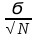Чем больше колеблется признак, тем> ϬЗадачи на нахождения средних величин н аэкзамене будет 2 типов, на нахождение М взвешенного ряда и по способу моментов. Чтобы вычислить столбик d надо из каждой варианты вычесть Мо( число которое находится посередине)В первом случае вы находите сначала Мвзвешанную по формуле 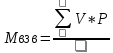, затем сигму по формуле Ϭ 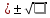, затем ошибку средней m, по формуле m=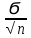

---

При расчете средней по способу моментов, вы находите М по сп.моментов, по формуле = , где М1 это Мода( срединное число), затем вы находите так же сигму, НО ПО ДРУГОЙ ФОРМУЛЕ Ϭ , и m - ошибка средней,по такой же формулеСредняя ошибка средней арифметической = m потому что мы исследуем не генеральную, а выборочную совокупность.m- Показывает насколько результаты, полученные при исследовании выборочной совокупности, отличались бы от исследования генеральной совокупности.t-критерий стьюдента, применяется для определения достоверности разности средней величины.t 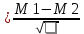1 гр.больных-лечили М-холиномиметиками2 гр.больных-М2 блокаторыСредняя арифметическая при рубцевании язвыМ1(1 гр)=30 дн m1=2,2М2(2 гр)=20 дн m2=1,5t=30-20/ √ 2,22 х 1,5 2= 6,25Такая задача будет на экзамене,уметь решать!Разность средней арифметической считается достоверной при +(критерии достоверности) ≥2Вывод: так как разность признака достоверна. То Н2 бл. Является эффективной в лечении ЯБ желудка.Тема 3: МКБ-10 введена ВОЗ в январе 1993 г переменно осевая классификация данные о болезнях сгруппированы следующим образом

1. 
   Эпидемиологические больные
   
2. 
   Конституциональные общие
   
3. 
   Местные болезни по анатомической локализации
   
4. 
   Болезни, связанные с развитием и травмы, выделяют 22 класса
   

Первый знак, когда –буква, каждая буква соответствует определенному классу, за исключением буквы «Д», которая используется в классе II «Новообразования» и в классе III «Болезни крови и кроветворных органов и определенные нарушения, вовлекающие иммунный механизм», буква «Н», которая используется в классе VII «Болезни глаза и придаточного аппарата» и в классе VIII «Болезни уха и сосцевидного отростка»4 класс – I, II, IIX, XX, - используют более 1 буквы в первом знаке своих кодов.Основы МКБ составляет единый кодовый перечень 3-х значных рубрик, каждая из которых далее может быть разделена на 4-х значные подрубрики числом до 10.Вместо числовой кодировки в предыдущих пересмотрах, в МКБ-10 использован буквенно-цифровой код с буквой в качестве первого знака и цифрой во 2, 3, 4 знаках кода.

---

Смотрите также файлы

• Презентация на тему Десмургия Подготовил Щербина Ю. Г. В качестве перевязочного материала используется.ppt

• Список использованных источников 47 Текстовая часть Задание пк 2, пк изучение особенностей компетенции учреждений социальной защиты населения. 1.docx

• Казанский государственный архитектурностроительный университет.docx

• Характеристика средств физического воспитания Оглавление.docx

• 1. Основные этапы организации партизанского движения на территории области. 1941 г.docx