Файл: Тема 1 Статистика. Организация и этапы статистического исследования.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 81
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
mr=

t=
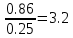
Задача: Дл/т=ср=М=ср=16
| Дл/тела | m | dx | dy | dx2 | dy2 | dxdy |
| 87 | 13 | -10 | -3 | 100 | 9 | 30 |
| 95 | 14 | -2 | -2 | 4 | 4 | 4 |
| 115 | 20 | +18 | +4 | 324 | 16 | 72 |
| 89 | 12 | -8 | -4 | 64 | 16 | 32 |
| 90 | 14 | -7 | -2 | 49 | 4 | 14 |
| 90 | 15 | -7 | -1 | 49 | 1 | 7 |
| 100 | 17 | 4 | +1 | 16 | 1 | 4 |
| 95 | 15 | -2 | -1 | 4 | 1 | 2 |
| 110 | 18 | +13 | +2 | 169 | 4 | 26 |
| 110 | 21 | +3 | +5 | 169 | 25 | 65 |
| 88 | 14 | -9 | -2 | 81 | 4 | 18 |
| 93 | 16 | -4 | 0 | 16 | 0 | 0 |
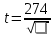
n=12
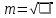 =0.12
=0.12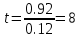
Тема 6: Корреляция признаков
Пятое свойство статистической совокупности - взаимосвязь (корреляция) признаков. В природе и обществе все процессы и явления взаимно связаны. Количественные связи проявляются в функциональной и корреляционной формах.
Функциональная связь: каждому значению одного признака соответствует строго определенное значение другого признака (характерна для физико-химических явлений). Корреляционная связь: каждому значению одного признака соответствует несколько значений другого признака (характерна для социально-гигиенических и медикобиологических процессов).
Корреляционная связь проявляется лишь при массовом сопоставлении признаков в качественно однородной совокупности.
Признаки могут быть качественными и количественными несгруппированными величинами (абсолютными и производными). Задача специалиста - найти причинные связи, подтверждающие зависимость одного явления от другого или от какой-то общей причины.
Корреляция может быть представлена в виде таблиц, графика или коэффициента корреляции.
Коэффициент корреляции (r,p) дает представление о направлении (прямая +, обратная -) и силе связи (от 0 до 1):
0 - связь отсутствует;
0-0,3 - связь слабая;
0,3-0,7 - связь средняя;
0,7-1,0 - связь сильная.
Обычный, наиболее точный и часто применяемый метод (коэффициент) Пирсона:

Более грубый, приближенный и простой ранговый метод Спирмена:

Задача: Определите методом корреляции рангов направление и силу связи если даны следующие данные роста и массы 7 летних детей:
| N-число наблюдений | Рост исследуемых в см, Х | Масса исследуемых в кг, Y | Порядковые номера(ранги) признаков | Разность рангов (х-у)=d | Квадрат разности рангов, d 2 | ||
| Х | Y | ||||||
| 1 | 87 | 13 | 1 | 2 | -1 | 1 | |
| 2 | 95 | 14 | 7,5 | 4 | 3,5 | 12,25 | |
| 3 | 115 | 20 | 12 | 11 | 1 | 1 | |
| 4 | 89 | 12 | 3 | 1 | 2 | 4 | |
| 5 | 90 | 14 | 4,5 | 4 | 0,5 | 0,25 | |
| 6 | 90 | 15 | 4,5 | 6,5 | -2 | 4 | |
| 7 | 101 | 17 | 9 | 9 | 0 | 0 | |
| 8 | 95 | 15 | 7,5 | 6,5 | 1 | 1 | |
| 9 | 110 | 18 | 10,5 | 10 | 0,5 | 0,25 | |
| 10 | 110 | 21 | 10,5 | 12 | 1,5 | 2,25 | |
| 11 | 88 | 14 | 2 | 4 | -2 | 4 | |
| 12 | 93 | 16 | 6 | 8 | -2 | 4 | |
Ранги-это порядковые номера, он присваивается в порядке возрастания, если число повторяется ранги присваиваются по порядку, складываются и делятся на количество измерений. Например в нашей задаче мы начинаем присваивать ранги с минимального значения, так для числа 87 присваивается ранг 1,для 88-2,89-3, дальше число 90 повторяется 2 раза, мы присваиваем ему ранг 4 и 5, складываем их и делим на 2,т.к. число 90 встречается 2 раза, и т.д.
p= 1-
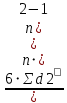 ; mp=
; mp= ; t=
; t=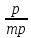 ;
;Подставляем числа в формулы и находим t, делаем оценку силы и направления связи. В данном случае t = 3.6 - связь прямая,сильная,достоверная.
Такая задача тоже будет на экзамене и тоже нужно уметь решать!!!