Файл: Исследовательская работа Аналогии в математике Автор Андреев Егор моу Зашижемская сош Сидоркина Р. Л.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 42
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МОУ «Зашижемская средняя общеобразовательная школа»
Исследовательская работа
Аналогии в математике
Автор:
Андреев Егор
МОУ «Зашижемская СОШ»
Руководитель:
Сидоркина Р.Л.,
учитель математики высшей
категории
МОУ «Зашижемская СОШ»
Зашижемье,
2019
Содержание
-
Введение………………………………………………………………………… 2
-
Глава 1.Теоретико-методический аспект геометрических аналогий……… 6
-
Структурно-функциональный анализ треугольника и тетраэдра………… 6
1.2 Эмпирические исследования треугольника и тетраэдра…………………… 9
3. Глава 2. Фольклор и математика……………………………………………… 11
4. Глава 3. Математика и поэзия………………………………………………… 14
5. Глава 4. Математика в песенном творчестве………………………………… 17
Заключение…………………………………………………………………………… 19
Литература…………………………………………………………………………… 21
Приложение ………………………………………………………………………… 22
Введение
…Я больше всего дорожу аналогиями,
моими верными учителями .Они знают
все секреты природы, и ими меньше все
го следует пренебрегать.
Ян Кеплер
В 90 – е годы прошлого века начали говорить о необходимости сочетать серьезное естественно-научное и техническое образование с гуманитарным. Сейчас все большую популярность завоевывает такая, на первый взгляд, парадоксальная идея: лучшее усвоение знаковой информации, которую несет математика, происходит при помощи лучшего усвоения образной информации – музыки, поэзии, фольклора, живописи.
Избежать односторонности в изучении математики может помочь широкое применение метода аналогии.
Аналогия – есть некоторого рода сходство, но на более определенном и выраженном с помощью понятий уровне. Различие между аналогией и другими видами сходства заключается в намерениях думающего. Сходные предметы согласуются между собой в каком-то отношении, и если свести это отношение, в котором они согласуются, к определенным понятиям, то можно рассмотреть эти сходные предметы как аналогичные. Если удается добраться до ясных понятий, то выясняется аналогия.
Аналогия (греч. analogia – соответствие, сходство), сходство предметов (явлений, процессов) в каких-либо свойствах.
Аналогии могут быть двух видов:
-
Простая аналогия, при которой по сходству объектов в некоторых признаках заключают их сходство в других признаках.
-
Распространенная аналогия, при которой из сходства явлений делают вывод о сходстве причин.
В свою очередь, простая и распространенная аналогии могут быть:
а) строгой аналогией, при которой признаки сравниваемых объектов находятся во взаимной зависимости;
б) нестрогой аналогией, при которой признаки сравниваемых объектов не находятся в явной взаимной зависимости.
Строгая аналогия применяется в научных исследованиях, в математических доказательствах, а при решении задач (арифметических, геометрических и др.) используется либо алгоритм, либо нестрогая аналогия с уже решенными однотипными задачами.
Аналогия является, пожалуй, одним из самых распространенных методов научного исследования. Широкое применение аналогий часто приводит исследователя к более или менее правдоподобным предположениям о свойствах изучаемого объекта, которые затем могут подтверждены или опровергнуты опытом или более строгими рассуждениями.
Например, некоторые свойства треугольника и тетраэдра похожи, а многие геометрические понятия, связанные с треугольником, имеют пространственные аналогии. Мы знаем, что геометрия делится на два основных раздела: планиметрия (фигуры на плоскости) и стереометрия (фигуры в пространстве) Например:
-Сторона треугольника – грань тетраэдра;
-длина стороны – площадь грани;
-вписанная окружность – вписанная сфера;
-описанная окружность – описанная сфера; площадь – объем
-Каждая сторона прямоугольника параллельна и равна одной другой
стороне и перпендикулярна остальным -
каждая грань прямоугольного параллелепипеда параллельна и равна
одной другой грани и перпендикулярна остальным;
-В равнобедренном треугольнике углы при основании равны -
- углы при каждом основании равнобедренной трапеции равны.
и т. д.
Эта аналогия не только внешняя. Многие теоремы о треугольниках, если применить в их формулировках планиметрические термины, соответствующие стереометрическим, и соответствующим образом «подправить» формулировки, превращаются в теоремы о тетраэдрах. Несколько таких теорем и задач рассмотрим в данной работе.
Кроме установления аналогий между математическими понятиями, мы в своей работе проследим математико-гуманитарные аналогии. Попытаемся перевести математику, ее правила, методы, проблемы, задачи, теоремы на язык гуманитарной культуры, на язык образов, символов и эмоций. Именно такими методами иногда педагоги стараются довести до нас некоторые термины и понятия из геометрии и алгебры. В качестве исследования рассмотрим литературные произведения (загадки, песни, стихотворения и пр.) сквозь призму математических знаний, попытаемся найти то, что объединяет их с математикой (установить ассоциацию по схожести), интерпретировать математику языком литературы.
Цель исследования – рассмотреть геометрические и математико-гуманитарные аналогии.
Задачи исследования:
-
Изучить учебную, методическую, энциклопедическую литературу.
-
Определить сущность аналогии и ее виды.
-
Выделить признаки сравниваемых объектов, находящихся во взаимной зависимости, через доказательство теорем и решение задач.
-
Установить аналогии между математическими и литературными объектами.
-
Привести примеры парных задач на плоскости и в пространстве.
Объект исследования – геометрические аналогии в учебниках геометрии 9 и 10 – 11 классов на примере треугольника и тетраэдра; некоторые образцы литературного и песенного творчества.
Предмет исследования – треугольник и тетраэдр, фольклор и математика, математика и поэзия, математика и песня.
Методы исследования: анализ учебной, методической, энциклопедической, научно-популярной литературы; сравнительный анализ, выявление аналогий
Рассмотрев понятие «аналогия», мы выявили для себя гипотезы:
1)между тетраэдром и треугольником существуют аналогии;
2) между фольклором и математикой существуют аналогии;
3) между математикой и поэзией существуют аналогии;
4) между математикой и песней существуют аналогии;
В результате своего исследования мы постараемся подтвердить либо опровергнуть данные гипотезы.
Глава 1. Теоретико-методический аспект геометрических аналогий
1.1 Структурно-функциональный анализ треугольника и тетраэдра
МОУ «Зашижемская средняя общеобразовательная школа»
Исследовательская работа
Аналогии в математике
Автор:
Андреев Егор
МОУ «Зашижемская СОШ»
Руководитель:
Сидоркина Р.Л.,
учитель математики высшей
категории
МОУ «Зашижемская СОШ»
Зашижемье,
2019
Содержание
-
Введение………………………………………………………………………… 2
-
Глава 1.Теоретико-методический аспект геометрических аналогий……… 6
-
Структурно-функциональный анализ треугольника и тетраэдра………… 6
1.2 Эмпирические исследования треугольника и тетраэдра…………………… 9
3. Глава 2. Фольклор и математика……………………………………………… 11
4. Глава 3. Математика и поэзия………………………………………………… 14
5. Глава 4. Математика в песенном творчестве………………………………… 17
Заключение…………………………………………………………………………… 19
Литература…………………………………………………………………………… 21
Приложение ………………………………………………………………………… 22
Введение
…Я больше всего дорожу аналогиями,
моими верными учителями .Они знают
все секреты природы, и ими меньше все
го следует пренебрегать.
Ян Кеплер
В 90 – е годы прошлого века начали говорить о необходимости сочетать серьезное естественно-научное и техническое образование с гуманитарным. Сейчас все большую популярность завоевывает такая, на первый взгляд, парадоксальная идея: лучшее усвоение знаковой информации, которую несет математика, происходит при помощи лучшего усвоения образной информации – музыки, поэзии, фольклора, живописи.
Избежать односторонности в изучении математики может помочь широкое применение метода аналогии.
Аналогия – есть некоторого рода сходство, но на более определенном и выраженном с помощью понятий уровне. Различие между аналогией и другими видами сходства заключается в намерениях думающего. Сходные предметы согласуются между собой в каком-то отношении, и если свести это отношение, в котором они согласуются, к определенным понятиям, то можно рассмотреть эти сходные предметы как аналогичные. Если удается добраться до ясных понятий, то выясняется аналогия.
Аналогия (греч. analogia – соответствие, сходство), сходство предметов (явлений, процессов) в каких-либо свойствах.
Аналогии могут быть двух видов:
-
Простая аналогия, при которой по сходству объектов в некоторых признаках заключают их сходство в других признаках.
-
Распространенная аналогия, при которой из сходства явлений делают вывод о сходстве причин.
В свою очередь, простая и распространенная аналогии могут быть:
а) строгой аналогией, при которой признаки сравниваемых объектов находятся во взаимной зависимости;
б) нестрогой аналогией, при которой признаки сравниваемых объектов не находятся в явной взаимной зависимости.
Строгая аналогия применяется в научных исследованиях, в математических доказательствах, а при решении задач (арифметических, геометрических и др.) используется либо алгоритм, либо нестрогая аналогия с уже решенными однотипными задачами.
Аналогия является, пожалуй, одним из самых распространенных методов научного исследования. Широкое применение аналогий часто приводит исследователя к более или менее правдоподобным предположениям о свойствах изучаемого объекта, которые затем могут подтверждены или опровергнуты опытом или более строгими рассуждениями.
Например, некоторые свойства треугольника и тетраэдра похожи, а многие геометрические понятия, связанные с треугольником, имеют пространственные аналогии. Мы знаем, что геометрия делится на два основных раздела: планиметрия (фигуры на плоскости) и стереометрия (фигуры в пространстве) Например:
-Сторона треугольника – грань тетраэдра;
-длина стороны – площадь грани;
-вписанная окружность – вписанная сфера;
-описанная окружность – описанная сфера; площадь – объем
-Каждая сторона прямоугольника параллельна и равна одной другой
стороне и перпендикулярна остальным -
каждая грань прямоугольного параллелепипеда параллельна и равна
одной другой грани и перпендикулярна остальным;
-В равнобедренном треугольнике углы при основании равны -
- углы при каждом основании равнобедренной трапеции равны.
и т. д.
Эта аналогия не только внешняя. Многие теоремы о треугольниках, если применить в их формулировках планиметрические термины, соответствующие стереометрическим, и соответствующим образом «подправить» формулировки, превращаются в теоремы о тетраэдрах. Несколько таких теорем и задач рассмотрим в данной работе.
Кроме установления аналогий между математическими понятиями, мы в своей работе проследим математико-гуманитарные аналогии. Попытаемся перевести математику, ее правила, методы, проблемы, задачи, теоремы на язык гуманитарной культуры, на язык образов, символов и эмоций. Именно такими методами иногда педагоги стараются довести до нас некоторые термины и понятия из геометрии и алгебры. В качестве исследования рассмотрим литературные произведения (загадки, песни, стихотворения и пр.) сквозь призму математических знаний, попытаемся найти то, что объединяет их с математикой (установить ассоциацию по схожести), интерпретировать математику языком литературы.
Цель исследования – рассмотреть геометрические и математико-гуманитарные аналогии.
Задачи исследования:
-
Изучить учебную, методическую, энциклопедическую литературу.
-
Определить сущность аналогии и ее виды.
-
Выделить признаки сравниваемых объектов, находящихся во взаимной зависимости, через доказательство теорем и решение задач.
-
Установить аналогии между математическими и литературными объектами.
-
Привести примеры парных задач на плоскости и в пространстве.
Объект исследования – геометрические аналогии в учебниках геометрии 9 и 10 – 11 классов на примере треугольника и тетраэдра; некоторые образцы литературного и песенного творчества.
Предмет исследования – треугольник и тетраэдр, фольклор и математика, математика и поэзия, математика и песня.
Методы исследования: анализ учебной, методической, энциклопедической, научно-популярной литературы; сравнительный анализ, выявление аналогий
Рассмотрев понятие «аналогия», мы выявили для себя гипотезы:
1)между тетраэдром и треугольником существуют аналогии;
2) между фольклором и математикой существуют аналогии;
3) между математикой и поэзией существуют аналогии;
4) между математикой и песней существуют аналогии;
В результате своего исследования мы постараемся подтвердить либо опровергнуть данные гипотезы.
Глава 1. Теоретико-методический аспект геометрических аналогий
1.1 Структурно-функциональный анализ треугольника и тетраэдра
МОУ «Зашижемская средняя общеобразовательная школа»
Исследовательская работа
Аналогии в математике
Автор:
Андреев Егор
МОУ «Зашижемская СОШ»
Руководитель:
Сидоркина Р.Л.,
учитель математики высшей
категории
МОУ «Зашижемская СОШ»
Зашижемье,
2019
Содержание
-
Введение………………………………………………………………………… 2 -
Глава 1.Теоретико-методический аспект геометрических аналогий……… 6
-
Структурно-функциональный анализ треугольника и тетраэдра………… 6
1.2 Эмпирические исследования треугольника и тетраэдра…………………… 9
3. Глава 2. Фольклор и математика……………………………………………… 11
4. Глава 3. Математика и поэзия………………………………………………… 14
5. Глава 4. Математика в песенном творчестве………………………………… 17
Заключение…………………………………………………………………………… 19
Литература…………………………………………………………………………… 21
Приложение ………………………………………………………………………… 22
Введение
…Я больше всего дорожу аналогиями,
моими верными учителями .Они знают
все секреты природы, и ими меньше все
го следует пренебрегать.
Ян Кеплер
В 90 – е годы прошлого века начали говорить о необходимости сочетать серьезное естественно-научное и техническое образование с гуманитарным. Сейчас все большую популярность завоевывает такая, на первый взгляд, парадоксальная идея: лучшее усвоение знаковой информации, которую несет математика, происходит при помощи лучшего усвоения образной информации – музыки, поэзии, фольклора, живописи.
Избежать односторонности в изучении математики может помочь широкое применение метода аналогии.
Аналогия – есть некоторого рода сходство, но на более определенном и выраженном с помощью понятий уровне. Различие между аналогией и другими видами сходства заключается в намерениях думающего. Сходные предметы согласуются между собой в каком-то отношении, и если свести это отношение, в котором они согласуются, к определенным понятиям, то можно рассмотреть эти сходные предметы как аналогичные. Если удается добраться до ясных понятий, то выясняется аналогия.
Аналогия (греч. analogia – соответствие, сходство), сходство предметов (явлений, процессов) в каких-либо свойствах.
Аналогии могут быть двух видов:
-
Простая аналогия, при которой по сходству объектов в некоторых признаках заключают их сходство в других признаках. -
Распространенная аналогия, при которой из сходства явлений делают вывод о сходстве причин.
В свою очередь, простая и распространенная аналогии могут быть:
а) строгой аналогией, при которой признаки сравниваемых объектов находятся во взаимной зависимости;
б) нестрогой аналогией, при которой признаки сравниваемых объектов не находятся в явной взаимной зависимости.
Строгая аналогия применяется в научных исследованиях, в математических доказательствах, а при решении задач (арифметических, геометрических и др.) используется либо алгоритм, либо нестрогая аналогия с уже решенными однотипными задачами.
Аналогия является, пожалуй, одним из самых распространенных методов научного исследования. Широкое применение аналогий часто приводит исследователя к более или менее правдоподобным предположениям о свойствах изучаемого объекта, которые затем могут подтверждены или опровергнуты опытом или более строгими рассуждениями.
Например, некоторые свойства треугольника и тетраэдра похожи, а многие геометрические понятия, связанные с треугольником, имеют пространственные аналогии. Мы знаем, что геометрия делится на два основных раздела: планиметрия (фигуры на плоскости) и стереометрия (фигуры в пространстве) Например:
-Сторона треугольника – грань тетраэдра;
-длина стороны – площадь грани;
-вписанная окружность – вписанная сфера;
-описанная окружность – описанная сфера; площадь – объем
-Каждая сторона прямоугольника параллельна и равна одной другой
стороне и перпендикулярна остальным -
каждая грань прямоугольного параллелепипеда параллельна и равна
одной другой грани и перпендикулярна остальным;
-В равнобедренном треугольнике углы при основании равны -
- углы при каждом основании равнобедренной трапеции равны.
и т. д.
Эта аналогия не только внешняя. Многие теоремы о треугольниках, если применить в их формулировках планиметрические термины, соответствующие стереометрическим, и соответствующим образом «подправить» формулировки, превращаются в теоремы о тетраэдрах. Несколько таких теорем и задач рассмотрим в данной работе.
Кроме установления аналогий между математическими понятиями, мы в своей работе проследим математико-гуманитарные аналогии. Попытаемся перевести математику, ее правила, методы, проблемы, задачи, теоремы на язык гуманитарной культуры, на язык образов, символов и эмоций. Именно такими методами иногда педагоги стараются довести до нас некоторые термины и понятия из геометрии и алгебры. В качестве исследования рассмотрим литературные произведения (загадки, песни, стихотворения и пр.) сквозь призму математических знаний, попытаемся найти то, что объединяет их с математикой (установить ассоциацию по схожести), интерпретировать математику языком литературы.
Цель исследования – рассмотреть геометрические и математико-гуманитарные аналогии.
Задачи исследования:
-
Изучить учебную, методическую, энциклопедическую литературу. -
Определить сущность аналогии и ее виды. -
Выделить признаки сравниваемых объектов, находящихся во взаимной зависимости, через доказательство теорем и решение задач. -
Установить аналогии между математическими и литературными объектами. -
Привести примеры парных задач на плоскости и в пространстве.
Объект исследования – геометрические аналогии в учебниках геометрии 9 и 10 – 11 классов на примере треугольника и тетраэдра; некоторые образцы литературного и песенного творчества.
Предмет исследования – треугольник и тетраэдр, фольклор и математика, математика и поэзия, математика и песня.
Методы исследования: анализ учебной, методической, энциклопедической, научно-популярной литературы; сравнительный анализ, выявление аналогий
Рассмотрев понятие «аналогия», мы выявили для себя гипотезы:
1)между тетраэдром и треугольником существуют аналогии;
2) между фольклором и математикой существуют аналогии;
3) между математикой и поэзией существуют аналогии;
4) между математикой и песней существуют аналогии;
В результате своего исследования мы постараемся подтвердить либо опровергнуть данные гипотезы.
Глава 1. Теоретико-методический аспект геометрических аналогий
1.1 Структурно-функциональный анализ треугольника и тетраэдра
| Отметим какие-нибудь три точки А,В,С, не лежащие на одной прямой, и соединим их отрезками АВ, ВС, АС (рис.1). 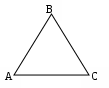 Рис. 1 Мы получили геометрическую фигуру, которая называется треугольником. Точки А, В, С называются вершинами, отрезки АВ, ВС, АС – сторонами, три угла    ВАС, САВ, АСВ – углами треугольника. Название «треугольник» происходит от греческого слова тригонон. ВАС, САВ, АСВ – углами треугольника. Название «треугольник» происходит от греческого слова тригонон. | Р 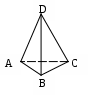 ассмотрим произвольный треугольник АВС и точку D, не лежащую в плоскости этого треугольника. Соединив точку D с вершинами треугольника АВС, получим треугольники DAB, DBC и DCA. Поверхность, составленная из четырех треугольников АВС, DAB, DBC и DCA называется тетраэдром и обозначается так: DABC (рис.2). ассмотрим произвольный треугольник АВС и точку D, не лежащую в плоскости этого треугольника. Соединив точку D с вершинами треугольника АВС, получим треугольники DAB, DBC и DCA. Поверхность, составленная из четырех треугольников АВС, DAB, DBC и DCA называется тетраэдром и обозначается так: DABC (рис.2).Рис. 2 Треугольники из которых состоит тетраэдр, называются гранями, их стороны – ребрами, а вершины – вершинами тетраэдра. Тетраэдр имеет четыре грани, шесть ребер и четыре вершины. Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. На рис.2 противоположными являются ребра AD и ВС, DB и АС, DC и АВ. Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие – боковыми гранями. Название «тетраэдр» происходит от греческого слова tetra (тетра) – «четыре» и греческого слова edra (эдра) – «основание». |
Виды треугольников и тетраэдров
Правильный треугольник – правильный тетраэдр;
Равнобедренный треугольник – правильная треугольная пирамида;
Равносторонний треугольник – тетраэдр общего вида;
Прямоугольный треугольник – тетраэдр, в котором все три плоских угла при одной вершине прямые.
Важно отметить следующий факт: не все свойства треугольника имеют аналогии среди свойств тетраэдра. Например, все высоты любого треугольника пересекаются в одной точке, но не о каждом тетраэдре можно сказать тоже самое.
Те тетраэдры, для которых такое свойство верно, составляют класс ортоцентрических тетраэдров.
Признаки равенства треугольников и тетраэдров
Признаки равенства треугольников – одна из тем, которая остается актуальной на протяжении всего курса планиметрии. В стереометрии признаки равенства тетраэдров не рассматриваются.
Равенство треугольников и тетраэдров определяются на основе понятия наложения:
| Два треугольника называются равными, если их можно совместить наложением. | Две пирамиды называются равными, если они при вложении одной в другую могут быть совмещены. |
Для доказательства признаков равенства тетраэдров необходимо знать признаки равенства трехгранных углов, а именно:
● Два трехгранных угла равны, если все три плоские угла одного из них равны плоским углам другого и одинаково с ними расположены;
● Два трехгранных угла равны, если они имеют по равному трехгранному углу, заключенному между двумя двухгранными углами, соответственно равными и одинаково расположенными;
● Два трехгранных угла равны, если они имеют по равному плоскому углу, заключенному между двумя двухгранными углами, соответственно равными и одинаково расположенными.
| | Признаки равенства треугольников | Признаки равенства тетраэдров |
| I | Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. | Если в двух тетраэдрах соответственно равны две грани и двугранный угол между ними, то такие тетраэдры равны или симметричны. |
| II | Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. | Два тетраэдра равны или симметричны, если они имеют по равному ребру, прилежащему к соответственно равным трехгранным углам. |
| III | Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Признаки равенства треугольников (Приложение №1) | Два тетраэдра равны или симметричны, если они имеют по шесть равных ребер, и в обоих тетраэдрах равные элементы располагаются в одном и том же порядке (так, что трем ребрам, лежащим в одной грани или выходящим из одной вершины, соответствуют три равных им ребра, также лежащие в одной грани или выходящие из одной вершины). |
Поясним понятие «симметричные тетраэдры».
● Если ребра, плоские и двугранные углы двух тетраэдров равны, но расположены в «обратном» порядке, то они симметричны.
На рис. 3 изображен тетраэдр ОАВС. Его ребра АО, СО, ВО продолжены за вершину О так, что АО=ОА1, СО=ОС1, ВО=ОВ1.
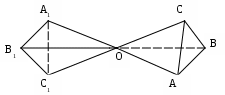
Рис. 3
В тетраэдрах ОАВС и ОА1В1С1 равны ребра, плоские и двугранные углы, следовательно, они симметричны.
Заметим, что симметричные тетраэдры, вообще говоря, не равны, то есть при вложении одного тетраэдра в другой они не совмещаются.
1.2 Эмпирические исследования треугольника и тетраэдра
| | Теоремы о замечательных точках треугольника | Стереометрические аналогии теорем о замечательных точках треугольника |
| I | Биссектрисы треугольника пересекаются в одной точке, которая удалена от сторон углов треугольника на одинаковое расстояние. Приложение №2 | Биссекторные (Приложение №3) плоскости двугранных углов трехгранного угла пересекаются по одной прямой, и каждая точка этой прямой удалена от граней трехгранного угла на одно и то же расстояние. |
| II | Медианы треугольника пересекаются в одной точке. Приложение №4 | Плоскости, проходящие через биссектрисы плоских углов каждой грани трехгранного угла и противолежащего им ребра, пересекаются по одной прямой. |
| III | Высоты треугольника или их продолжения пересекаются в одной точке. Приложение №5 | Плоскости, проходящие через ребра трехгранного угла перпендикулярно к противолежащей грани, пересекаются по одной прямой. |
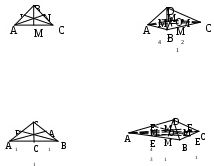
| ● Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. | ● Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется медианой тетраэдра. |
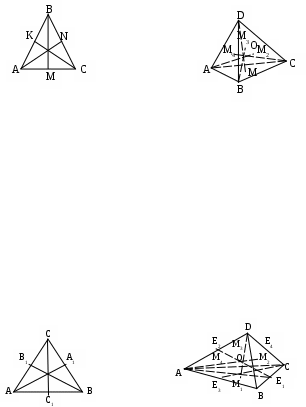  Отрезки ВМ, СК, АН – медианы треугольника | Точки М1, М2, М3, М4 -точки пересечения медиан граней. Отрезки АМ2, DM1, BM3, СМ4 – медианы тетраэдра |
| Свойство медиан треугольника [1, с. 67] Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершин. Доказательство: 1. Рассмотрим произвольный ∆АВС. МедианыАА1,ВВ1,СС1пересекаются в точке О. 2. В1А1 – средняя линяя треугольника. В1А1║АВ, <1=<2,<3=<4. ∆АОВ∆A1OB1 (по двум углам) 3. АО = 2А1О, ВО + 2В1О. | Свойство медиан тетраэдра [3, с. 23] Четыре медианы тетраэдра пересекаются в одной точке и делятся ею в отношении 3:1, считая от вершин. Доказательство:
Отрезки DM1 и АМ2 пересекаются в точке О.
∆AE1D ∆M1E1M2, значит,
|
| 4. Аналогично доказывается, что точка пересечения медиан ВВ1 и СС1 делит каждую из них в отношении 2 : 1, считая от вершины, и, следовательно совпадает с точкой О. Все три медианы ∆АВС пересекаются в точке О и делятся ею в отношении 2 : 1, считая от вершины | 4. Повторив рассуждения для ∆ВЕ5D и ∆СЕ3D, получим, что отрезок ВM3 и CM4 пересекают отрезок DM1 в точке, делящей его в отношении 3 : 1, считая от вершины, то есть в точке О. ВM3 : CM4 = 3 : 1. |
Мы рассмотрели теоремы о замечательных точках треугольника, и нашли аналогичные им для тетраэдра. Данные свойства медиан, биссектрис и высот необходимы при доказательстве более сложных теорем и решения сложных задач.
Мы решили провести целенаправленную работу по установлению аналогий, выбрав в качестве поля их поиска разнообразные литературные произведения всевозможных жанров, включая фольклорные.
Глава 2.Фольклорные метафоры математики
Установление различных видов зависимостей можно рассматривать на фольклорном материале. За фольклорным объектом может угадываться и математический объект.
В таблице установлены фольклорные аналогии и соответствующие им математические объекты.
| Математический объект | Фольклорный объект | Примечание |
| Аксиома | Ясно, как дважды два | |
| Метод от противного | Не было бы счастья, да несчастье помогло | |
| Параллельные плоскости | Загадка: два быка бодаются, вместе не сойдутся | Отгадка: небо и земля |
| Параллельные прямые | Загадка: два братца в воду глядятся, век не сойдутся | Отгадка: берега реки |
| Отрезок | Было бы начало, будет и конец. Как бечевку ни вить, а концу быть. Ласточка весну начинает, а соловей кончает | |
| Прямая | Загадка: шагаешь – впереди лежит, оглянешься – назад бежит. Будешь ты у меня по ниточке ходить. | Отгадка: дорога |
| Круг и шар | Загадка: без окон, без дверей, полна горница людей. | Здесь аналогия составлена не по отгадке, а по тому признаку, что круг и шар –фигуры ,полностью «заполненные» точками |
| Через две точки можно провести только одну прямую | На двух якорях корабль крепче держится | Две точки задают прямую, однозначно ,закрепляют ее местоположение так же, как якоря – положение корабля |
| Прямая, перпендикулярная плоскости | Загадка: сто один брат, все в один ряд, вместе связаны стоят | Отгадка: забор. Каждый «брат» перпендикулярен земле |
| Проекция наклонной | От своей тени не убежишь. Загадка: сколько по ней ни иди, всё будет бежать впереди. | Отгадка: тень Всякая наклонная имеет проекцию, как всякий предмет – тень |
| Перпендикуляр из точки на прямую | С одного вола двух шкур не дерут (словацкая мудрость) | Из одной точки к прямой двух перпендикуляров не провести |
| Нулевой вектор | У нашего господина нет ни ржи, ни овина | Все координаты равны нулю |
| Квадрат | Что вдоль, что поперек | |
| Луч | Загадка: придет в дом, не выгонишь колом, пора придет – сам уйдет | Отгадка: солнечный луч |
| Немонотонная функция | Не всё в гору, ино и под гору | |
| Возрастающая функция (прямая пропорциональность) | Чем дальше в лес, тем больше дров. Дальше в спор – больше слов. Больше почет – больше хлопот. Много снега – много хлеба. Меньше конь – меньше воз. Много гостей – много и новостей. Как аукнется – так и откликнется. | |
| Убывающая функция (обратная пропорциональность) | Тише едешь – дальше будешь. Высоко летаешь – низко упадешь. Дальше от кузницы -меньше копоти. Дальше положишь – ближе возьмешь. Меньше лести – больше чести. Меньше знаешь – крепче спишь | |
| График постоянной функции | Ни под гору, ни в гору | |
| Синусоида (косинусоида) | Загадка: По морю идет, а как на берег выползет, тут и пропадает | Отгадка: волна (форма графика) |
| Парабола | Загадка: Разноцветное коромысло над рекою повисло | Отгадка: радуга (имеет форму параболы с ветвями, направленными вниз) |
| Симметрия | Загадка: Перед нами вверх ногами, перед тобой –вверх головой | Отгадка: отражение в воде |
| Куб | Загадка: От воды родится, а воды боится | Отгадка: соль. кристаллы соли имеют форму куба |
| Посторонний корень | Пятое колесо в телеге. Сбоку припеку | |
| Противоположно направленные векторы | Люди с базара, а Назар- на базар | |
Глава 3. Математика и поэзия
Аналогичную работу проделаем и с поэтическими произведениями: составим таблицу аналогий, приведем примеры стихотворных строк, где упоминаются математические объекты. Поэты не пытались написать нечто математическое, они описывали совсем другое. А мы попытались связать написанные ими произведения с математическим материалом.
Поэтические строки в математике
| Поэтический объект | Математический объект |
| В песчаных степях аравийской земли Три гордые пальмы высоко росли. Родник между ними из почвы бесплодной, Журча, пробивался волною холодной. М. Ю. Лермонтов. Три пальмы | Центр вписанной или описанной окружности в треугольнике |
| Начинают строительство с колышка, Что вбиваем мы в это полюшко. После в линии, как в тетрадке, Ровно вписываем палатки. И. Донич | Алгоритм построения треугольника, вписанного в окружность |
| Три мудреца Три мудреца в одном тазу Пустились по морю в грозу. Будь попрочнее старый таз, Длиннее был бы мои рассказ. С. Маршак | Обратная пропорциональность |
| Дни растущие, а ночи – Что ни сутки, то короче. С. Маршак, Радуга-дуга | Убывающая функция, обратная пропорциональность |
| ...А вы, друзья, Как ни садитесь, Все в музыканты не годитесь. И. А. Крылов | От перестановки мест слагаемых сумма не изменяется |
| Снег на крыше, на крылечке. Солнце в небе голубом. В нашем доме топят печки, В небо дым идет столбом. С. Маршак. Круглый год | Перпендикуляр к плоскости (дым перпендикулярен плоскости неба и земли) |
| Вот в одинаковых платьях, как сестры, Бабочки сели в траву отдыхать. То закрываются книжечкой пестрой, То, раскрываясь, несутся опять. С. Маршак. Разноцветная книга | Подобные фигуры |
| Видели люди, смотревшие снизу, Как осторожно он шел по карнизу. Вот он прошел половину пути. Надо еще половину пройти. С. Маршак. Рассказ о настоящем герое | Середина отрезка |
| Однажды Лебедь, Рак да Щука Везти с поклажей воз взялись, И вместе трое все в него впряглись, Из кожи лезут вон, а возу все нет ходу! И. А. Крылов | Некомпланарные векторы, сумма векторов (равнодействующая сил, действующих на воз, равна нулю) |
| Там, за синими курганами, На распутье трех дорог, Убаюканный туманами, Спит зеленый хуторок. И. Приблудный | Начало координат (распутье трех дорог точка пересечения трех координатных осей) |
| Упрощаюсь, словно очищаюсь От всего, что нажито тщетой. Вновь с душою легкой просыпаюсь, Точно в праздник или выходной! А. Кравченко | Упрощение выражений |
| У лукоморья дуб зеленый, Златая цепь на дубе том, И днем и ночью кот ученый Все ходит по цепи кругом. А.С.Пушкин | Эвольвента круга (линия, которую описывает при движении кот) |
| Не дорога, серпантин: Снизу-вверх, ну а сверху –вниз. А.Кравченко | Синусоида (косинусоида) |
| Судьба, как ракета, летит по параболе Обычно - во мраке и реже – по радуге... Идут, к своим правдам по-разному храбро, Червяк - через щель, человек – по параболе... Сменяя каноны, прогнозы, параграфы, Несется искусство, любовь и историяПо параболической траектории. А. Вознесенский | Парабола |