Научно-исследовательская работа«Производная в жизни человека»Авторы: Руководитель: Андреева Н.В.с. Красноармейское2015СодержаниеI.Введение.II.История производной.III.Понятие производной.1.; Определение производной;2. Геометрический смысл производной;3. Физический смысл производной4. Алгоритм вычисления производной;5. Связь свойств функции и ее производной.IV. Приложения производной.

1. 
   Скорость и ускорение;
   
2. 
   Производная в физике;
   
3. 
   Задачи на максимум и минимум;
   
4. 
   Применение производной в химии и биологии;
   
5. 
   Применение производной в экономике;
   
6. 
   Производная в электротехнике;
   
7. 
   Производная в географии.
   

V. Заключение.СОДЕРЖАНИЕ1. ВведениеПри изучении раздела «Производная» ученики нашего класса задали вопрос «Зачем нужна нам производная?» Учитель ответил: «Еще вы не знаете как необходимо знание производной. Например: в физике, химии, биологии, географии, экономике и т.д.»И мы решил подробнее изучить материал по данному вопросу. Оказалось, что на уроках мы узнали мало, а вопрос очень обширный. Самостоятельно и дополнительно решили изучить основы дифференциального исчисления, которые способствуют осознанному качественному усвоению материала, развитию правильного представления об изучаемом понятии, его огромной значимости в различных областях. В ходе работы мы пытались доказать поставленную задачу. Пришли к тому, что производная функции играет важную роль в естественно-научных и инженерно-технических исследованиях. Для многих отраслей науки она стала важным орудием количественного расчета, методом точного исследования и средством предельно четкой формулировки понятий и проблемАктуальность темы заключается в том, что человек в повседневной деятельности постоянно сталкивается с решением задач на оптимизацию, которые могут быть полностью описаны с помощью функций на математическом языке. Например, ученик живет далеко от школы и может добраться до школы на автобусе за 30 мин. или же часть пути проехать на автобусе, а потом на троллейбусе и затратить 20 мин. Рассмотрим решения. Второе решение будет лучшим, если требуется попасть в школу за минимальное время, т.е. оно лучшее по критерию минимализации времени. По другому критерию (минимализации стоимости или минимализации числа пересадок) лучшим является первое решение. В работе исследуются оптимизационные задачи. Применение производных является мощным орудием исследования функций. Эта тема является одним из основных разделов начал математического анализа. При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов, которую и решают с помощью производной.

---

В исторических данных формула производной встречается ещё в 15 веке. Великий итальянский математик Тартальи, рассматривая и развивая вопрос - на сколько зависит дальность полёта снаряда от наклона орудия - применяет её в своих трудах. Метод дифференциального исчисления был описан в XVII и XVIII вв. И. Ньютоном и Г.В. Лейбницем. Они пришли к открытию дифференциального исчисления при решении задач о скорости движения материальной точки в данный момент времени и проведении касательной к произвольной линии, объяснив этим ее геометрический смысл. Производная и различные изложения с её применением стали встречаться в работах Галилео Галилея, Декарта, французского математика Роберваля и англичанина Грегори, Большой вклад по изучению производной внесли такие умы, как Лопиталь, Бернулли, Лангранж и др.Дифференциальное исчисление широко применимо в настоящее время, например, в экономическом анализе. Они помогают точно вывести данные об изменении экономики государства. Используя их, можно совершенно точно просчитать, как можно увеличить доход государства и за счёт чего он может быть увеличен. Формула позволяет увидеть планируемые действия, понять их необходимость, тем самым, помогая экономистам в составлении успешных бизнес-планов.Дифференциальное исчисление - это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники

• 
  математики;
  

Элементом новизны в моей работе является изучение дополнительного материала по теме. Применение понятие производной в области науки и техники и в жизни человека.Методы исследования:1.Работа по школьному учебнику;2. Поиск, сбор, анализ материалов;3. Посещение в ЗАГС по вопросу сбора материала для изучения идеи социологической модели Томаса Мальтуса 4. Использование поисковой системы в пространстве Интернет;Этапы выполнения работы:

№	Название этапа	Содержание этапа
1	Подготовительный	Выбор темы, первоначальный подбор материалов
2	Основной этап	Анализ и отбор собранной информации, распределение материала по этапам работы, обобщение, создание мультимедиа-презентацию
3	Заключительный этап	Защита работы, выступления на уроке математики, декаде математики, информатики и физики, участие на научно- исследовательских конференциях в сопровождении мультимедийной презентации.

---

Структура и объём работы. Структура работы обусловлена целью и задачами исследования. Она состоит из введения, основной части, заключения, библиографического списка. Практическое значение работы. Работу можно использовать при изучении курса «Математика» на уроках математики (защита рефератов), при проведении внеклассных мероприятий. Ожидаемый результат:- приобщение подрастающего поколения к историческому прошлому;- будет способствовать воспитанию национальной гордости, чувства любви к малой родине;2. Основное содержаниеЦель работы: Исследование роли производной в науке и техники, возможности конструировать по реальным событиям математической модели и решать важные задачиЗадачи:- собрать, изучить и систематизировать материал о производной;- рассмотреть, как производная используется при решении практических задач;- использование производной в различных сферах жизнедеятельности. I. Понятие производной1. Определение производнойМатематический анализ, созданный Ньютоном и Лейбницем, долго развивался на основе интуитивного понятия производной как «скорости изменения функции». Современное определение про­изводной появилось лишь в XIX в. после того, как были уточнены основные понятия математического анализа: вещественное число, функция, предел. 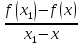С их помощью можно дать следующее определение:Производной функцииy = f(х) называется предел отношения при стремлении x₁ к x.Исторически сложилась символика для обозначения участвую­щих в этом определении выражений. Разность значений аргу­мента обозначают ∆х (дельта икс) и называют приращением аргумента, а разность значений функций обозначают

---

∆у и назы­вают приращением функции.Иначе говоря, x₁ – x = ∆х, а f(x+∆х)-f(x)= ∆y.Средняя скорость изменения функции записывается как 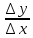. Стягивание отрезка в точку означает стремле­ние ∆х к нулю. Производную функцииy=f(x) обозначают с по­мощью штриха: у' или f '. 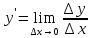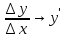Получается новый вариант определения производной:Производной функции называется предел отношения прираще­ния функции к приращению аргумента, когда приращение аргу­мента стремится к нулю.Символически определение производной можно записать так:или при 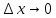2. Геометрический смысл производнойЧесть открытия основных законов математического анализа наравне с Ньютоном принадлежит немецкому математику Г. Лейб­ницу. К этим законам Лейбниц пришел, решая задачу проведе­ния касательной к произвольной кривой.Точно объяснить, что такое касательная, не­просто. Для этого по­надобится предельный переход.Пусть кривая является графиком функции y=f(x), а точка A, лежащая на графике, задана своими координатами (х; у). Касатель­ная является некоторой прямой, проходящей через точку A. Что­бы построить эту прямую, достаточно найти ее угловой коэффици­ент. Обозначим угловой коэффициент касательной k . Сначала най­дем угловой коэффициент k₁ секущей AM. Пусть абсцисса точки M равна х1.

---

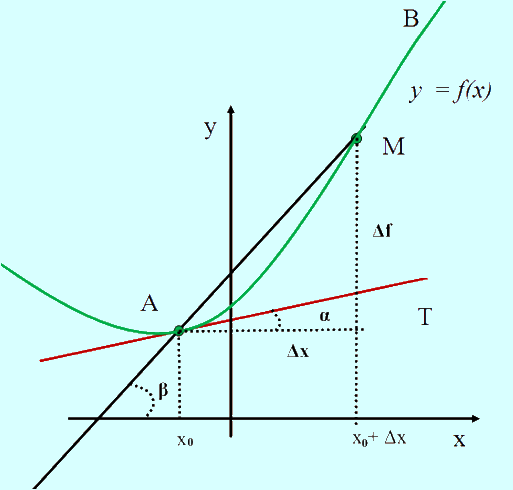
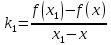
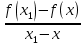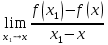
Из рисунка видно, чтоДля нахождения k надо устремить х₁ к x, Тогда точка M нач­нет приближаться к точкеA, а секущаяAM— к касательной в точке A. Таким образом, угловой коэффициент касательнойможно найти как предел выражения - при стремлении x₁ к хили в символической записи:k(x) = Этот предельный переход носит название дифференцирования функции f.2. Физический смысл производнойПредставим себе, что мы отправляемся в автомобильную поездку. Садясь в машину, посмотрим на счетчик километража. Теперь в любой момент времени мы сможем определить путь, пройденный машиной. Скорость движения мы узнаем по спидометру. Таким образом, с нашим движением (как и с движением любой материальной точки) связаны две величины — путь s и скоростьv, которые являются функциями времени t.Ясно, что путь и скорость связаны между собой. В конце XVII в. великий английский ученый Исаак Ньютон открыл общий способ описания этой связи. Открытие Ньютона стало поворотным пунктом в истории естествознания. Оказалось, что связь между количественными характеристиками самых различ­ных процессов, исследуемых физикой, химией, биологией, техни­ческими науками, аналогична связи между путем и скоростью.Основными математическими понятиями, выражающими эту связь, являются производная и интеграл. Как мы убедимся в дальнейшем, скорость — это производная пути, а путь — это ин­теграл от скорости.Построенная Ньютоном модель механического движения остается самым важным и простым источником математического анализа, изучающего

---

Смотрите также файлы

• Этапы разработки программного обеспечения. Стадия Техническое задание.docx

• Брак и семья общее и различное.pptx

• Закон рф от 29 ноября 2010 года 326 фз регулирует отношения в сфере обязательного медицинского страхования добровольного медицинского страхования обязательного и добровольного медицинского страхования.docx

• Салимсолтанова Лейла Бийсолтановна Место работы мбоу сош 60 им. И. Д. Шугаибова общая информация по уроку класс укажите класс, к которому относится урок.docx

• Программа профессиональной переподготовки финансовый директор курс управление инвестициями в реальные активы.pdf