Файл: Исследовательская работа Производная в жизни человека Авторы Андреева Н. В. с. Красноармейское 2015 Содержание I. Введение. Ii. История производной.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 237
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
производную и ее свойства. Вот почему на вопрос, что такое производная, короче всего ответить так:
Попробуйте объяснить, что такое скорость равномерного движения и как ее можно измерить. Разберемся в том, что же такое скорость произвольного движения. Пусть точка движется по прямой. Мы считаем, что нам задан закон, по которому можно вычислить путь s как функцию времени t.
Например, если точка движется под действием силы тяжести
с нулевой начальной скоростью, то s=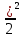 .
.
(Мы считаем, что g — ускорение силы тяжести — постоянно.)
Возможны и другие законы движения. Так, ракета, стартовавшая с поверхности Земли вертикально вверх с начальной скоростью, позволяющей полностью преодолеть земное притяжение (так называемой второй космической скоростью), удаляется от центра Земли по закону s=A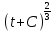 , где А и С—некоторые константы.
, где А и С—некоторые константы.
Рассмотрим отрезок времени [t1;t2]. Определим среднюю скорость точки на отрезке [t1;t2], как отношение пройденного пути к продолжительности движения:
Uср. =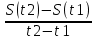
Для определения скорости точки в момент времени t
(ее в механике часто называют мгновенной скоростью) поступим так: возьмем отрезок времени [t;t1], вычислим среднюю скорость на этом отрезке и начнем уменьшать отрезок [t;t1], приближая t1 к t.
Мы заметим, что значение средней скорости при приближении t1 к t будет приближаться к некоторому числу, которое и считается значением скорости в момент времени t.
В качестве примера рассмотрим свободное падение тела. Считаем известным, что зависимость пути от времени задается функцией s= . Зафиксируем произвольный момент времени [t;t1] и вычислим среднюю скорость на отрезке:
. Зафиксируем произвольный момент времени [t;t1] и вычислим среднюю скорость на отрезке:
Ucр.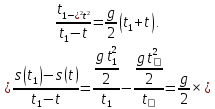
Если теперь будем стягивать отрезок [t;t1] к точке t, т.е. будем брать значение t1 все ближе и ближе к t, то сумма t1+ t будет приближаться к t + t = 2t, а выражение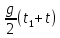 будет приближаться к
будет приближаться к 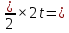 , последнее число и является значением мгновенной скорости в точке t. Мы получим хорошо известную формулу скорости
, последнее число и является значением мгновенной скорости в точке t. Мы получим хорошо известную формулу скорости
U = gt. Процедура, подобная переходу от средней скорости на отрезке [t;t1] к мгновенной скорости в точке t при стягивании отрезка в точку t, носит название предельного перехода. Обычно говорят, что при стремлении t1 к t выражение
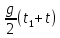
стремится к gt, и записывают это следующим образом:
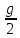 (t1 + t)
(t1 + t) 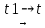 gt, или
gt, или 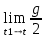 (t1 + t) = gt
(t1 + t) = gt
Используя слово «предел», можно сказать, что мгновенная скорость в точке t — это предел средней скорости при стягивании отрезка, на котором она измеряется, в точку t или в символической записи
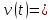
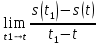
Дифференцирование, или нахождение производной,— это новая математическая операция, имеющая тот же смысл, что в механике нахождение скорости, а в геометрии вычисление углового коэффициента касательной.
Для нахождения значения производной в данной точке надо рассмотреть маленький участок изменения аргумента вблизи этой точки. Производная будет приближенно равна средней скорости на этом участке (на языке механики) или угловому коэффициенту секущей (на языке геометрии). Для точного вычисления производной надо совершить предельный переход — стянуть отрезок изменения аргумента в точку. Тогда средняя скорость превратится в мгновенную, а секущая — в касательную, и мы вычислим производную.
4. Алгоритм вычисления производной
Вычисление производной функции y=f(x) производится по следующей схеме:
1) Находим приращение функции на отрезке [x;x+∆x]:
∆y = f (х +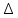 х) - f (х).
х) - f (х).
2) Делим приращение функции на приращение аргумента:
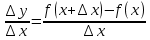
3) Находим предел , устремляя ∆х к нулю.
, устремляя ∆х к нулю.
Примеры.
а) у = С — постоянная функция.
∆y=C-C=0; = 0
= 0
Следовательно: С΄ = 0
б) у =aх+b линейная функция.
∆y=a(x+∆x)+b-(ax+b)=a∆x;
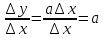
Тогда: (ax+b) '=a
∆y=a(x+∆x)2- ax2=ax2+2ax∆x+a(∆x)2- ax2=2ax∆x+a(∆x)2;
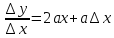 ;
;
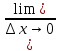
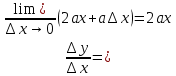 ;
;
Имеем: (ax2) '=2ax.
5. Связь свойств функции и ее производной
Важной является задача построения графика функции по ее известным свойствам.
Два важнейших свойства функции, необходимые для построения ее графика, - промежутки монотонности и точки экстремума – определяются с помощью производной. Для построения графика функции обычно сначала исследуют свойства этой функции с
Попробуйте объяснить, что такое скорость равномерного движения и как ее можно измерить. Разберемся в том, что же такое скорость произвольного движения. Пусть точка движется по прямой. Мы считаем, что нам задан закон, по которому можно вычислить путь s как функцию времени t.
Например, если точка движется под действием силы тяжести
с нулевой начальной скоростью, то s=
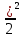 .
.(Мы считаем, что g — ускорение силы тяжести — постоянно.)
Возможны и другие законы движения. Так, ракета, стартовавшая с поверхности Земли вертикально вверх с начальной скоростью, позволяющей полностью преодолеть земное притяжение (так называемой второй космической скоростью), удаляется от центра Земли по закону s=A
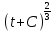 , где А и С—некоторые константы.
, где А и С—некоторые константы.Рассмотрим отрезок времени [t1;t2]. Определим среднюю скорость точки на отрезке [t1;t2], как отношение пройденного пути к продолжительности движения:
Uср. =
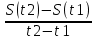
Для определения скорости точки в момент времени t
(ее в механике часто называют мгновенной скоростью) поступим так: возьмем отрезок времени [t;t1], вычислим среднюю скорость на этом отрезке и начнем уменьшать отрезок [t;t1], приближая t1 к t.
Мы заметим, что значение средней скорости при приближении t1 к t будет приближаться к некоторому числу, которое и считается значением скорости в момент времени t.
В качестве примера рассмотрим свободное падение тела. Считаем известным, что зависимость пути от времени задается функцией s=
 . Зафиксируем произвольный момент времени [t;t1] и вычислим среднюю скорость на отрезке:
. Зафиксируем произвольный момент времени [t;t1] и вычислим среднюю скорость на отрезке:Ucр.
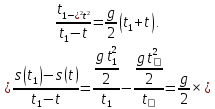
Если теперь будем стягивать отрезок [t;t1] к точке t, т.е. будем брать значение t1 все ближе и ближе к t, то сумма t1+ t будет приближаться к t + t = 2t, а выражение
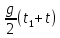 будет приближаться к
будет приближаться к 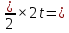 , последнее число и является значением мгновенной скорости в точке t. Мы получим хорошо известную формулу скорости
, последнее число и является значением мгновенной скорости в точке t. Мы получим хорошо известную формулу скорости U = gt. Процедура, подобная переходу от средней скорости на отрезке [t;t1] к мгновенной скорости в точке t при стягивании отрезка в точку t, носит название предельного перехода. Обычно говорят, что при стремлении t1 к t выражение
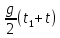
стремится к gt, и записывают это следующим образом:
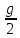 (t1 + t)
(t1 + t) 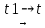 gt, или
gt, или 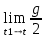 (t1 + t) = gt
(t1 + t) = gtИспользуя слово «предел», можно сказать, что мгновенная скорость в точке t — это предел средней скорости при стягивании отрезка, на котором она измеряется, в точку t или в символической записи
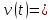
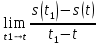
Дифференцирование, или нахождение производной,— это новая математическая операция, имеющая тот же смысл, что в механике нахождение скорости, а в геометрии вычисление углового коэффициента касательной.
Для нахождения значения производной в данной точке надо рассмотреть маленький участок изменения аргумента вблизи этой точки. Производная будет приближенно равна средней скорости на этом участке (на языке механики) или угловому коэффициенту секущей (на языке геометрии). Для точного вычисления производной надо совершить предельный переход — стянуть отрезок изменения аргумента в точку. Тогда средняя скорость превратится в мгновенную, а секущая — в касательную, и мы вычислим производную.
4. Алгоритм вычисления производной
Вычисление производной функции y=f(x) производится по следующей схеме:
1) Находим приращение функции на отрезке [x;x+∆x]:
∆y = f (х +
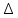 х) - f (х).
х) - f (х).2) Делим приращение функции на приращение аргумента:
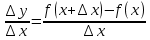
3) Находим предел
 , устремляя ∆х к нулю.
, устремляя ∆х к нулю.Примеры.
-
Производная линейной функции.
а) у = С — постоянная функция.
∆y=C-C=0;
 = 0
= 0Следовательно: С΄ = 0
б) у =aх+b линейная функция.
∆y=a(x+∆x)+b-(ax+b)=a∆x;
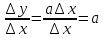
Тогда: (ax+b) '=a
-
Производная функции у =ах2.
∆y=a(x+∆x)2- ax2=ax2+2ax∆x+a(∆x)2- ax2=2ax∆x+a(∆x)2;
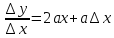 ;
; 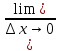
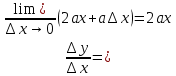 ;
; Имеем: (ax2) '=2ax.
5. Связь свойств функции и ее производной
Важной является задача построения графика функции по ее известным свойствам.
Два важнейших свойства функции, необходимые для построения ее графика, - промежутки монотонности и точки экстремума – определяются с помощью производной. Для построения графика функции обычно сначала исследуют свойства этой функции с