= N(t). Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.

Выведем формулу для вычисления численности населения на ограниченной территории в момент времени t.

Пусть у = у(t)- численность населения.

Рассмотрим прирост населения за t = t-t₀

y = k y t, где к = к_р – к_с –коэффициент прироста (к_р – коэффициент рождаемости,

к_с – коэффициент смертности)

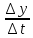= k y

При t0 получим у΄ =

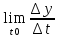
у΄= к у
7) . Применение производной в алгебре

1. Применение производной к доказательству неравенств.

Одно из простейших применений производной к доказательству неравенств основано на связи между возрастанием и убыванием функции на промежутке и знаком ее производной.

2. Применение производной в доказательстве тождеств. Доказательства тождества можно достигнуть иногда, если воспользоваться одним очевидным замечанием: Если на некотором интервале функция тождественно равна постоянной, то ее производная на этом интервале постоянно равна нулю:

3. Применение производной для упрощения алгебраических и тригонометрических выражений.

4.Разложение выражения на множители с помощью производной.

5. Применение производной в вопросах существования корней уравнений.

С помощью производной можно определить сколько решений имеет уравнение.

Основную роль здесь играют исследование функций на монотонность, нахождение

её экстремальных значений. Кроме того, используется свойство монотонных

функций:

Рассмотрим несколько примеров использование производной в жизни человека.

З а д а ч а 1. Из прямоугольного листа жести размером 25 х 40 см надо изготовит открытую коробку наибольшего объема. Для изготовления коробки надо вырезать квадратные уголки. В зависимости от длины вырезаемого квадрата получаются коробки, имеющие различные объемы. Поэтому необходимо рассчитать размеры вырезаемых квадратов, при которых коробка имеет наибольший объем.

Решение. Обозначим сторону вырезаемых по углам квадратов через х. Дном коробки является прямоугольник, стороны которого равны а = 25 – 2х и в = 40 – 2х. Высота коробки равна х. Следовательно, объем коробки равен V = (25 – 2х)(40 – 2х)х, т.е. является функцией от переменной х.

---

у = (25 – 2х)(40 – 2х)х = 4х³ – 130х² + 1000х.

Область определения этой функции промежуток (0; 12,5).

Найдем экстремумы этой функции.

у' = (4х³ – 130х² + 1000х)' = 12х² – 260х + 1000

12х² – 260х + 1000 = 0

Критические точки функции х₁  16,7 – не входит в область определения функции.

х₂ = 5

Определим знак производной в промежутках

(0; 5) у' > 0
(5; 12,5) у' < 0

Так как при переходе через точку х = 5 производная меняет знак с плюса на минус, то при

х = 5 функция у = (25 – 2х)(40 – 2х)х = 4х³ – 130х² + 1000х имеет максимум.

Следовательно, коробка будет иметь наибольший объем при вырезании квадратов со

стороной 5 см. Найдем объем полученной при этом коробки:

V(5) = 2250см³.
З а д а ч а 2. При монтаже промышленных и сельскохозяйственных зданий небольшой высоты широко используются автомобильные краны. Для правильного выбора крана необходимо знать многие исходные данные о сооружаемом объекте. В частности, габаритные данные объекта позволяют заранее определить требуемую длину стрелы крана. Рассмотрим эту задачу. Вывести формулу для определения длины стрелы автомобильного крана, с помощью которого можно построить здание высоты Н и ширины 2l c плоской крышей.Решение:Так как автомобильный кран может перемещаться вокруг всего здания, то крюк его крана достанет до любой точки здания, если он достанет до середины крыши (имеется в виду середина по ширине).



Рассмотрим кран, который находится в 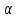точке О, подает деталь на середину крыши. Пусть угол наклона стрелы при этом составляет  . Тогда BC=  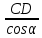= 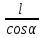; AC =  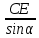= 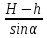, где h = АО – высота подвеса стрелы крана. В таком случае длина стрелы крана  l = +

---

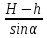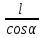
(1)

Из формулы (1) видно, что для совершения указанной работы краном, установленным в другой точке (ближе к зданию или дальше от него), потребуется кран с другой длиной стрелы, поскольку при таком перемещении меняется угол  . Определим наивыгоднейшее место установки крана, т.е. такое место, с которого заданная работа может быть выполнена краном с наименьшей длиной стрелы. 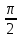Для этого достаточно определить, при каком  из промежутка (0; ) функция l принимает наименьшее значение. Найдем производную функции: l΄( ) = = ( ).

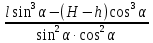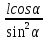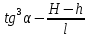Производная обращается в нуль лишь в одной точке  ₀= arctg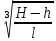 и функция l достигает своего наименьшего значения при  ₀= arctg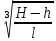 . Найдя из полученной формулы значение  ₀ и подставив его в формулу (1), мы и получим наименьшее возможное значение стрелы. Эти формулы и используются на практике.

8) Производная в строительстве

Задача 1: "Облицовка".

Заготовленной плиткой нужно облицевать 6000 кв. м боковых стенок и дна желоба прямоугольного поперечного сечения длиной 1000 м. Каковы должны быть размеры сечения, чтобы пропускная способность желоба была наибольшей?

Задача 2: "Максимальный слив"

Необходимо построить открытый желоб прямоугольного сечения для стока воды. Длина периметра поперечного сечения желоба должна равняться 6 м. Какой высоты должны быть стенки желоба, чтобы получился максимальный слив?

Задача 3: "Стоянка автомобилей".

Для стоянки машин выделили площадку прямоугольной формы, примыкающую одной стороной к стене здания. Площадку обнесли с трех сторон металлической сеткой длиной 200 м, и площадь ее при этом оказалась наибольшей. Каковы размеры площадки?

---

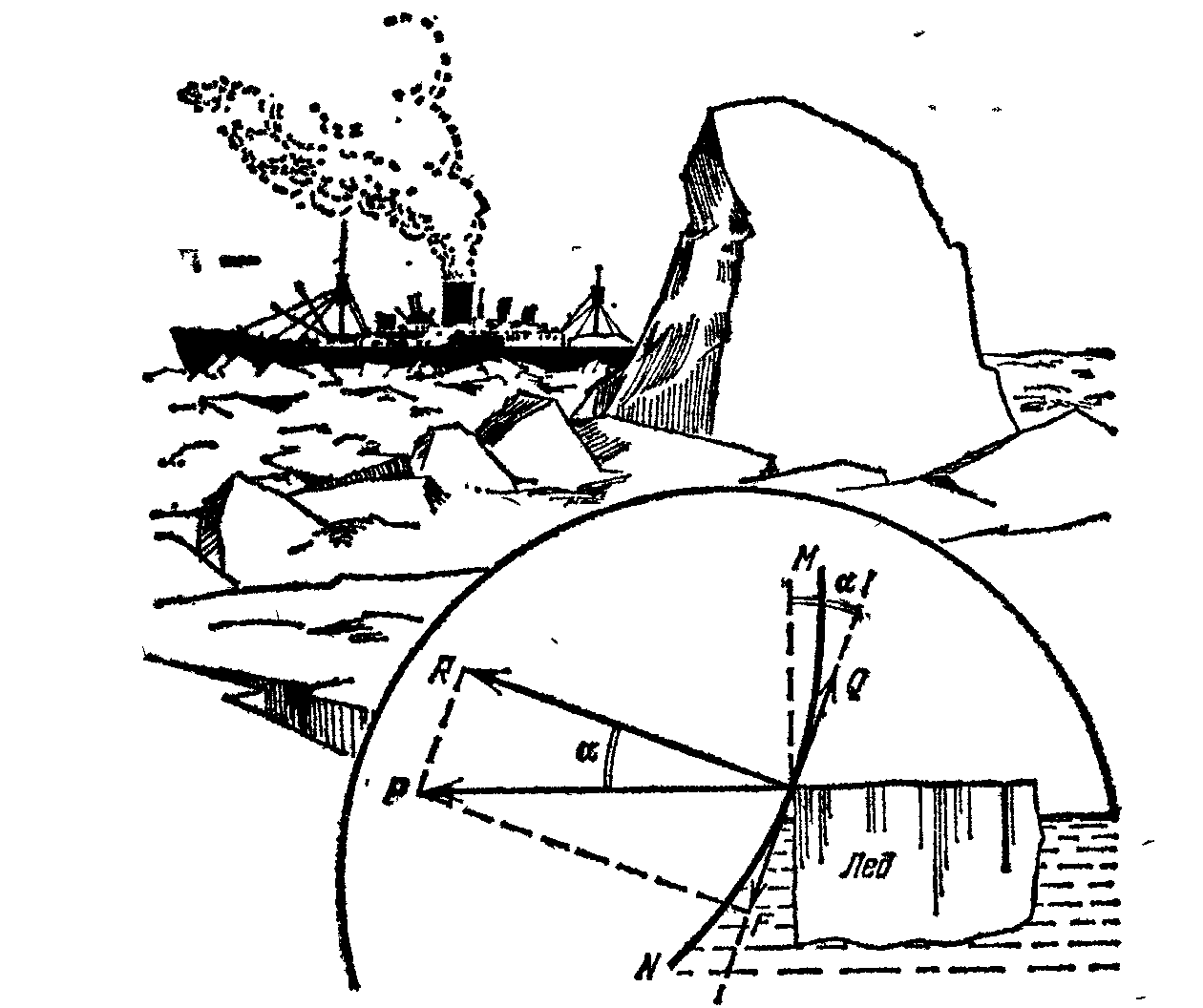
Задача 4: Пароход “Челюскин” в феврале 1934 года успешно прошел весь северный морской путь, но в Беринговом проливе оказался зажатым во льдах. Льды унесли “Челюскин” на север и раздавили.

Вот описание катастрофы: “Крепкий металл корпуса поддался не сразу, – сообщал по радио начальник экспедиции О.Ю. Шмидт. – Видно было, как льдина вдавливается в борт, и как над ней листы обшивки пучатся, изгибаясь наружу.

Лед продолжал медленное, но неотразимое наступление. Вспученные железные листы обшивки корпуса разорвались по шву. С треском летели заклепки. В одно мгновение левый борт парохода был оторван от носового трюма до кормового конца палубы…”

Почему произошла катастрофа?

Сила Р давления льда разлагается на две: F и R. R – перпендикулярна к борту, F – направлена по касательной. Угол между P и R – a – угол наклона борта к вертикали.

Q – сила трения льда о борт.

Q = 0,2 R (0,2 – коэффициент трения).

Если Q < F, то F увлекает напирающий лед под воду, лед не причиняет вреда, если Q > F, то трение мешает скольжению льдины, и лед может смять и продавить борт.

0,2R < R tg a , tg a > 0,2

Q < F, если a > 11⁰.

Наклон бортов корабля к вертикали под углом a > 11⁰ обеспечивает безопасное плавание во льдах.



Задача № 5

Высота снежка, брошенного вертикально вверх со скоростью U₀ с начальной высоты h_0, меняется по закону h =h₀+U₀*t-gt²/2, где g » 10м/c – ускорение силы тяжести. Покажите, что энергия камня Е=тv²/ 2 + mgh, где т – масса снежка, не зависит от времени.

Решение:

V (t) = h ^/ (t) = V₀ – gt

E = m/2 (V₀ - gt)² + mg(h₀ + V₀t – gt²/2) = mV₀²/2 + mgh₀
Задача 6. Количество электричества, протекающее через проводник, задаётся формулой а) q(t) = t- O t+1: б) q(t) = t+4/t. В какой момент времени ток в цепи равен нулю?

а) Решение:

I(t) = q ^/ (t),

I(t) = 1 - 1/2

1 - 1/2 =0

Отсюда, t = ? .

б) Решение:

I(t) = q ^/ (t),

I(t) = 1 - 4/t²

1 - 4/t² =0

Отсюда, t = 2 или t = -2;  t = -2 не подходит по условию задачи


V. Заключение

Этой работой мы хотели показать применение производной на примерах. Надеемся, что тема раскрыта полностью и у нас нет больше сомнений о полезности производной.

---

Данная работа помогла нам сформировать видение целостной картины информационного мира, способствовала развитию воображения, творческих способностей, побудила к

самостоятельной исследовательской деятельности, расширила круг интересов, увлекла, помогла формировать умение делать параллели и выводы. Итогом этой работы стало то, что теперь мы можем применять полученные знания на других уроках. А уроки математики перестали быть скучными и неинтересными.


Библиография
1. Алимов, Ш. А. Алгебра и начала анализа. Учеб. для 10-11 кл. сред. шк./ Ш. А. Алимов, Ю. М. Колягин, Ю.В. Сидоров и др. - М.: Просвещение, 1993.

2. Башмаков, М. И. Алгебра и начала анализа. Учеб. для 10-11 кл. сред. шк. –

М.: Просвещение, 1992.

3. Берман, Г. Н. Сборник задач по курсу математического анализа. Уч. пособие. - СПб.:

Изд-во «Профессия», 2001.

4. Задачи как средство обучения алгебре и началам анализа в X классе. Уч. пособие//

Сост. Е. С. Канин. – Киров, 1985.

5. Задачник по курсу математического анализа. Уч. пособие для студентов заочн. отделений физ.-мат. фак-тов пединститутов. Ч. I// Под ред. Н. Я. Виленкина. – М.: Просвещение, 1971.

6. Зельдович, Я. Б. Высшая математика для начинающих  и её приложения к физике.

  Уч. пособие для физико-математических средних школ и проведения факультативных занятий. – М.: Наука, 1970.

7. Колмогоров, А. Н. Алгебра и начала анализа. Учеб. для 10-11 кл. общеобразоват. учреждений/ А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др. –

М.: Просвещение, 1998.

8. М. И. Башмаков Алгебра и начала анализа. Учебник для 10-11 классов средней школы- М.: Просвещение, 1992.

9. Журнал “Математика в школе” № 6 – 1980 г. Статья “ Применение производной в практической деятельности”, автор В.Е. Львов.

10. Книга для учителя “Прикладные задачи по алгебре”, М: “ Просвещение” – 1999 г., автор

Ю.Ф.Фоминых.

11. portfolio.1september.ru

12. http://festival.1september.ru/

---

Смотрите также файлы

• Этапы разработки программного обеспечения. Стадия Техническое задание.docx

• Брак и семья общее и различное.pptx

• Закон рф от 29 ноября 2010 года 326 фз регулирует отношения в сфере обязательного медицинского страхования добровольного медицинского страхования обязательного и добровольного медицинского страхования.docx

• Салимсолтанова Лейла Бийсолтановна Место работы мбоу сош 60 им. И. Д. Шугаибова общая информация по уроку класс укажите класс, к которому относится урок.docx

• Программа профессиональной переподготовки финансовый директор курс управление инвестициями в реальные активы.pdf