4. .Экономическое приложение производной.
Экономическая интерпретация производной
В экономической теории активно используется понятия связанные с производной: 1. Предельные издержки (МС)- это издержки производства каждой дополнительной единицы продукции, они рассчитываются по формуле

Г де ТС – прирост затрат, руб.; Q- прирост выпуска изделий, ед.;

Геометрическая интерпретация предельных издержек - это тангенс угла

н аклона касательной к кривой в данной точке 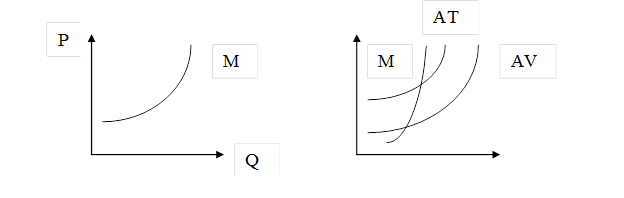(см. рис.).

Аналогичным образом могут быть определены и многие другие

экономические величины, имеющие предельный характер.

Другой пример - категория предельной выручки (MR) . Предельная выручка— это приращение общей выручки при увеличении количества выпускаемой продукции на одну единицу. MR = ΔTR : ΔQ гдеMR— предельная выручка,ΔTR— приращение общей выручки. Прибыль — это разница между выручкой и издержками.

Приведем еще один пример: Зависимость потребления индивида от дохода называется функциейсклонности к потреблению или функцией потребления.

Использование производной позволяет определить такую категорию, как предельную склонность к потреблению MPC = ΔC / ΔY ,где: ΔС - величина прироста расходов на потребление ; ΔY - величина прироста доходов домохозяйства, а предельная склонность ксбережению (MPS): MPS = ΔS / ΔY ,   
где: ΔS - величина прироста расходов на сбережение (накопление),  ΔY - величина прироста доходов домохозяйства. Поскольку, дополнительно полученные доходы идут либо на потребление, либо на сбережение, становится понятно, почему общая сумма предельной склонности к сбережению MPS и предельной склонности к потреблению MPC  всегда равна единице. То есть: MPC + MPS = 1

Аналогично, MPL - предельный продукт капитала

---

ΔТР - прирост общего продукта,

ΔL - прирост количества используемого труд

Использование производной для решения задач по экономической теории.

4. 
   Применение производной в экономике
   

Производная является мощным средством решения прикладных задач. С такими задачами в

наше время приходится иметь дело представителям самых разных специальностей:

• 
  Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;
  
• 
  Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;
  
• 
  Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.
  

З а д а ч а 1.

Предприятие производит Х единиц некоторой однородной продукции в месяц.

Установлено, что зависимость финансовых накопления предприятия от объема выпуска

выражается формулой f(x)=-0,02x³ + 600x -1000. Исследовать потенциал предприятия.

Решение:

Функция исследуется с помощью производной. Получаем, что при Х=100 функция

достигает максимума.

Вывод: финансовые накопления предприятия растут с увеличением объема

производства до 100 единиц, при х =100 они достигают максимума и объем накопления

равен 39000 денежных единиц. Дальнейший рост производства приводит к сокращению

финансовых накоплений.

---

З а д а ч а 2.

Зависимость между издержками производства y (ден. ед.) и объемом выпускаемой

продукции x (ед.) выражается функцией y = 50x – 0,05 x³. Определить средние и предельные издержки при объеме продукции, равном 10 ед.
Решение: Функция средних издержек выражается отношением: y₁ = 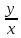= 50 – 0,05x²,

y₁(10) = 50 - 0,05•100 = 45 (ден.ед.). Функция предельных издержек выражается производной: y΄(x) = 50 – 0,15x²,
y΄(10) = 50-0,15•100 = 35 (ден. ед.).

Итак, если средние издержки на производство единицы продукции составляют 45 ден. ед., то предельные издержки, т.е. дополнительные затраты на производство дополнительной

единицы продукции при данном уровне производства, составляют 35 дн.ед.
З а д а ч а 3.

Опытным путем установлены функции спроса q= 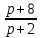и предложения s = p+0,5,

где q и s – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, p - цена товара.

Найти: а) равновесную цену, т.е. цену, при которой спрос и предложение

уравновешиваются; б) эластичность спроса и предложения для этой цены;

в) изменение дохода при увеличении цены на 5%от равновесной.

Решение:

а) Равновесная цена определяется из условия: q = s, т.е.
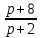= p+0,5, откуда p = 2 – равновесная цена

б) Найдем эластичность по спросу и предложению:
Ep(q) = 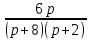; Ep(s) = 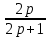. Для p = 2 имеем:
Ep=2(q) = - 0,3; Ep=2(s) = 0,8.
Таким образом, при увеличении цены p на 1% спрос уменьшится на 0,3%, а

предложение увеличится на 0,8%.

в) При увеличении цены на 5% от равновесной спрос уменьшится на 5•0,3 = 1,5%,

следовательно, доход возрастет на 3,5%.
Задача 4.

Цементный завод производит Х т. цемента в день. По договору он должен

ежедневно поставлять строительной фирме не менее 20 т. цемента.

Производственные мощности завода таковы, что выпуск цемента не может

превышать 90 т. в день.

Определить, при каком объеме производства удельные затраты будут

наибольшими (наименьшими), если функция затрат имеет вид:

---

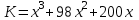. Удельные затраты составят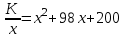

Наша задача сводится к отысканию наибольшего и наименьшего значения функции

У= х 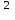+98х+200. На промежутке [20;90].

Вывод: x=49, критическая точка функции. Вычисляем значение функции на

концах промежутках и в критической точке.

f(20)=1760 f(49)=2601 f(90)=320.

Таким образом, при выпуске 49 тонн цемента в день удельные издержки

максимальны, это экономически не выгодно, а при выпуске 90 тонн в день

минимально, следовательно можно посоветовать работать заводу на предельной

мощности и находить возможности усовершенствовать технологию, так как

дальше будет действовать закон убывающей доходности. И без реконструкции

нельзя будет увеличить выпуск продукции.

Задача 5. Предприятие производит Х единиц некоторой однородной продукции

в месяц. Установлено, что зависимость финансовых накопления предприятия от

объема выпуска выражается формулой f(x)=-0,02x^3+600x -1000. Исследовать

потенциал предприятия.

Функция исследуется с помощью производной. Получаем, что при Х=100

функция достигает максимума.

Вывод: финансовые накопления предприятия растут с увеличением объема

производства до 100 единиц, при х =100 они достигают максимума и объем

накопления равен 39000 денежных единиц. Дальнейший рост производства

приводит к сокращению финансовых накоплений.

5. 
   Применение производной в химии и биологии
   

Производная характеризует в биологии – скорость размножения колонии микроорганизмов, в химии – скорость химической реакции.

Пусть зависимость между числом особей популяции микроорганизмов у и временем t её размножения задана уравнением: у = x(t).

Пусть ∆t- промежуток времени от некоторого начального значения t до t+∆t. Тогда у + ∆у = x(t+∆t)- новое значение численности популяции, соответствующее моменту t+∆t, а ∆y + x(

---

t + ∆t )- x(t) - изменение числа особей организмов. Отношение является средней скоростью размножения или, как принято говорить, средней производительностью жизнедеятельности популяции. Вычисляя , получаем y΄ = P(t) = x΄ (t), или производительность жизнедеятельности популяции в момент времени t.

З а д а ч а 1.

Пусть популяция бактерий в момент t (с) насчитывает x(t) особей. x(t) = 3000 + 100t.²Найти скорость роста популяции:
а) в произвольный момент t,
б) в момент t = 1 c.

Решение:

P = x’(t) = 200t;

P(1) = 200 (k/с).

Ответ: 200t; 200 k/с.
Пусть дана функция p=p(t),где p-количество некоторого вещества, вступившего в химическую реакцию в момент времени t. Приращению времени ∆t будет соответствовать приращение ∆p величины p. Отношение ∆p/∆t- есть средняя скорость химической реакции за промежуток времени ∆t. Предел этого отношения при стремлении t∆ к нулю - есть скорость химической реакции в данный момент времени .

v(t) = p΄(t)

Скорость химической реакции – один из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. Например, инженерам-технологам при определении эффективности химических производств, химикам, разрабатывающим препараты для медицины и сельского хозяйства, а также врачам и агрономам, использующим эти препараты для лечения людей и для внесения их в почву. Одни реакции проходят практически мгновенно, другие идут очень медленно. В реальной жизни для решения производственных задач, в медицинской, сельскохозяйственной и химической промышленности важно знать скорости реакций химических веществ.

З а д а ч а 2.

Пусть количество вещества, вступившего в химическую реакцию задается зависимостью: р(t) = 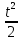+ 3t –3 (моль).
Найти скорость химической реакции через 3 секунды.

Решение:

v (t) = p΄(t);
v (t) = t + 3;
v (3) = 3+3 = 6.(моль/c)

Ответ: 6 моль/с.

6. 
   Производная в географии.
   

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t), N΄(t)

---

Смотрите также файлы

• Этапы разработки программного обеспечения. Стадия Техническое задание.docx

• Брак и семья общее и различное.pptx

• Закон рф от 29 ноября 2010 года 326 фз регулирует отношения в сфере обязательного медицинского страхования добровольного медицинского страхования обязательного и добровольного медицинского страхования.docx

• Салимсолтанова Лейла Бийсолтановна Место работы мбоу сош 60 им. И. Д. Шугаибова общая информация по уроку класс укажите класс, к которому относится урок.docx

• Программа профессиональной переподготовки финансовый директор курс управление инвестициями в реальные активы.pdf